4万5000余字详细总结锂离子电池材料计算方法

看了近100篇综述和文献总结了锂离子电池材料计算方法，涉及正极、负极、电解液等多种材料的计算和多尺度计算以及高通量计算以及材料基因组等内容。

全文约4万5000余字，为方便阅读，大家可以添加微信号（renhuangfuxilijian）或者扫描封面上的二维码添加微信免费获取PDF源文件 ，文件格式如下，含目录和所涉及到的参考文献。参考文献较多，就不在行文中标注，可见文末参考文献。PDF版本中做了详细的一一对应。

不过如下图所示，知乎貌似有字数限制，大家还是按照方法获得pdf版本吧

下文为正文：

1. 前言

1.1. 写在前面

本文主要是对目前已经公开发表的关于锂离子电池材料的计算方法进行总结，涉及到的内容从第一性原理一直覆盖到有限元以及材料基因组等多种技术。与之前发布的多尺度材料计算方法不同的是本文的主要内容是将多尺度材料计算与高通量计算方法与锂电材料的具体应用场景以及行业属性融合在一起进行撰写的。

这里需要明确的一点是，在锂电行业领域，通过计算材料学技术来提升研发效率、改进质量问题已经成为了行业龙头企业的共识，目前本文作者接触到的很多锂电行业企业都已经将计算材料学作为了其研发工作中的一环。

因此，本文基于如下条件：（1）不再讨论计算材料学是否能够应用到锂电领域；（2）核心观点是在锂电企业的哪个环节要用到计算材料学工具和相应的方法论和使用流程。

1.2. 背景介绍

新能源材料是现代科技发展的一个热点，电池材料的研究也是如火如荼。与此同时，计算机技术的发展使得第一性原理计算模拟的应用越来越广泛。用理论计算来分析电池材料的储能机理能够从原子尺度分析电化学反应动力学，结合高精度的实验表征技术往往可以很好地阐释结构和性能之间的关系。理论计算也可以用来预测电极材料的电化学性能，或者在大量的材料中筛选合适的电极材料，而不需要繁复的实验和仪器表征。用理论计算来指导实验往往能节约时间和成本。

图1 锂离子电池研究过程中空间尺度的跨度

1.3. 方法分类

目前针对对于锂离子电池材料的计算方法主要分为如下几类：（1）多尺度计算方法，包括第一性原理、分子动力学、计算相图、相场、蒙特卡洛、分子力场以及有限元等方法；（2）热力学方法和动力学方法。在Meng等人的著作中将第一性原理用于锂电材料的计算技术分为两类：（1）热力学方法；（2）动力学方法。

其中热力学方法主要包括：（1）平衡电压；（2）电压曲线；（3）电子结构；（4）稳定性分析。其中稳定性分析，还包括：（1）0K相稳定；（2）表面稳定性；（3）电极电解液界面稳定性；（4）缺陷和掺杂。

对于动力学方法其情况如下文所述。有两种广泛使用的第一性方法可以评估电池材料中碱离子扩散的动力学：基于过渡态理论的方法，例如微动弹性带方法和从头算分子动力学模拟。接下来，我们将介绍离子扩散研究的每种方法的关键概念及其局限性。动力学方法包括：（1）过渡态理论；（2）第一性原理分子动力学理论。

2. 原子尺度的模拟

材料微观尺度的计算模拟依赖于理论模型对电子、原子之间相互作用势的描述。根据势函数模型中涉及到的参数数量及类型，可分为经验模型、半经验模型及量子力学模型。依赖的经验参数越少，模型对体系的描述约接近实际，理论可有效描述的范围也越广。

近年来，第一性原理计算，特别是基于密度泛函理论的第一性原理计算同分子动力学、蒙特卡洛方法相结合，在材料设计、合成、模拟计算和评价诸多方面有许多突破性的进展，已经成为原子尺度上材料计算模拟的重要基础和核心技术。本部分将介绍第一性原理计算、分子动力学、蒙特卡洛等原子尺度的材料模拟放在在锂离子电池研究中的应用。原子尺度的模拟主要包括第一性原理、分子动力学和蒙特卡洛方法。

2.1. 密度泛函理论

密度泛函在锂离子电池基础研究中有着广泛的应用，常用于计算电极材料的结构稳定性、嵌锂电位、电子结构、能带、弛豫结构、缺陷生成能、迁移路径、活化能以及锂离子传输动力学和脱嵌锂相变等性质。针对密度泛函理论在锂离子电池材料计算中的应用，国内外已经有多个团队进行了综述。

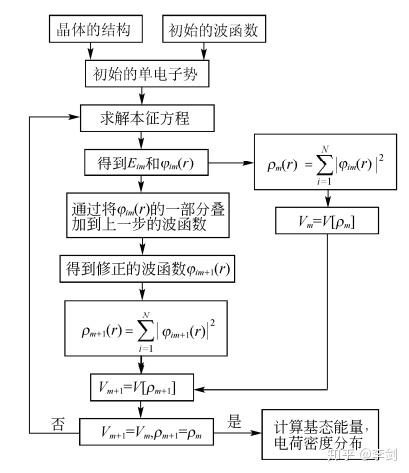
图2 密度泛函理论计算迭代过程示意图

2.1.1. 理论能量密度

基于热力学数据，根据能斯特方程，可以计算不同电化学反应体系的理论能量储存密度，从而了解化学储能体系理论能量密度的上限，了解哪些体系能够实现更高的能量密度，哪些材料具有更高的电压。

各类不同的应用对电池的各方面性能要求不尽相同，需要有针对性地开发适合的电池体系。 电池的能量密度，是最被关心的性能参数 。

电池是能够实现化学能与电能相互转换的装置。对于一个化学反应体系反应前后的化学能变化情况，可通过该反应的 Gibbs 自由能进行描述：一个化学反应在标准状态下所释放或吸收的能量，是产物的吉布斯生成能（）减去反应物的自由能，即

从式（2）～式（6）可以看出，当反应物具有较低吉布斯生成能而生成物具有较高吉布斯生成能时，电化学体系将具有较高的能量密度。对于标准状态下物质的吉布斯自由能数据可通过热力学手册查找。对于吉布斯自由能尚不清楚的物质，如果已知所有参与反应物质的晶体结构，可以通过基于第一性原理的密度泛函方法，计算出材料的吉布斯自由能；如果不知道晶体结构，也可以通过第一性原理计算先获得弛豫后的晶体结构，然后计算获得。如果已知所有材料的吉布斯生成能，当反应体系为封闭体系时，则可以计算由该反应物组成的电池按照预计反应式工作时的理论能量密度（图3）。理论电压可以通过式（4）计算，电极材料的理论储锂容量可以通过式（7）计算。

需要说明的是，上述计算中，如果反应物为气体，为了方便计算，按照反应式的摩尔计量比计算。 在实际应用中，气体来自于外界，如 O2，有些作者在计算理论能量密度时不考虑气体的质量，计算出的理论能量密度会显著高于考虑气体质量的计算方法。此外，对于固体反应物和产物来说， 由于计算采用的吉布斯生成能一般为不含缺陷的体材料（perfect bulk material）的测量数据 ，实际材料由于存在缺陷和尺寸效应，导致生成能会偏离理想材料的生成能，因此需要考虑各类缺陷能的贡献，如

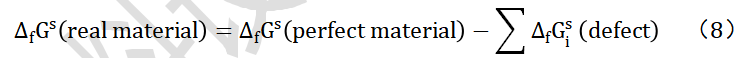
对于偏离理想情况的问题将在后续讨论中涉及。通过式（1）～式（7）可以对 1172 种较为典型的化学反应体系的理论质量能量密度、体积能量密度、电化学反应的理论电压、电极材料的理论容量进行计算。

能量密度计算的结果表明，在所有计算的封闭体系的化学储能系统中，Li/F2 体系具有 6294 Wh/kg的最高能量密度。Li/O2 体系按产物为 Li2O 计算，能量密度为 5217 Wh/kg，排名第二，如果按照产物Li2O2 计算，理论能量密度为 3500 Wh/kg。这两类电池的理论能量密度较高，是由于反应物的生成能较低，产物的生成能较高。由于氟不便于利用，因此产物为 Li2O 的 Li/O2 电池是理论能量密度最大的电池，从质量能量密度考虑，Li/O2 电池是化学储能器件的终极目标体系。

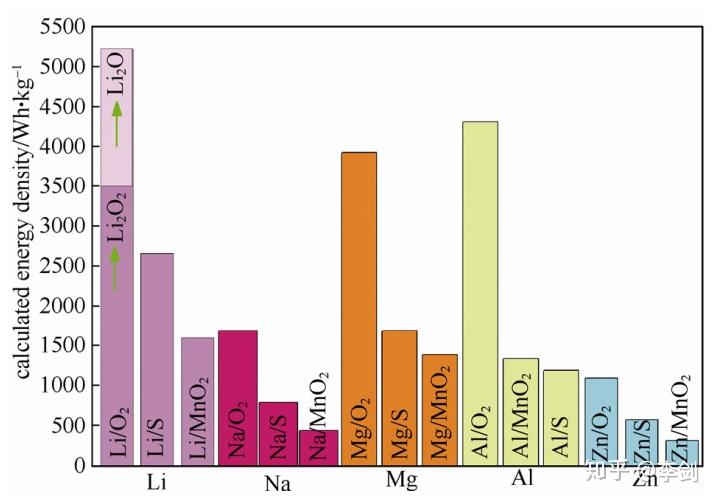
图3 不同金属负极的M/O2、M/S、M/MnO2等电池的理论质量能量密度比较

热力学理论计算有助于了解化学储能的理论极限，为估算实际电池的能量密度，开发新的电极材料、电池体系，了解化学储能器件能量密度的极限提供一定的理论参考依据。

2.1.2. 嵌锂电位

电池的电压值是与电池反应的自由能变化相关联系的参量。一个能自发进行的电化学反应，在等温可逆的条件下进行，当电池以无线小电流放电时，可对外做最大有用电功。

研究早期人们发现，几乎对所有的正极材料，密度泛函理论计算得到的电压都偏低。Zhou等认为这是由于含有3d过渡金属离子的正极材料属于强关联电子体系，其3d轨道的电子是高度局域化的。而在单电子近似的密度泛函理论框架下，局域化的电子会引入自相互作用，因此导致嵌锂电位被低估。通常对标准的GGA进行+U修正，也即GGA+U的方法，或采用杂化泛函HSE06，计算得到了与实验值更为接近的电压（图4）。在含有3d过渡金属离子的氧化物正极材料计算中强关联效应已经公认为需要考虑的效应。

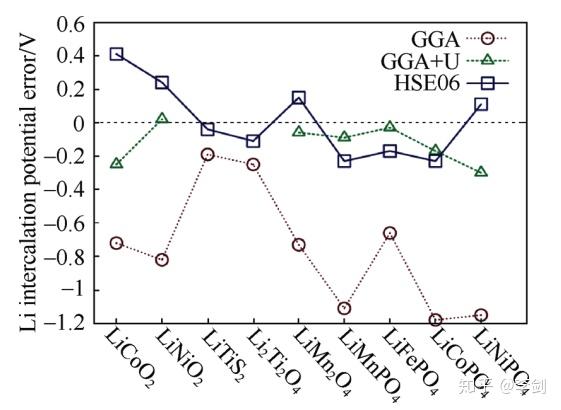
图4 标准GGA与GGA+U、HSE06计算得到各种锂离子电池电极材料嵌锂电压

2.1.3. 电极材料的稳定性

在锂离子电池材料中，目前所使用的的正极材料仍是锂源的主要提供者。若材料的主体框架在锂离子脱嵌的过程中无法稳定存在，则会导致电池性能的迅速衰减，甚至带来安全隐患，故研究电极材料的稳定性十分必要。

电池材料的结构稳定性是其能否应用的先决条件。目前报道的电池材料的计算主要采用材料的内聚能、形成能、自由能和声子频率来判断其稳定性。内聚能是指自由原子组成化合物释放的能量，内聚能越高，化合物越稳定。形成能是单质形成化合物时释放的能量，形成能越高，化合物越稳定。相比于内聚能，用形成能判断材料的稳定性更符合实际，因为实际合成材料的时候，采用的是单质，而不是单个原子。内聚能和形成能是在绝对0度下的计算结果，而吉布斯自由能可以用来判断材料在不同压强或温度下的结构稳定性。声子频率反映的是材料中原子的集体振动模式，若材料的声子谱中出现明显的虚频，说明材料不能稳定存在，然而声子谱的计算量较大，一般用来处理较小的结构模型。

电极材料的稳定性的预测主要基于材料热力学性质的计算。大量实验证据已经表明，层状正极材料LiCoO2、LiNiO2、LiMn2O4中，当锂的脱出量达到一定程度，材料会发生分解，转变为热力学上更为稳定的尖晶石相或岩盐相。

Wang等计算了LiXCoO2、LixNiO2、LixMn2O4材料在不同含Li含量下的热力学相图，阐明了这三种材料的分解机制。以LiNiO2为例，wang等计算了改材料在0K、220K、730K的Li-Ni-O2三元相图（图5）。通过分析相图中LixNiO2稳定存在的区域及分解经过的区域，认为LixNiO2的分解是通过层状向尖晶石相的放热反应和尖晶石向岩盐相的吸热反应两步来实现的。

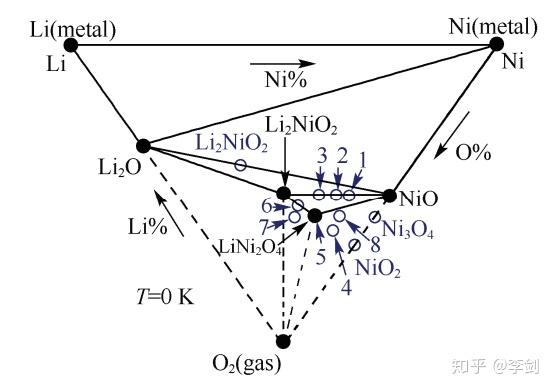
图5 计算得到的Li-Ni-O2体系在0K时的三元相图

除了脱嵌锂过程中的分解问题，电极材料在循环过程中的不稳定性还能以氧气析出的形式表现出来，这种现象在富锂相正极材料中较为常见。富锂锰基材料xLi2MnO3·（1-x）LiMO2（M=Ni、CO、Mn等）正极材料因其高容量而受到广泛的研究。然而，由于氧气释放、低的电子电导等问题导致其具有高的不可逆容量和较差的倍率性能及循环性，阻碍了该类材料在实际中的应用。Xiao等通过第一性原理计算系统地研究了富锂锰基正极材料的母相化合物Li2MnO3晶格中氧在不同锂含量时的稳定性。图6为通过第一性原理计算得到的不同脱锂态Li2-xMnO3氧气释放过程中的反应焓和吉布斯自由能。由图5可知，当脱锂量x≥0.5时会有氧气产生，进而导致结构的变化。

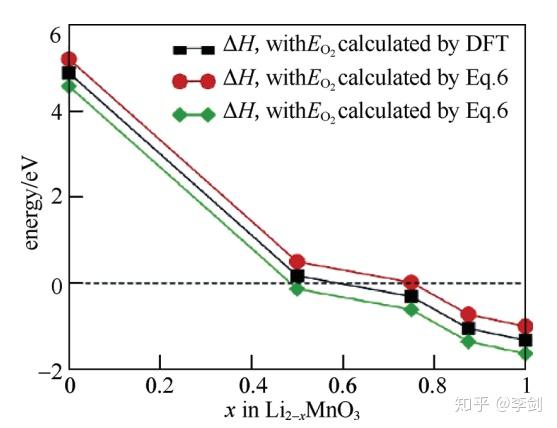
图6 计算得到的不同脱锂态Li2-xMnO3氧气释放过程中反应焓和吉布斯自由能

为改善富锂锰基材料xLi2MnO3·（1-x）LiMO2（M=Ni、CO、Mn等）正极材料充放电过程中因为氧析出导致的结构不稳定，包覆和掺杂通常成为必要的手段。理论计算方面，Gao等通过第一性原理计算了不同晶格位Mo掺杂Li2MnO3晶体的结构稳定性及Li+在晶格中不同跃迁方向的迁移势垒。图7是采用PBE+U交换关联势计算得到的不同脱锂态的LiyMnO3和LiyMn0.75Mo0.25O3的氧气释放过程中反应焓和吉布斯自由能。分析图6可知，与未掺杂的Li2MnO3相比，掺Mo的Li2MnO3结构稳定性有了大幅度提升。

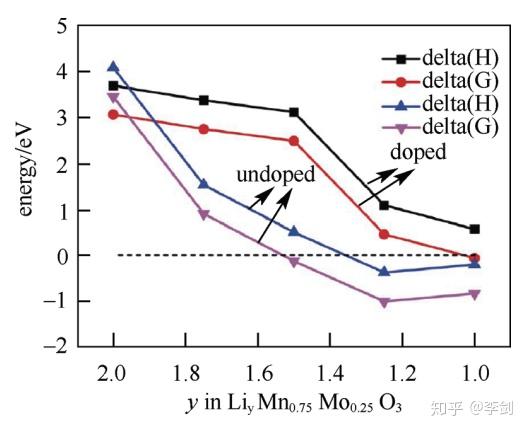
图7 计算得到的不同脱锂态LiyMnO3和LiyMn0.75Mo0.25O3的气释放过程中反应焓和吉布斯自由能

2.1.4. 电子结构

电池材料的电子结构与材料的电化学性能有着密切的关系。电极材料中脱嵌锂过程中电荷补偿的来源和氧的稳定性与过渡金属及氧的分波态密度的相对位置有关，电极与电解质界面的化学稳定性则可以从能态密度中做出定性预测，此外电池的倍率性能也与电极的电子导电性有关。电池中的固态电解质需要具有电子绝缘的特性，材料的带隙宽度与其电化学窗口的宽度有关。电极或者电解质材料的电子结构对电池的性能有重要作用。由于DFT是基于电荷密度，因此电子结构顺其自然就能得到，电子结构包含了分子轨道、能带、态密度以及电荷分布。这些性质可以帮助分析电池的性能。

电极材料的电子结构计算也出现在大量的文献报道中，它可以反应材料的稳定性、电子的转移和原子键合情况。“锂电之父”Goodenough在2010年提出，在电池中，电解质的最高占据分子轨道能级（HOMO）要低于负极材料的正极材料的费米能级，而最低未占分子轨道能级（LUMO）要高于负极材料的费米能级。否则，电解质会与正极或负极材料发生氧化还原反应，从而被消耗。因而，DFT计算可以通过对电极材料能级的计算，在理论上判断电池的设计是否合理。除了轨道能级的计算，电池材料的电子结构计算中还常采用能带结构、态密度（DOS）、差分电荷来分析材料的导电性、电子结构变化、原子间的键合情况等。

2.1.4.1. 分子轨道

用于电池的电解质材料的选择必须符合一些特定规则，例如低毒性，低成本，低电子电导率和高离子电导率以及不易燃性。良好的电池设计应避免电解液中发生化学反应。2010年，Goodenoug提出，合格的电解质应具有较大的电位窗口，其最高占据分子轨道（HOMO）低于阴极的Femi能级（μC），而最低占据分子轨道（LOMO）则高于阴极的Femi能级。阳极的费米能级（图7中的μA）。如果高于LUMO，电解质将被还原，而当μC低于HOMO时，电解质将被氧化。幸运的是，如果形成稳定的固体电解质界面（SEI）来防止电子在电极和电解质之间转移，则可以缓解此问题。DFT可用于计算候选电解质中的HOMO / LUMO能量，可用于检查电解质与特定阳极和阴极材料的相容性。

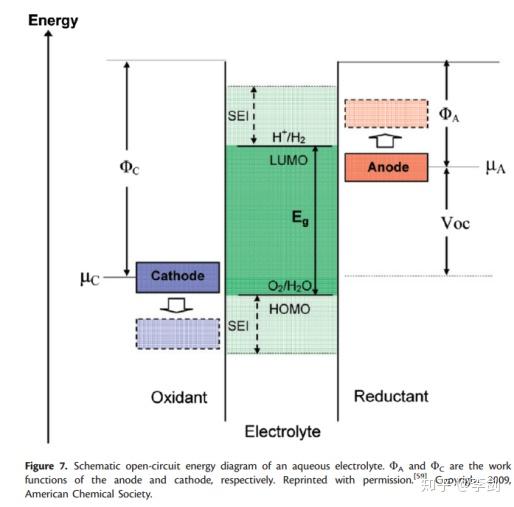
图8 Goodenough提出的示意图

2.1.4.2. 能带结构

在固态物理学中，电子能带结构提供有关固体罐中电子占据的能级范围的信息，并且带隙与电子导电性密切相关。从最近的DFT研究中，Xiong等人预测，由于Mg3N2具有稳定的结构和较高的理论容量，适当的嵌入电势以及较低的离子传输势垒，因此它是锂离子电池潜在的高性能阳极材料。图9显示了原始和锂化Mg3N2材料的DOS和能带结构。他们的计算表明，原始的Mg3N2的带隙仅为0.91 eV（PBE），表明它是半导体。在嵌入锂离子之后，中间体LiMg3N2和最终产物Li7Mg3N2是没有带隙的金属，这意味着锂化过程增强了Mg3N2的电子导电性。由于PBE官能团倾向于低估带隙，因此HSE06杂合官能团已用于重新计算带隙。正如预期的那样，Mg3N2的HSE06带隙为1.92 eV，比PBE高约1 eV。但是，锂化的Mg3N2物质即使具有HSE06功能，也已证明是金属的。基于这些电子结构分析表明，Mg3N2在循环过程中具有良好的电导率和良好的倍率容量。

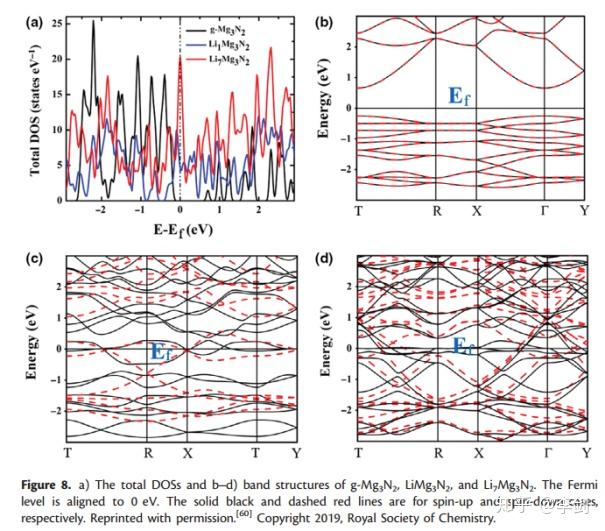
图9 DOS图

2.1.4.3. 态密度

DOS本质上是允许电子占据的特定能级上不同状态的数量，即每单位体积每单位能量的电子状态的数量。根据最近的DOS分析，Breuer等证实了在LiNi0.5Co0.2Mn0.3O2（NCM523）中掺杂Mo6 +会影响其电子结构，从而影响LiBs中的电化学性能。未掺杂和掺杂Mo的NCM523的DOS计算结果如图10所示。尽管掺杂Mo后DOS没有明显变化，但是Ni2 +部分DOS（PDOS）的增加和Ni3 + PDOS的相应减少证明了Ni3 +的电荷补偿。此外，基于计算和实验结果，接近Femi级的Mo6 +导带增加了NCM523的电导率，Mo PDOS的位置也解释了电池循环过程中Mo5 +和Mo6 +的出现。

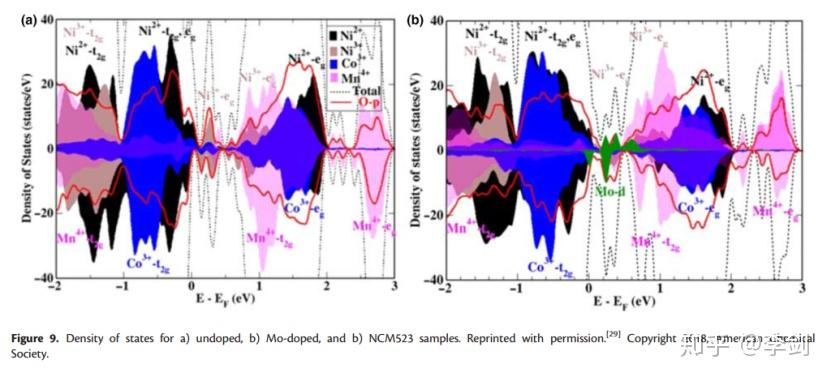
图 10 DOS图

材料的带隙直接关系到其电导率，可以使用DOS图分析电极材料的电子电阻。 Lee计算了聚合石墨碳氮化物（pgCN）和无定形炭黑（a-CB）的复合材料的DOS和它们各自的DOS。事实证明，pg-CN的带隙为2.0 eV，而a-CB和a-CB / pg-CN复合材料没有带隙。结果证明，用一层pg-CN包裹原始a-CB的策略可以增强结构稳定性，而不会降低其电子导电性。

最近，DFT已被用于新兴的研究MIB材料和Lee等人使用半局部PBE和混合HSE06功能计算了Mg3Bi2（一种具有良好倍率性能的潜在MIB阳极材料）的DOS和能带结构（图10）。PBE和HSE06的计算都表明，价带的顶部几乎完全起源于Bi 6p轨道。Bi 6s的顶部和Bi 6p的底部之间的大间隙表明Mg3Bi2的化学惰性。由于PBE通常会低估固体的带隙，因此对于有或没有自旋轨道耦合（SOC）的Mg3Bi2，PBE都不会给出带隙，而对于Mg3Bi2，HSE06会给出0.36 eV的带隙。他们的评估表明，SOC可减小带隙并增加Bi 6p的色散，在计算含重原子的体系时应考虑到这一点。

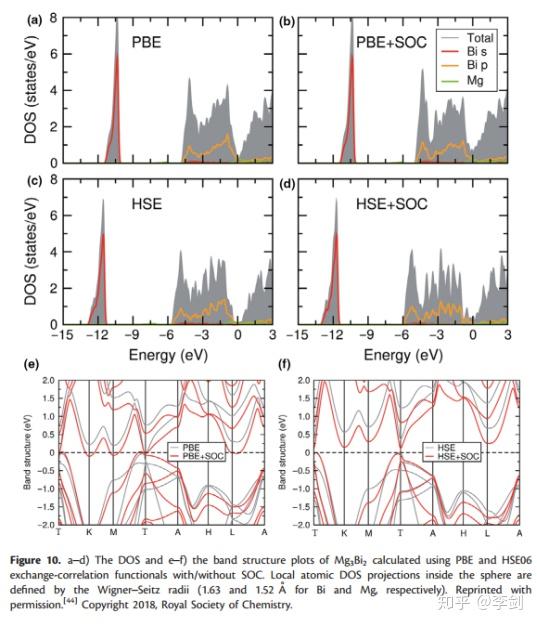
图11 DOS图

DOS可用于计算电子占据状态，并且Chakraborty等采用了SCAN meta-GGA密度功能计算层状过渡氧化物（包括LiNiO2，LiCoO2和LiMnO2）的结构，磁性和电化学性质，这是用于LiBs的商业阴极材料。在图12中对这些化合物的DOS进行了比较，结果表明Ni，Co，Mn-d和O-p状态具有独特的杂交，表明过渡金属原子与氧原子之间的牢固结合。此外，金属d态对费米能级附近的价带有重要贡献。此外，LiNiO2中的Ni3 +和LiCoO2中的Co3 +处于低自旋状态（t2g 6（|↑↓|↑↓|↑↓|），例如0（| | |）），这意味着向上和向下向下的t2g自旋通道被完全占用。相反，LiMnO2中的Mn3 +处于高自旋状态（t2g 3（|↑|↑|↑|），例如1（|↑| |））。将基于meta-GGA功能的结果与使用PBE + U和PBEfunctionals获得的结果进行了比较。从他们的比较中，我们可以看到PBE + U官能团低估了费米能级附近的金属d态的能量，而SCAN提供了更准确的预测，而PBE + U倾向于高估了O-p态的能量。

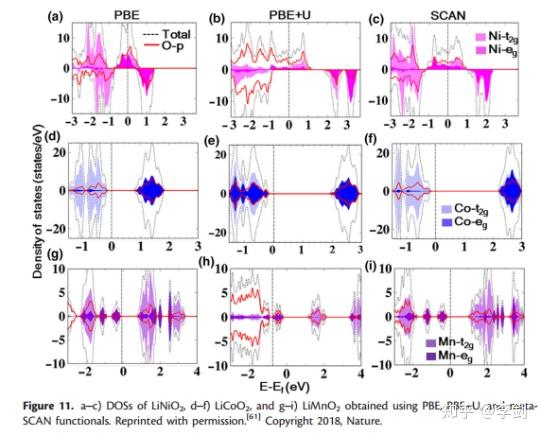
图12 DOS图

2.1.4.4. 电荷分布

显示电子结构的一种流行形式是从DFT计算获得的电子/电荷分布。电荷分布图清楚地显示出电极材料的电子结构和原子的化学环境，这很难通过实验测量。赵等模拟了片状MoSe2-SnO2界面并计算了界面的电荷密度（图13）。通过从MoSe2-SnO2界面的电荷密度中减去MoSe2和SnO2的各个电荷密度，可以计算出MoSe2-SnO2界面的电荷密度差。图12c，d示出了SnO 2吸附在MoSe 2上之后电子的转移。MoSe2表面上的原子失去电子，这些电子向O转移SnO2的原子数增加，并且表面上Se和O原子之间的电荷密度增加，这对应于Se和O之间的化学键的形成，这在图13a中也得到了证明。当电子离开原子核时，电子对原子核的约束减弱，因此电子的迁移率显着提高。因此，通过掺杂SnO2可以显着提高MoSe2的电子电导率，并且片状MoSe2-SnO2在SIBs中显示出高倍率容量。

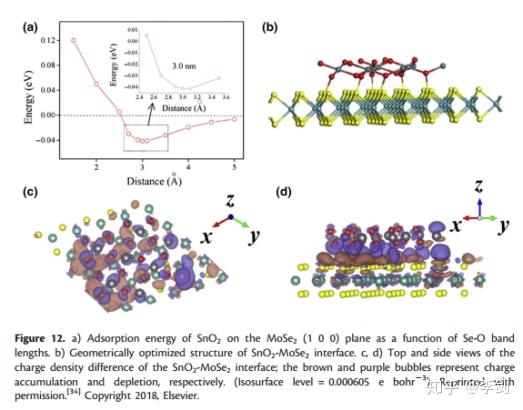
图13 MoSe2上SnO2的吸附能

最近，Wu等人报道了关于双层结构的V2O5•nH2O作为水性ZIBs阴极材料的研究，他们研究了通过电荷密度分布和DOS嵌入Zn2 +的V2O5•nH2O的电子结构。图14显示了原始和Zn2 +插入的V2O5•nH2O结构的DOS计算值和变形电荷密度。对于没有键合H2O的V2O5，大量电子从Zn转移到相邻的V和O。但是，在键合H2O的情况下，例如V2O5•H2O，电荷转移方向发生变化。除了从Zn移动到V和O外，电子主要在Zn和H2O之间交换。通过比较V2O5·H2O的DOS的变化，可以证实该结果，表明DOS在Zn2 +嵌入后移动到较低的能量区，表明Zn的电子转移到导带。为了量化转移电子的数量，作者计算了Bader电荷，结果表明，在V2O5中，V吸收了大部分源自Zn的电子，而在V2O5•H2O中，电子主要移动到H2O的氧原子上。和V2O5•1.75H2O。因此，键合的H2O对ZIBs中V2O5•nH2O的电化学性能具有重要影响。

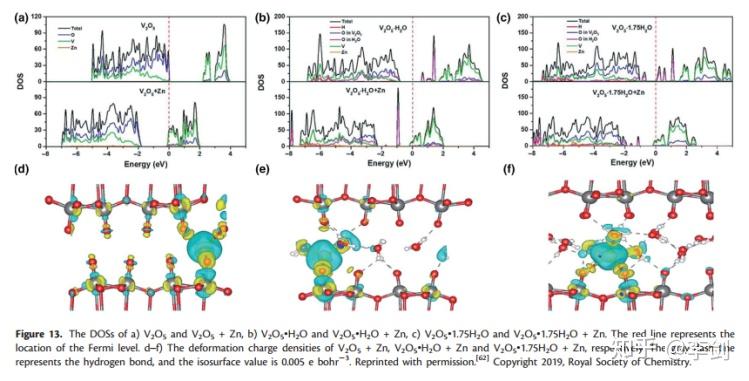
图14 DOS图与电荷密度

2.1.5. 离子输运机制与扩散系数模拟

利用计算机可以模拟锂离子的扩散运动，下面讨论锂离子扩散常采用的 蒙特卡洛法、分子动力学法和弹性能带法。

锂离子的传输是锂二次电池中核心的输运过程，锂离子传输的路径、能量势垒等与电池的倍率性能、极化强度、离子互占位等现象有着直接的联系。锂离子在材料中的扩散性质一方面可以通过基于过渡态能带理论的弹性能带方法（NEB）获得，另外也可以采用基于第一性原理的分子动力学方法计算得到。

2.1.5.1. 蒙特卡洛法

蒙特卡洛方法对锂离子在固体材料中的传输问题通常选用Metropolis算法，将把锂离子迁移过程考虑成马尔科夫（Markov）过程，锂离子每次跳跃的位置都是Markov链上的一个节点，而前一个节点到后一个节点跳跃的发生是否成功由一定概率来决定。具体研究思路包括两类：（a）利用经典相互作用进行简化，通过近似表达式计算锂离子在不同个点的位能；（b）通过第一性原理计算方法得到位能。

直接利用经典相互作用简化时，不同材料体系和不同体系的位能表达式不同，需要建立合理的位能表达式才能提高模拟结果正确性。Ouyang等计算LiMn2O4中锂离子扩散行为时，将Li+和LiMn2O4晶格中Li+与Mn和O之间的相互作用平均为一个不变的常数，并认为等于Li+在其中的化学势μ，得到每个锂离子格点的位能，可用下式表示：

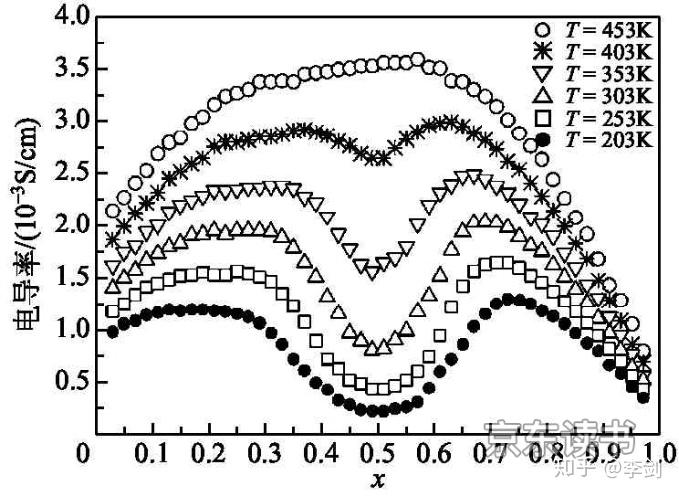
图15 不同浓度下锂离子导电性

第一性原理计算可以精确地计算一些具有代表性原子结构的能量，然后通过集团展开方法拟合出能量与结构参数的一般表达式，从而获得所有可能结构模型的能量；然后通过蒙特卡洛模拟技术模拟锂离子在各种复杂材料中的扩散和输运性质。通过第一性原理计算获得的能量表达式比经验位能模型能量要准确，同时对于结构复杂难以建立检验模型的体系，也可以比较方便地获得结构能量。Ceder小组发现了锂离子在LixCoO2中的双空位扩散机制，得到的锂离子扩散系数如图16所示。

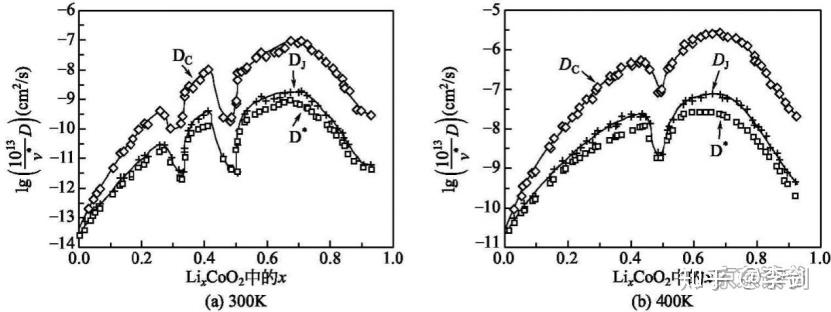
图16 LixCoO2材料中锂离子浓度与离子导电性之间关系的模拟结果

V*——指数前置因子；Dc——化学扩散系数；DJ——跳跃扩散系数；D*——原子示踪剂扩散系数

蒙特卡洛模拟优势在于模拟体系可以很大，甚至可以直接模拟真实材料大小的体系。Ouyang等在模拟LiFePO4材料中Cr对Li离子输运的阻塞效应时采用了尺寸为1000*1000*1000的晶胞，模型尺寸和实际LiFePO4材料颗粒尺寸在同一个数量级上，计算模型和阻塞见图17。另外，蒙特卡洛模拟还可以比较方便地模拟在外场作用下的离子输运。比如，在外加电场中，锂离子受到电场作用，从一个位置迁移到另外一个位置将增加一项额外电场能，而电场能可以算入迁移率Ps表达式中。这样模拟结果就代表了锂离子在外场中的迁移情况。

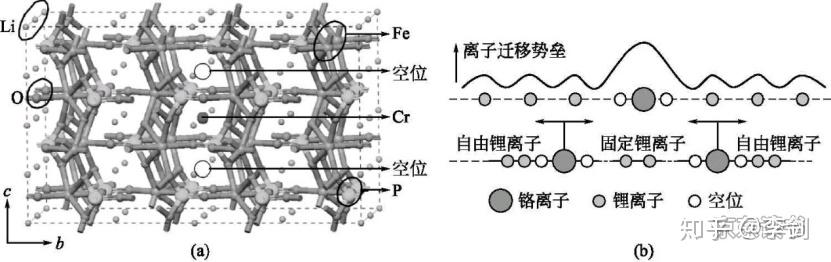
图17 LiFePO4结构模型（a）和锂离子迁移阻塞机理示意图（b）

2.1.5.2. 分子动力学方法

分子动力学方法是一种确定性模拟方法，基本思想是通过求解牛顿运动方程来描述粒子运动，在给定的势场下，已知系统中粒子初始位置和速度，可以计算出每个粒子的受力和加速度，通过求解运动方程，就可以确定粒子运动轨迹，最终可以获得每个粒子位置、速度和加速度随时间的变化。在计算锂离子扩散行为过程中，分子动力学包括经典分子动力学和第一性原理分子动力学。

经典分子动力学方法模拟受到观测时间和模拟体系大小的限制，需要引入周期性边界条件、全（漫）反射边界条件、开边界条件等边界条件。对于锂离子电池材料中锂离子扩散行为，需要计算一定温度下的扩散系数，可以选择（N，V，T）系综。应用分子动力学模拟锂离子扩散行为，最为关键的是构造出能够精确描述粒子所处势场的模型，进而计算出粒子的精确受力。对于固相材料，通常构造出精确描述粒子受力势场的模型难度很大。目前，利用经典分子动力学方法研究锂离子电池电极材料或固态电解质中锂离子输运问题的报道较少，Tateishi等构造了描述LiMn2O4材料中势场的模型，并利用该模型研究了锂离子的扩散问题，结果也不尽如人意。

第一性原理分子动力学模拟基本思想是利用第一性原理方法计算原子间受力，再通过分子动力学方法来计算原子运动，并且分开独立考虑原子运动和电子运动。利用第一性原理分子动力学模拟可以获得比较可信的结果，常用的Car Parrinello Molecular Dynamics（CPMD）法已经植入到大部分第一性原理计算软件中。利用第一性原理分子动力学方法模拟锂离子迁移，包括两种方法：选择性分析动力学法和完全分子动力学方法。选择性分子动力学方法，也称为绝热轨道近似法：某个原子沿着某个轨道从一个格点运动到另一个格点位，把整个运动过程分割成一定数目的分子动力学步数进行模拟。运动粒子的每个运动状态（每个分子动力学步），都弛豫运动原子周围的其他原子受力，同时运动原子在其运动方向的垂直平面内也进行弛豫（有些计算也可能忽略运动原子的弛豫）。这样，计算每个运动状态体系的总能量，即可获得运动粒子沿着该运动方向跃迁的迁移势垒。Meunier等计算了锂离子在碳纳米管中的扩散行为，并预测锂离子很难穿过碳六元环。Ouyang等利用同样方法计算了锂离子在LiFePO4材料中的迁移势垒，发现锂离子在该材料中的一维输运行为，即锂离子扩散只能沿着晶轴c方向进行。事实上，绝热近似方法并不是一种真正意义上的分子动力学模拟，在模拟过程中，仅有部分原子进行了迁移运动，且迁移路径也是事先给定的，模拟过程中仅仅对其他原子进行了弛豫。完全分子动力学法给出了所有原子运动轨迹及其随时间演变的信息，通过分析这些数据，可以直接获得扩散系数，该法在研究锂离子扩散行为中得到广泛应用。有研究者通过第一性原理分子动力学模拟锂离子电导率非常高的固态电解质材料Li10GeP2S12锂离子电导率在300K的温度下大约为9·10-3S/cm，与实验测量结果吻合较好。

从模拟体系大小上看，经典分子动力学能够模拟的原子数通常可以达到几千个，大规模计算可以到几十万个。第一性原理分子动力学模拟能够获得比较精确的模拟结果，但是模拟体系相对较小，原子数通常在几百个以内。从模拟时间上看，经典分子动力学通常能够模拟的时间尺度都在纳秒数量级上，有些甚至可以到微妙数量级，而第一性原理分子动力学模拟的时间尺度都在皮秒数量级上。在研究锂离子扩散时，这些限制使得第一性原理分子动力学模拟通常局限在研究扩散机理层面上，而不能真正模拟实际电池体系的扩散行为。不过，随着计算技术和计算条件提高，第一性原理分子动力学模拟在不就的将来还是有可能直接模拟实际电池体系的。

2.1.5.3. 弹性能带方法

弹性能带方法通过构造一系列迁移路径上的中间态，并优化这些中间态，达到搜索最低能量路径的目的。在优化过程中，原子受到晶体内部势能场梯度产生的力以及外加的弹性力作用。势能场产生的力使得原子从势能面上能量高的位置往能量低的位置运动，而弹性力的作用使得整个迁移路径上每个中间态之间的间距保持不变。在具体操作过程中，弹性力仅考虑投影到势能面的法线方向上的分量，从而找到每个中间态的势能面内的最低能量位置，同时保证搜索的路径不会偏离鞍点位置。弹性能带方法是对蒙特卡洛模拟和分子动力学模拟在研究和优化粒子迁移路径方面的缺陷的补充。利用蒙特卡洛模拟和分子动力学模拟得到的扩散系数，都是一定系综下的系综平均结果。而对于粒子在原子层面的某次迁移的具体路径，蒙特卡洛和分子动力学模拟都没有做更深入的考虑。虽然选择性分子动力学模拟也考虑了一定的粒子迁移路径，但对路径的优化却十分有限。对于迁移路径较为复杂的扩散行为，选择性分子动力学模拟的结果往往和实际情况相比有较大的出入。

利用弹性能带计算锂离子的迁移路径，首先要考虑的是锂离子在晶格中的稳定占位情况。从技术上来说，弹性能带计算需要给出确定的初态和终态。初态代表迁移离子在一个稳定的格点位，而终态代表锂离子在另一个格点位。因此，利用弹性能带计算来研究锂离子的扩散行为，首先必须分析清楚这些格点位有哪些，并考虑锂离子在各种格点之间的可能路径。一般而言，锂离子的迁移都是从一个稳定格点向其近邻的稳定格点迁移，因此根据稳定格点最近邻的稳定格点数目，可以预先构造出一系列迁移路径。最后，通过弹性能带计算，优化出每条路径的具体粒子迁移的轨迹和迁移势垒，具体见图18。利用弹性能带法计算锂离子在LixTi5O12电极中的扩散路径和势垒，得到的扩散系数见表1。

表1 锂离子在不同晶格的扩散势垒和扩散系数

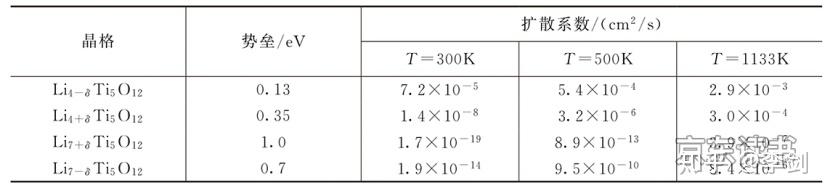
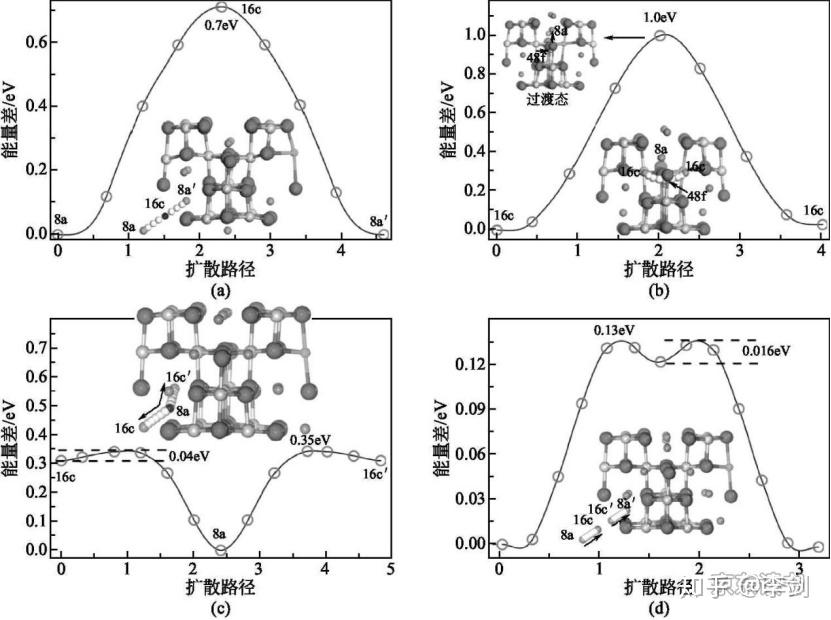
图18 锂离子在Li4-δTi5O12（a），Li4+δTi5O12（b）,Li7+δTi5O12（c），Li7-δTi5O12（d）晶格中的扩散路径和势垒

采用类似方法，人们也模拟了锂离子在LiMn2O4和SEI膜中Li2CoO3中的扩散系数。这些研究一方面可以直接得到锂离子在材料中的迁移势垒，同时还可以从原子尺度上绘制出详细的锂离子的迁移路径，对理解锂离子扩散的微观机理提供直观的物理图像。

Ouyang等通过第一性原理计算研究了锂离子在橄榄石结构的LiFePO4中的扩散机理。通过对不同的可能扩散路劲的迁移势垒的计算，表明对于LiFePO4、FePO4以及Li0.5FePO4来说，扩散势垒沿着c轴方向分别为0.6、1.2和0.5eV。而在沿着a轴、b轴方向的迁移路径上，其扩散势垒非常大，以至于锂离子难以扩散。这说明Li离子在LiFePO4中的扩散是一维的。这种一维的扩散行为通过第一性原理的分子动力学模拟得到了更进一步的验证，并且直观地观察到了锂离子的一维扩散行为。

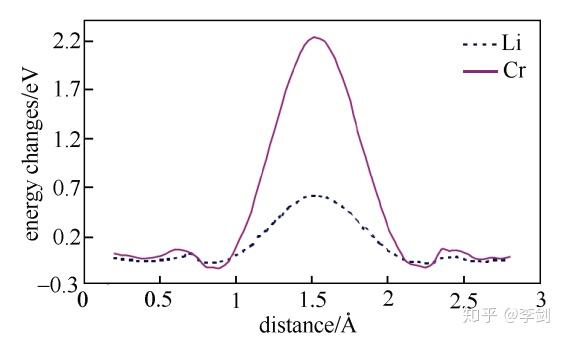
图19 Li与Cr在LiFePO4晶体中沿着c轴方向的迁移势垒

为进一步解释Cr在Li位掺杂的LiFePO4材料电子电导率得到了大幅度提高而其电化学性能没有得到明显改善的现象，ouyang等计算研究了纯的和Li位掺杂Cr的LiFePO4中锂离子和铬离子沿着一维扩散通道输运的能量势垒（图20所示分别为Li与Cr沿着C轴方向的迁移势垒），结果发现锂离子可以很容易地沿着扩散通道扩散，但是铬离子很难离开本来的位置。这意味着铬离子堵塞了材料的一维扩散通道，如图10所示。从不阻塞一维离子输运通道的角度出发，他们考虑了低价态Na+的Li位掺杂以及其它金属离子的Fe位掺杂对材料动力学性能的影响，并发现两种方法都能够不同程度地提高材料的电子电导率，且不会阻塞Li+的一维输运通道。

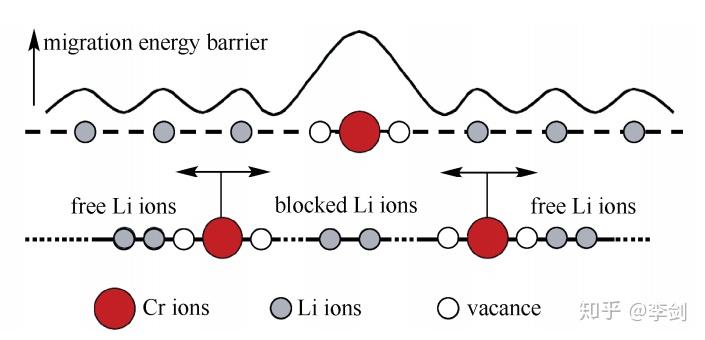
图20 Cr掺杂导致的锂离子输运阻塞效应模型

Velasquez等人报道了当LiMn2O4的纳米颗粒尺寸小于特定尺寸（~15nm）时，LMO的尺寸越小，电池性能越差。这种现象在LIB中是恰恰相反的。为了解释这种现象，采用DFT+NEB的方式来研究。计算了尖晶石结构中在不同尺寸下的能量势垒（见图21）。图14（d）中三个不同方向的Li的能量势垒揭示了相关的结果。结果显示在体相LMO中Li离子的最大扩散势垒为0.33eV，而在纳米颗粒中（图22，d）存在两条可能的Li+扩散路径，分别是0.59eV和0.72eV。DFT计算结果显示，随着尺寸从14nm到1.4nm变化，对应的能量势垒从0.33eV逐渐增加到最少0.59eV。一系列的计算结果显示随着材料尺寸的减小，为嵌锂和脱锂造成了阻碍，进而导致电压升高。

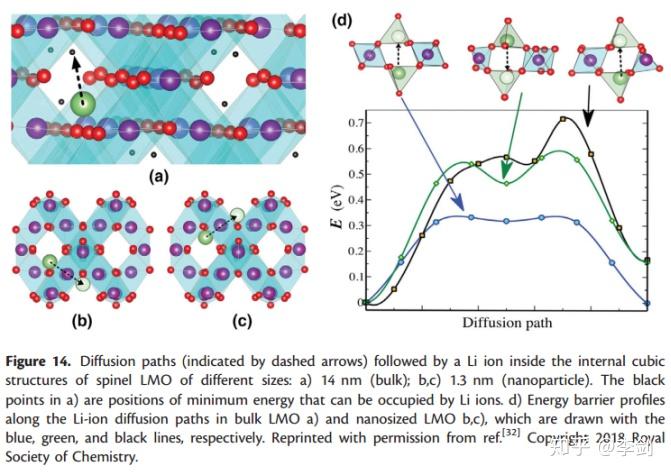
图22 扩散路径

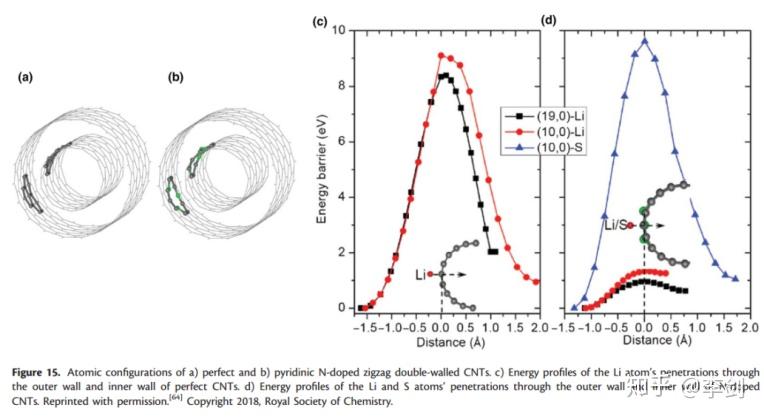
Wang等人最近研究了LSB电池中对CNT的N掺杂，比较了N掺杂CNT与本征CNT的迁移势垒。他们研究了Li+在外表面、内表面以及内部空间的扩散。对于完美的CNT，其扩散势垒分别是8.4和9.1eV，而对于N掺杂的CNT，其扩散势垒分别为0.95和1.33eV。完美CNT比N掺杂的要高。进一步分析表明是因为较高的能垒导致S原子被封装在CNT中。这也揭示了N掺杂的CNT可以作为未来潜在的高性能的LSB电池正极材料。

2.1.5.4. AIMD与NEB的比较

与经典的MD相比，AIMD中的力可以通过DFT计算获得，并且AIMD在量化扩散特性方面更为准确。 但是，AIMD需要更多的计算资源，并且如果扩散相当快，则只能处理数百个原子的系统。 NEB方法仅为迁移路径提供了能量屏障，但AIMD可以进一步提供扩散系数和离子电导率，可以通过实验验证。

2.1.6. 缺陷生成能

在锂离子电池电极与电解质材料研究中，缺陷化学对于理解材料的物理化学性质，指导材料的理性设计与优化方面具有重要的意义。锂离子电池材料中缺陷形态的类型、热力学基础、缺陷的存在对材料性质的调制等方面均有影响。如缺陷的生成对电子电导率的调制、对锂离子输运的影响、缺陷结构的可视化及缺陷进一步演化导致缺陷簇和超结构等。p在锂电池研究的材料中，除了常见的缺陷类型外，较为常见的缺陷还包括同一晶体结构中不同原子的互占位（antisite）、非整比（nonstoichiometry）、至少两种以上原子无序占据相同位置的固溶体（solid solution）、晶界（grain boundaries）、有序与无序共存的纳米结构（nanostructure）、包括微孔、介孔、大孔的孔结构（porous structure）、异质结（heterogeneous junction）、表面修饰层（surface coating layer）、梯度结构（gradient materials）、核壳结构（core-shell）等。如果同一个晶体结构同一个位置同一种原子存在两种以上的价态，还可能存在电荷无序或电荷有序的结构。由于锂电池一般工作在室温附近，目前还没有讨论材料中的自旋有序或无序结构，但确实有限过渡金属的电极材料由于多种价态原子的共存，可能存在着分布不均的磁畴，这方面的研究在锂电池领域还较少涉及。

电池材料中存在着哪些缺陷，以哪一类缺陷为主及一定温度下缺陷的浓度属于热力学问题，与材料的组成、晶体结构、制备过程有关。材料中缺陷的存在会显著影响电子与离子在固体内部、界面、表面的输运、储存与反应性质。离子的电导率与可参与输运的自由离子的浓度和离子的迁移率有关。离子在固体中的输运一般需要通过空位、间隙位、晶界、表面等介质和通道进行传输。1.电极材料中同一缺陷的存在，对于离子传导和电子传导的推动作用既有可能相同，也有可能相反。

缺陷结构的存在还有可能提供额外的锂的存储位置。锂在缺陷位置的存储可以是可逆的，也可以是不可逆的。例如锂在空腔中的欠电位沉积，在界面处的界面储锂，在表面的表面电容，均为可逆的储锂机制。材料表面的某些悬挂键、表面的新相，有可能引起不可逆的储锂。

含有缺陷结构的实际材料与理想结构的体材料相比，由于缺陷的存在，材料的生成能发生了变化，会影响材料的稳定性和反应性。

理解了材料的缺陷化学，通过可控的增加或减少材料中的缺陷，可以有目的的调控材料的输运、存储、稳定性和反应性。对材料中缺陷结构的控制、确认、分析以及建立起与之相应的准确、全面的物理、化学、电化学储锂特性之间的构效关系，是锂电池材料研究中的核心基础科学问题，也是实现材料理性设计（rational design）的关键。

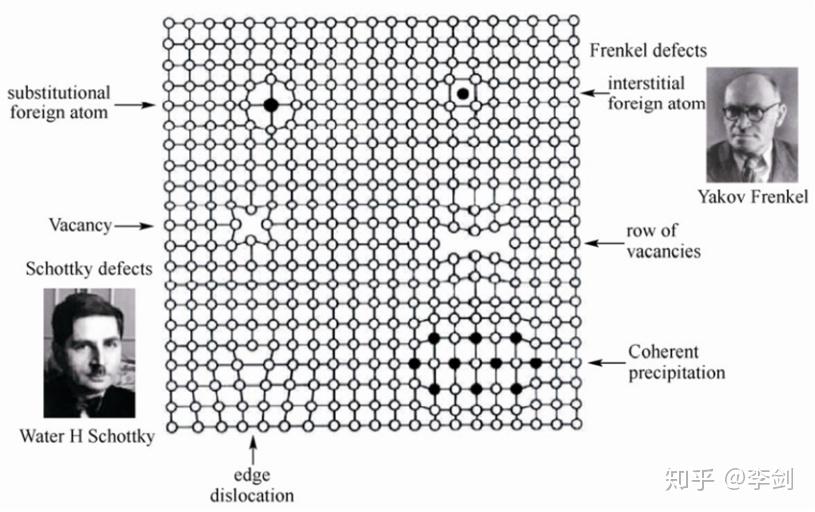
图23 固体中典型缺陷的原子结构示意图

材料中的缺陷和杂质会改变材料的许多性质，包括电子电导、离子电导等与锂电池性能紧密相关的性质。Hoang等通过第一性原理计算研究了橄榄石结构的LiFePO4中的本征缺陷及掺杂对其电子传导和离子传导的影响。计算结果表明，在LiFePO4中本征的锂空位缺陷和空穴小极化子分别决定着材料的离子输运和电子输运过程。对一价掺杂元素（Na、K、Cu、Ag），二价掺杂元素（Mg、Zn），三价掺杂元素（Al）、四价掺杂元素（Zr、C、Si）和五价掺杂元素（V、Nb），Hoang等分别计算了各种元素掺入不同晶格位置的缺陷生成能，不同合成条件对掺杂浓度的调节以及掺杂后体系输运性质的改变，发现通过缺陷控制的合成手段可能有效地改善体系的电子导电性。

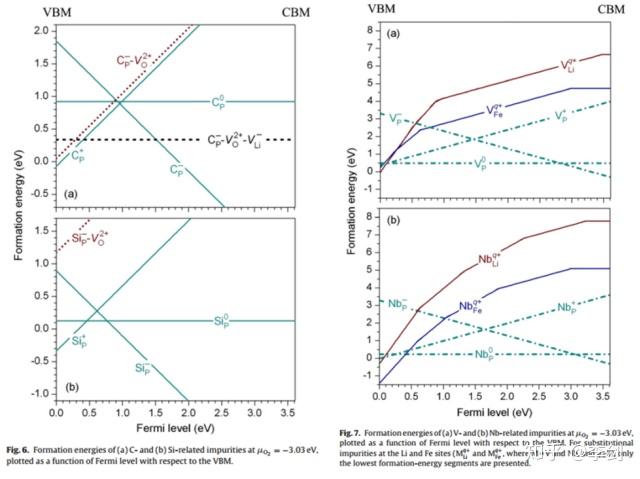
图24 缺陷形成能

2.1.7. 晶体结构及演化

电极材料在脱嵌锂的过程中，有时会出现一些有趣的结构演化过程，如在石墨嵌锂过程中出现的“阶”结构。近年来，随着透射电镜技术的发展，人们在LiFePO4的脱锂样品中观察到了三相界面，并且也发现了“阶”的现象。借助原子尺度的计算模拟，该结构的演变过程及形成机制得到了进一步的阐释。

Sun等通过第一性原理计算研究了LiFePO4脱锂过程中出现的“阶”结构（如图25）。结果显示，“阶”结构是一种受Li+传输动力学控制的热力学亚稳态。其成因在于，当一层脱锂出后其最近邻锂层的Li+跃迁收到阻碍，因此充放电过程中倾向于隔层脱锂而不是顺序脱锂。结合热力学条件，Sun等构建了一个用来描述LiFePO4充放电过程的双界面脱锂模型：充电时，LiFePO4颗粒同时存在两个隔层脱锂过程，它们在空间上有一定的相位差；经历过两个隔层脱锂过程的区域为“阶”结构，而两个隔层脱锂过程都没有经历过的区域为LiFePO4相。脱锂过程中“阶”结构位于LiFePO4与FePO4两相之间，该理论模型很好地解释了高分辨率扫描透射电镜下观察到的表象。

“阶”结构的形成表明，LiFePO4中Li+的占据与否会影响其最近邻锂层的Li+传输。由于LiFePO4是一个强关联电子体系，Fe 3d轨道电子高度局域，Li+占据/缺失带来的电子/空穴会局域在最近邻的铁离子上。因此，Li+可以通过改变其最近邻铁离子的价态来影响近邻锂层中的Li+传输行为。实际上是一种以铁离子为媒介的层间Li+间接相互作用。

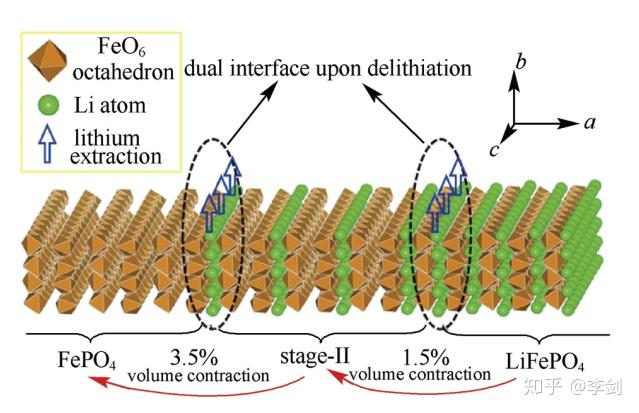
图25 LiFePO4充放电过程中形成的“阶”结构模型

2.1.8. 材料力学性能

大多数电极材料在反复的脱嵌锂过程中会经历体积的变化，如层状材料在脱锂后会出现沿c轴方向的体积膨胀，Si负极在嵌锂之后则会出现多达300%的体积膨胀。这就需要我们对材料的力学性能进行进一步研究，以理解材料在脱锂过程中形变产生的原因及对电池性能的影响。基于密度泛函理论的第一性原理能够通过求解力矩阵，获得材料的弹性常数，从而得到体模量、剪切模量、杨氏模量、泊松比等一系列力学性能的数值。

Shenoy等计算了不同Li含量的Li-Si合金的力学性质，建立了Si负极嵌锂过程中形变与断裂过程的力学模型，通过计算晶态与非晶态Li-Si合金相的杨氏模量、剪切模量、体模量和泊松比（图26），他们发现随着Li浓度的增加，上述模量值几乎呈线性降低，表明嵌锂引起了材料的弹性软化，同时也说明了材料的力学特性也在电池的电化学过程中不是保持不变的，应力场的分布与形变及裂纹的扩展都与放电状态相关。

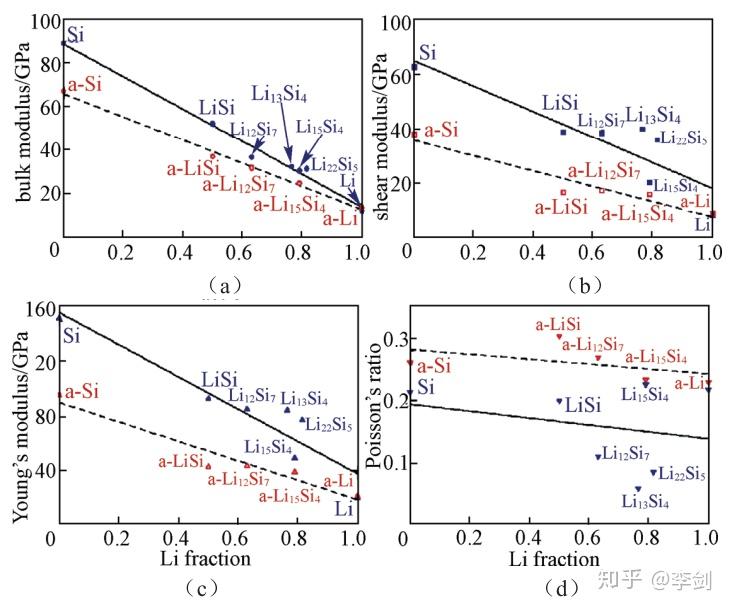
图26 计算得到的晶态（蓝色点）与非晶态（红色点）Li-Si合金LixSi在不同Li含量时的（a）体模量；（b）剪切模量；（c）杨氏模量；（d）泊松比

2.1.9. 离/分子吸附动力学模拟

在电池材料的DFT计算中，常出现离子/分子吸附能的计算，通过比较不同浓度下电极材料对金属离子的吸附可以估计电极材料对金属离子的储纳能力，进而估算电极材料的理论容量。锂硫电池是很有前景的高容量二次电池，很多锂硫电池材料的开发都致力于解决锂硫电池反应中间产物多硫化锂的溶解和穿梭问题。最近几年，DFT计算被很多锂硫电池的研究人员用来分析硫正极的基体或电池隔膜对多硫化锂的吸附能力。

吸附能可以通过DFT计算，Cui等人比较了一系列不同的含S的2D材料的化合物的吸附能。在电池材料的电化学反应中，离子的吸附对电极材料的反应性起关键作用，因此吸附动力学对电池的容量和循环性能有很大影响。 LSB的大量研究工作致力于解决所谓的“穿梭效应”。 一种有效且流行的方法是采用可以紧密固定可溶性多硫化物的硫主体。原则上，可以使用DFT计算吸附能，并且可以使用这些计算来量化设计的电池材料的性能。为了解决“穿梭效应”问题，Cui的研究小组比较了一系列二维潜在硫主体的吸附能，包括氧化物，硫化物和氯化物（图27），以及多硫化物在不同锂化条件下的吸附能。计算状态以获得锚固效应的趋势。如图27a所示，在锂化过程中，除了ZnCl2外，多硫化物与所有测试的2D材料的结合强度均会大致提高。通过比较，已表明V2O5和MoO3对多硫化物的锚固作用最强，这些DFT结果可为寻找有效的硫基质材料提供良好的指导。此外，在其DFT计算中分析了几种锚固材料的范德华（vdW）相互作用的贡献，他们发现随着锂化的进行，物理吸附逐渐转变成化学键与多硫化物的键合。该观察结果表明，在测量多硫化物和2D锚固材料之间的相互作用时，应将vdW校正包括在DFT计算中。

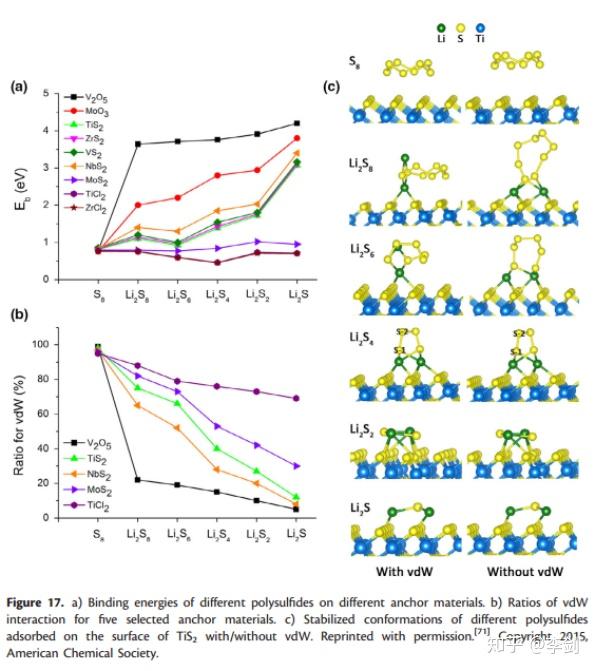
图27 结合能与vdW相互作用等

LiB电极表面上锂离子的吸附部分有助于锂离子的存储。尖晶石ZnFe2O4作为具有高理论容量的阳极，在初始放电过程中显示出高压平台。然而，这种平稳的行为不能用一般的锂离子嵌入来解释，直到郭等人，这种现象的原因仍不清楚。报告了他们的DFT机理研究。在他们的计算中，采用DFT + U方法计算了Li离子在ZnFe2O4不同表面上的吸附能（图28）。计算了不同浓度的锂离子在不同吸附位点上锂离子的结合能，从而发现了最活跃的吸附位点和锂的储存容量。与ZnFeO2端接的（110）表面相比，O和Zn端接（111）的表面与Li离子的相互作用更强，并且当更多Li离子吸附在表面时，结合能增加。这些结果证明了Li在ZnFe2O4（111）表面上的有效存储。此外，计算和实验证实，最初的高放电电位源自锂离子在以Zn为末端的ZnFe2O4（111）表面上的吸附。

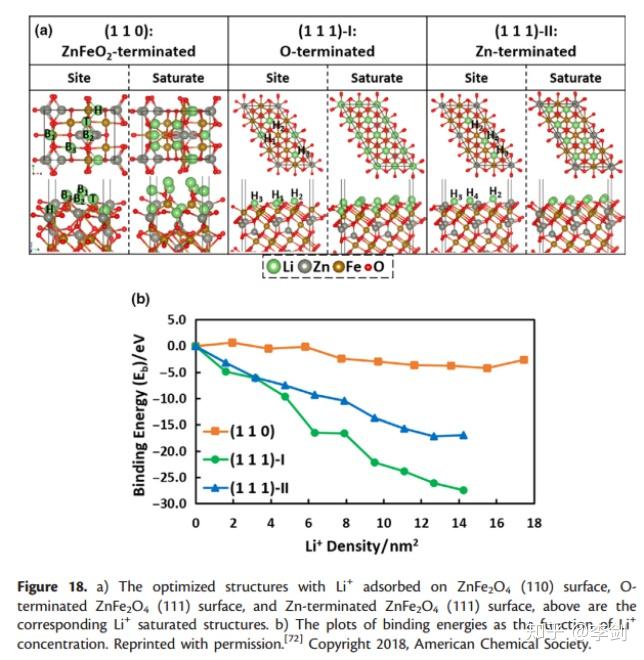
图28 （a）优化结构；（b）不同锂离子浓度与结合能关系

用于LIB的硅基负极材料具有较高的比容量，但其实际应用存在两个主要障碍：1）充电/放电过程中Si的体积变化大； 2）电导率低。已经表明将Si负载到N掺杂的石墨烯（NG）上可以有效地改善电导率并减轻体积改变效果。另外，NG会增加Li的吸附量，这已由Zou等证实。在最近的DFT研究中。他们发现，Si2，Si3和Si6团簇与NG具有很强的结合力，而Si6团簇具有最短的Si-C键长。活性最高的吸附位是被N原子包围的C原子。计算了Li在不同数量的Li原子的不同Si6 / NG杂化结构上的吸附能（图29）。尽管吡咯N均显示出对Li离子的强吸附能力，但其对Li离子的吸附作用却比吡啶N更好。此外，无论在吡啶二价N-或吡咯N-掺杂的石墨烯上，单个Li的吸附能都比四个Li的吸附能高。相比之下，吡啶吡啶N掺杂石墨烯是吸附多个Li离子的最有效部位。

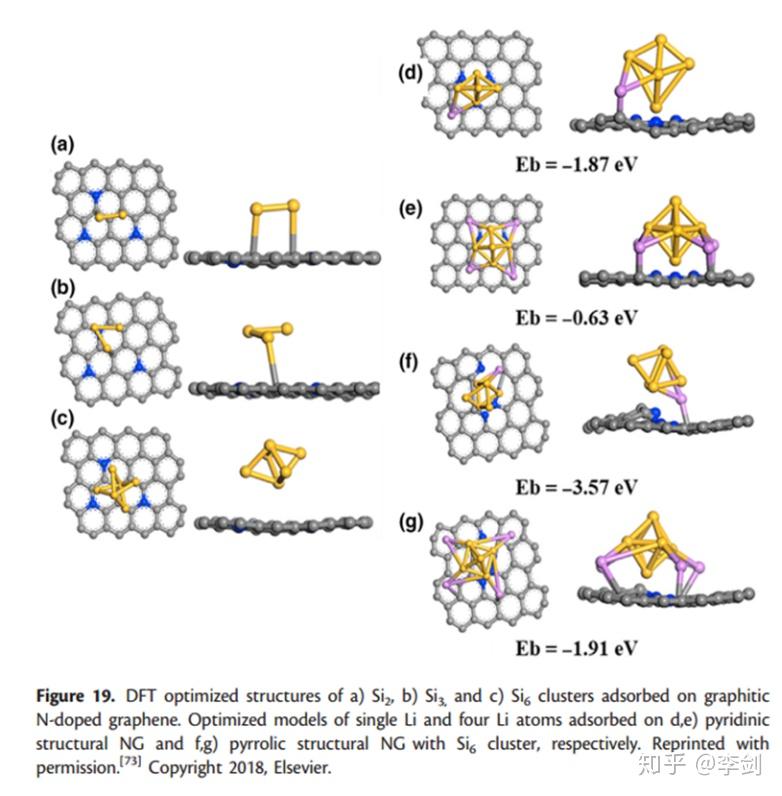
图29 结构优化

总体来说，DFT不仅可以支撑实验，也可以预测和虚拟筛选新型电池材料。

2.2. 量子化学方法

近年来随着高性能计算机的出现，量子化学计算方法的应用也越来越广泛，使其研究对象不仅是过去的小分子而且对较大的、电子离域性更强的分子研究成为可能，这奠定了量子化学计算方法在锂离子电池电解液研究中应用的基础。量子化学方法具有其它研究方法如电化学方法、在线谱学分析方法等所不具备的优势，它可以很清楚地给出化学键的形成和断裂过程的电子因素，提供反应详尽的热力学和动力学参数，给出每一步反应中过渡态的信息，从而可以全面掌控整个反应的发生。

量子化学方法在锂离子电池电解液研究中的应用主要有以下几个方面：新型锂盐的设计和电化学性能验证，功能组份的作用机理，电极 /电解液界面膜的形成机理和成份分析，以及溶剂和添加剂在成膜过程中出现的过渡态的情况等。目前得到应用的计算方法主要有：Hartree-Fock( HF)、密度泛函理论(DFT)以及 MP2 等。主要研究的量子化学参数有：最高占据轨道(HOMO)能量、最低空轨道(LUMO)能量、偶极矩、电荷布居分布以及反应过程的热力学势等。

2.2.1. 量子化学计算在新型锂盐设计上的应用

发展新型的锂盐，重点在于找到最合适的阴离子与 Li+配合，阴阳离子之间的相互作用决定了锂盐的溶解性、离子电导率、电化学窗口和热稳定性等，通过量子化学指导下的计算机模拟能够很好地弄清锂盐结构与性能的关系，节省了实验研究的时间。通过对锂盐的电子结构、能量和轨道进行计算研究，可以在量子化学水平上加深对锂盐的认识。

前线轨道(LUMO、HOMO)能量的高低在很大程度上反映了分子的物理化学性质。根据 Klopman理论，阴离子的硬度由 HOMO 能量决定。根据软硬酸碱理论，硬酸倾向与硬碱结合，而 Li+为硬酸，所以如果与 HOMO 能量高的阴离子结合该锂盐就有较好的热稳定性。通过密度泛函理论计算了 LiBCB，LiSCB，LiBSB 锂盐的结构和阴阳离子之间关系，能量计算得到这 3 种物质四面体结构为最稳定结构。轨道分析发现，在分子中存在金属螯合氧原子和反键轨道阳离子之间强烈的离域相互作用。对 3 种阴离子进行计算得到，BSB－具有最高的 HOMO 能量，所以 LiBSB 具有最强的电荷离域现象和较强的酸性，因而具有较好的热稳定性。

Barthel 等采用半经验分子轨道理论证明了烷基硼酸锂盐的氧化分解电位与 HOMO 能量之间存在线性关系。Xu 等对 LiBOB 系列的锂盐在溶剂碳酸丙烯酯( PC) 中的氧化分解电压计算发现，其与HOMO 能量都存在很好的线性关系。锂盐为极性分子，当其在极性溶剂中溶解时，其溶解度与偶极距有直接关系。锂盐的偶极距越大，其溶解度也越大。对于结构相似的锂盐而言，其离子电导率主要取决于离子的解离程度，所以锂盐结合能的大小可以反应锂盐溶液的电导率趋势。

Kita等对不同阴离子的锂盐 LiPF6 -n(CF)n的计算得到了不同阴离子锂盐的电导率和氧化电势，结果表明，阴离子的热稳定性具有如下的顺序:PF4( CF3)－2> PF3( CF3)－3> PF5( CF3)－> PF－6。锂盐的解离能力顺序为:LiPF3( CF3)3> LiPF4( CF3)2> LiPF5( CF3) > LiPF6。在 0. 1mol/L(锂盐 /PC∶ 1，2-二甲氧基乙烷( DME)) 电解液中的导电率 LiPF4( CF3)2略低于 LiPF6(4. 4mS /cm)。在 PC 中的氧化电位LiPF4(CF3)2较 LiPF6高。同时，用 LiPF4(CF3)2作为电解质的电池比用 LiPF6作为电解质的电池显示出较好的循环性能。相关锂盐阴离子的 HOMO 能量值列于表2 中。

表 2 不同锂盐阴离子的 HOMO 能量值

2.2.2. 量子化学方法在功能添加剂设计上的应用

2.2.2.1. 量子化学计算在电解液锂盐添加剂研究中的应用

2.2.2.1.1. 电解液锂盐添加剂电化学性质

电极 / 电解液界面膜(SEI 膜)是电解液成分分解产物富集于电极材料表面而形成的一层致密膜状结构，其允许锂离子通过的同时可以有效阻止电解液与负极进一步接触反应，成膜添加剂应具有高的还原电位和低的氧化电位以便优先于电解液中其他组分被氧化还原，还应具有 Li+ 与添加剂分子之间的相互作用力比其他分子更弱的特点。

根据文献提出的前线轨道理论，分子得失电子主要发生在其最低非占有轨道(LUMO)和最高占有轨道(HOMO)，LUMO 能级与 HOMO 能级的高低分别反映了分子的耐氧化 /

还原性质。一般认为，锂盐添加剂的 LUMO 能级应低于溶剂或HOMO 能级应高于溶剂，即可以被优先还原 / 氧化形成 SEI膜。在量子化学计算过程中，人们通常使用极化连续介质模型(PCM)来更精确地描述锂盐添加剂在溶剂环境中的物化性质。

对几种硼酸盐的分子模型研究表明，在电解液体系中硼酸盐的 LUMO 能级显著低于常用碳酸盐电解液，即具有优先还原成膜的作用。Ramaite 等研究发现了一种类似于硼酸盐的添加剂锂 -12- 冠 -4 配合物，通过计算该添加剂前线轨道能级，发现该添加剂可优先于电解液其他组分在负极表面还原生成 SEI 膜，有效抑制溶剂的分解。同时，计算了常见碳酸盐和苯基硼酸衍生物的 HOMO-LUMO 能级间隙，对比可知，碳酸盐 HOMO-LUMO 能级间隙普遍大于苯基硼酸衍生物，则说明碳酸盐的电化学稳定性高于苯基硼酸衍生物。这说明从氧化还原电位方面考虑，苯基硼酸衍生物可以作为电解液锂盐添加剂。

2.2.2.1.2. 电解液锂盐添加剂在电解液中反应机理

研究者可通过优化锂盐的几何构型得到过渡态能量，进而得到锂盐的最优还原反应路径，为研究锂盐添加剂的成膜机理提供理论依据。Li 等通过量子化学计算探索了添加剂LiBF2SO4 的还原机理及可能的还原路径。通过计算还原路径的反应势垒发现，在还原分解初始阶段，LiBF2SO4 得到一个电子形成阴离子基团 [LiBF2SO4]－，[LiBF2SO4]－有两种分解路径，路径1的势垒(9.57 eV)低于路径 2(13.06 eV)，故[LiBF2SO4]－的还原路径为路径 1，[LiBF2SO4]－和两个 Li+ 结合经过过渡态生成SO2、LiF 和 LiBO2·LiF。由此可得，在首次放电过程中，SEI 膜组分中含有大量的含硫化合物与硼酸盐化合物，含硫化合物有利于锂离子的迁移，能减小阻抗，形成良好的 SEI 膜 。

2.2.2.1.3. 电解液锂盐添加剂的结构优化及虚拟筛选

目前在文献中报道的添加剂已不能完全满足人们对于锂盐添加剂性能的要求，研究者需寻找新型锂盐添加剂来进一步提高电池性能。基于量子化学的虚拟筛选技术是目前成本较低，自动化程度较高的方法之一。研究者可通过指定量子化学参数来判断该物质的物理化学性质，以此从特定物质群中筛选出具有指定性质的个体。三 (三甲基甲硅烷基) 硼酸盐 (TMSB) 是一种用于改善LiPF6 基电解质循环性能的电解液锂盐添加剂。Han 等通过分析该锂盐构效关系，认为该物质可以与 PF6－(或 F－)结合，能促进 LiPF6 解离，还会分散 PF6－的电子，提高 LiPF6 盐的热稳定性。根据该机理，通过寻找具有更高 F－结合亲和力且具有更低 HOMO 能级的物质来进一步优化电解液性能。通过筛选，在 33 种用于负极成膜的硼酸类添加剂中优选出了五种性能优异的负极成膜添加剂。同时，指出这种筛选优异性能添加剂的方法适用于很多类似的添加剂，如亚磷酸盐和磷酸盐。综上所述，研究者可通过量子化学计算得到锂盐分子结构与物理、化学性质之间的关系，氧化还原过程路径以及结构变化规律，为研究锂盐添加剂的作用机理提供依据。同时，基于量子化学计算的虚拟设计和筛选，研究者可以从大量已报道甚至未发现的物质中得到满足性能要求的物质，极大地加快实验进程，对锂盐添加剂的研究具有重要的意义。

2.2.3. 量子化学计算在电解液溶剂添加剂研究中的应用

目前，量子化学计算在电解液溶剂添加剂中的应用主要包括：成膜添加剂的筛选、优化及成膜机理的探索；正极表面具有高氧化态的过渡金属离子与溶剂添加剂之间反应的研究；添加剂构效关系的研究。

Murdock 等根据电离势和电子亲和势分别与 HOMO 和LUMO 能量具有的近似线性关系，以化学硬度的观点表述添加剂的该性质，即成膜添加剂需要具有比其他电解液组分更低的化学硬度。

研究者们通常会通过比较键长的方法来判断该添加剂相对于其他组分与锂离子之间相互作用的强弱，同时也可通过自然布局(NBO)分析，极性较大的分子更有利于沉淀在电极表面形成固态膜结构。

Leggesse 等通过对比亚乙基亚硫酸盐(VES)在真空和溶剂化环境下两种单电子还原路径的反应势垒及吉布斯自由能发现，阴离子自由基2经过断裂 S-O 键形成过渡态3，通过C-O 键断键最终形成 SO2 自由基和 CH2=CHCH2CHO，以上还原产物会经过 进 一 步 反 应 生 成 碳 酸 锂 、Li2S2O4、Li2SO3 和Li2S2O5 等固态物质，组成 SEI 膜。除此以外，阴离子自由基离子 2 还可以与 Li 结合生成中间体 7。该中间体经过 C-O 键的断裂形成过渡态 8，进而生成中间体 9，中间体 9 自解离形成亚硫酸根阴离子(LiSO3－)和丁二烯的弱络合物，LiSO3－可以作为良好的亲核试剂与被 VES 溶剂化的 Li+ 反应生成(C2H3OSO2Li)2 或 CH2(OSO2Li)CH2OCO2L，从而组成 SEI 膜。

溶剂在正极表面的副反应主要是材料中高氧化态的过渡金属离子引起的，若该金属离子可以优先与电解液溶剂添加剂发生反应，则会使之氧化性减弱，减少正极材料表面电解液的分解，改善锂离子电池的性能。己二腈(ADN)能够有效改善电解液的耐高压性能，Li等计算了碳酸酯溶剂中 ADN、DFOB－和 Ni4+ 的 HOMO 和LUMO 能级，并比较了 Ni4+ 离子与各组分 HOMO 能级之间的差值。结果表明 Ni4+ 的 LUMO 能级与 ADN 的 HOMO 能级之间的差值最小，即 Ni4+ 将会优先与 ADN 结合。其次，通过对比ADN 得电子前后的分子结构(图 1)，认为 ADN 中 C2 和 C3 之间的共价键有断键的趋势，进一步证明了 Ni4+ 与 ADN 分子之间存在自发化学反应的猜想。根据以上结论得到电极反应式，如式(2)所示：

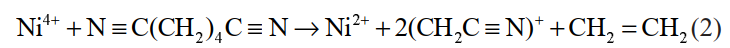
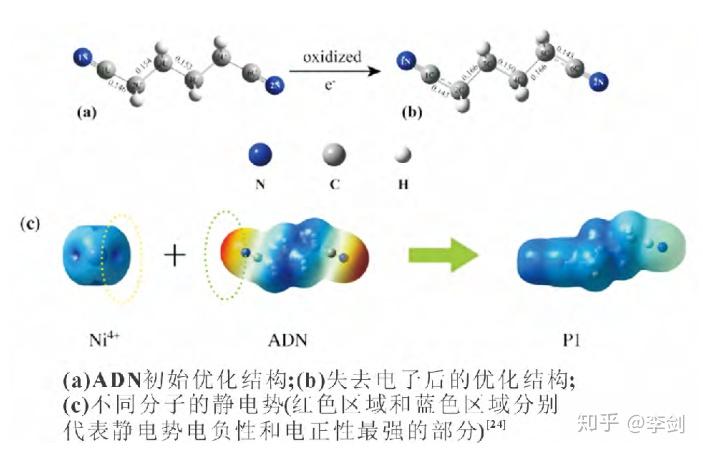
图30 ADN 初始优化结构和失去电子后的优化结构的比较及不同分子的静电势

这种通过研究正极材料中过渡金属离子与电解液添加剂的相互作用的方法突破了以往将电解液在电极表面反应独立考虑的限制，对今后添加剂机理研究有较强的指导意义。相较于锂盐，溶剂添加剂方面的虚拟合成和筛选更倾向于考察官能团类型与位置对物质性质的影响。Park等提出，苯环上取代的杂原子、异构体以及环状有机分子中双键的数目很大程度上影响其还原电位。研究环状有机分子的结构特征(如环个数、取代杂原子类型等)与其电子效应之间的关系，可以构造具有特定性能的添加剂。分别以原子和官能团的种类及数目为变量计算了原子和分子的氧化还原电位，通过对比发现：含有 N-H 官能团的化合物大多数适合用作负极的成膜添加剂；含有两个氮杂原子的萘的异构体适用于正极的成膜添加剂；单环、杂环的化合物或含有与环戊烷或苯环进行杂原子取代的化合物适用于正极的防过充添加剂。

综上所述，通过量子化学计算可以研究电解液溶剂添加剂在界面膜中的成膜机理，并根据构效关系进行进一步优化和筛选，在今后改善锂离子电池性能方面将起到重要作用。

采用量子化学的方法来研究添加剂的作用机理已经有较多的文献报道。对于锂离子电池有机电解液成膜功能分子而言，分子的 LUMO 能量越低，还原电位越高，越有利于在石墨负极表面形成固体电解质(SEI)膜。Xu等用密度泛函理论中的 B3LYP 方法，以 6-31 + G( dp) 为基组计算了溶剂分子碳酸乙烯酯(EC)、PC、碳酸甲乙酯(EMC)及成膜功能分子 1，3-丙磺酸内酯( PS) 和 1，4-丁磺酸内酯( BS) 的前线轨道能量，发现 PS、BS 具有比溶剂分子更低的 LUMO 能量。同时电化学实验表明 PS、BS 优先于溶剂分子在石墨电极表面还原分解形成稳定的 SEI 膜。

Wang等通过密度泛函方法计算了 EC 溶剂中的碳酸亚乙烯酯( VC) 在成膜过程中起到的作用。通过计算发现，在锂离子电池预充过程中，VC 得到电子形成稳定的过渡中间体，由于这种中间体想要进一步还原需要克服较高的能垒，所以得到电子后的中间体引发了溶剂 EC 的还原分解。与 EC 的还原产物比较，VC 的还原产物是一些含有双键的物质，这种双键产物会在电极表面发生聚合，达到改善 SEI膜性能的目的。Ken等通过采用 HF 理论计算了不同溶剂和添加剂在锂离子电池中所发生的还原反应，其中包括 EC、PC、VC、乙烯基碳酸乙烯酯(VEC)、四氢呋喃( THF) 和乙烯基碳酸亚乙烯酯( VVC) 等物质，通过计算势能面的鞍点能得到每一种溶剂和添加剂的过渡态、发生还原反应的产物和方程式，并计算了每种物质发生反应的活化能和反应能量，添加剂 VC 具有比 EC 和 PC 低的活化能，添加剂 VVC具有最低的反应活化能，这主要是由其共轭结构所导致的，所以 VVC 应该是一种性能优异的 SEI 膜成膜添加剂。

李丽等通过实验证明，添加剂 BS 能够使 PC 作为溶剂的电解液具有很好的电化学性能，也就是说，添加剂 BS 具有很好的成膜性能。接着进一步对 BS、PC 的总能量及前线分子轨道能量进行计算，结果表明 BS 的总能量和 LUMO 能级数值远远低于 PC，表明 BS 具有较强的得电子能力，更易于被还原。

Ken等对一系列氮醚添加剂对锂盐 LiPF6离解能力的影响进行了研究，通过计算得到，氮醚的尺寸和结构对 LiPF6离解有很大的影响，而且环状醚比线状醚具有对 LiPF6

更强的解离能力；并得到当含氮原子数为 8 时，锂盐的解离度最高。接着 Ken 等又通过计算确定了 12-冠醚-4 是在 LiPF6电解液中最好的导电添加剂，能够实现锂盐电解质阴、阳离子对的有效分离。

量子化学计算已经在锂离子电池电解液添加剂研究中广泛应用，研究者可以通过量子化学计算方法，对比电解液各组分的 HOMO、LUMO 能级，从而得知物质的氧化还原顺序。在进一步的研究中，研究者可结合显微、波谱、色谱等分析测试手段的表征结果，通过量子化学计算，得到化学反应路径，从而在分子尺度上了解添加剂的作用机理。同时，量子化学计算所具有的高并行性和系统性决定了该方法可以通过一定的程序实现高自动化、高通量的工作，从而为研究者提供了一种优化电解液性能的简单方法。值得注意的是，由于目前量子化学计算的自身限制，该方法还不能完全代替实验，但是随着人类对自然科学认识的不断深入，利用具有更强计算能力的计算机，结合更精确的计算方法，量子化学计算必将在锂离子电池电解液添加剂领域中有更为广泛的应用。

2.2.4. 量子化学方法在电极 / 电解液界面膜研究中的应用

通过量子化学计算方法来研究电极 /电解液界面膜的形成具有常规检测方法无法比拟的优势，通过理论计算能够判断到底是哪种物质参与了界面膜的形成，在成膜过程中决定键的形成和断裂的电子影响因素以及在成膜过程中的热力学和动力学过程分析等。通过实验方法已经建立了 4 种模型用于解释锂离子电池负极碳的界面情况，虽然目前引用率最高的是 SEI 模型，但是这些模型都存在一些争议，随着量子化学方法的发展，采用理论计算的方法研究界面膜已经成为研究热点。

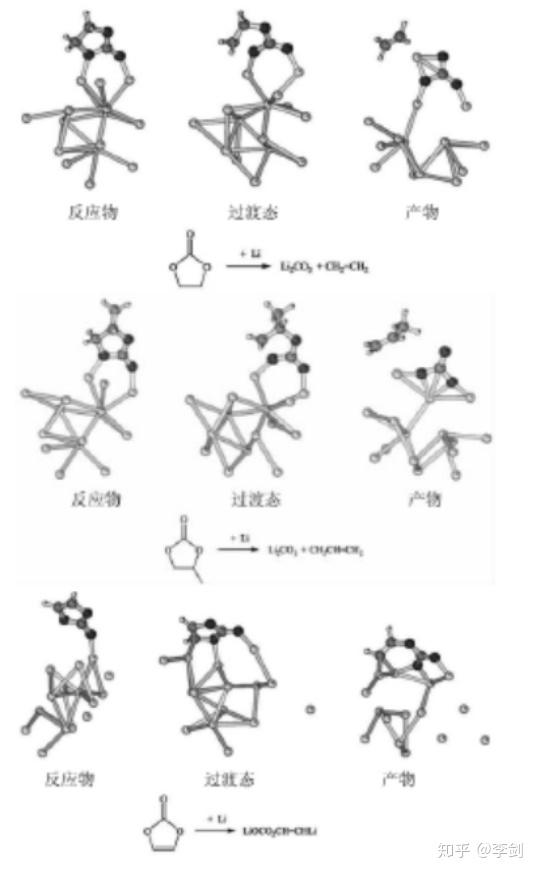
图 31 溶剂 EC，PC 和添加剂 VC 的成膜反应式

Ken等进行了锂盐在溶剂 EC、PC、γ-丁内酯、碳酸二甲酯( DMC)、EMC 和碳酸二乙酯( DEC) 以及它们的混合溶剂中 SEI 膜形成的热力学分析。通过计算得到，在液相中，环状溶剂和链状溶剂得到第一个和第二个电子被还原都是发生放热反应，一般情况下，环状碳酸酯比链状碳酸酯更容易被还原，环状碳酸酯中 VC 是最容易得到 2 个电子被还原的，所以它被认为是比较有效的一种 SEI 膜添加剂。同时通过对溶剂 EC 和 PC 进行计算发现，EC 基电解液能够快速形成致密且不溶于电解液的 SEI 膜，而PC 基电解液则恰恰相反。图 31 为通过计算得到的溶剂 EC、PC 和添加剂 VC 发生还原反应的产物。

2.2.5. 小结

综上所述，量子化学原理在锂离子电池电解液的研究中有着广泛的应用空间。通过量子化学理论计算得到的溶剂或者添加剂的理论还原电位与实验事实能够较好地符合，可以用来行有效地指导新型功能添加剂的开发和使用;也可用量子化学原理从理论上解释新型电解质锂盐的相关特性，为合成和设计新型锂盐提供了大量理论参数。值得注意的是，量子化学计算不能取代实验工作，但它能够对一些功能组分进行预测，对锂离子电池电解液整个体系进行系统优化，对实验结果进行解释，能够避免盲目的实验工作。随着人们对化学物质的进一步认识和计算机水平的发展，相信量子化学原理在锂离子电池电解液研究领域中的应用会更广泛和深入。

2.3. 平衡态密度泛函理论与非平衡态密度泛函理论（NEGF-DFT）

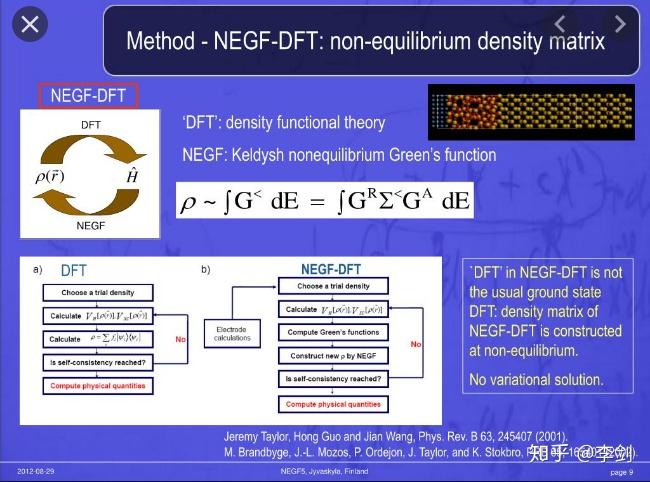
图32 NEGF-DFT

以周期性材料体系计算的密度泛函理论常用于材料设计等领域，而孤立体系的计算一般亦可采用量子化学方法等第一性原理方法进行计算。由于外加电场的作用导致原来的材料在电场作用下变为了非平衡态体系，因此常规的平衡态方法只能用于计算平衡态下的电子电导而不能去进行非平衡态的电子输运计算。非平衡态电子输运有多种方法计算，其中精确度最高，从第一性原理出发的方法为NEGF-DFT，非平衡格林函数-密度泛函理论。

2.3.1. 硅材料表面电学性质研究

硅材料表面由于原子厚度的台阶层的存在，导致在采用量测设备进行测量时会因为测量一致性的问题导致数个数量级的误差。Guo等人猜测是因为表面台阶层的存在，采用实验与计算结合的方式，进行验证和计算。采用NEGF-DFT方法构建不同级别原子台阶，计算其电子透射率，发现原子台阶层的存在会导致材料电学性质出现数个数量级的波动。

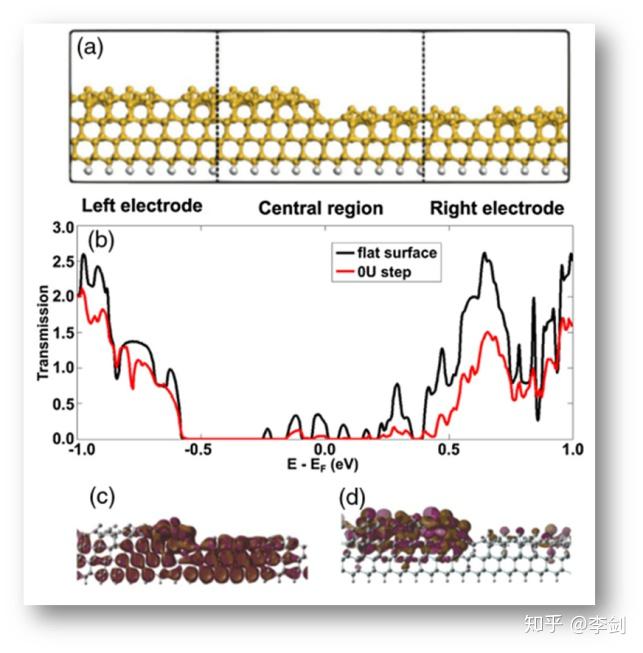
图33 基于NEGF-DFT计算硅材料表面电学性质

2.3.2. 石墨烯电容器电子输运研究

超级电容器的一个巨大挑战是同时实现高能量容量和快速充电/放电率。具有大表面积的多孔石墨烯是一种很有前途的超级电容器电极材料候选材料。赵纪军等人利用第一性原理计算和非平衡格林函数，探讨了不同空穴缺陷和/或氮掺杂的石墨烯片的形成能、力学性能、扩散行为和电导率。有趣的是，与吡啶象孔石墨烯（尤其是六边形孔）可以更容易地氮掺杂而且仍然保留了原始石墨烯的优良的机械性能，有利于循环使用寿命长。孔直径为4.2−10Å的多孔石墨烯电极有助于得到高效的电解质和优异的倍率性能。此外，掺杂氮作为电子供体或质子吸引子导致电荷积累和产生更高的赝电容。氮掺杂石墨烯的透射系数对纯净的石墨烯只有中等程度的降低和对详细的几何参数不敏感。

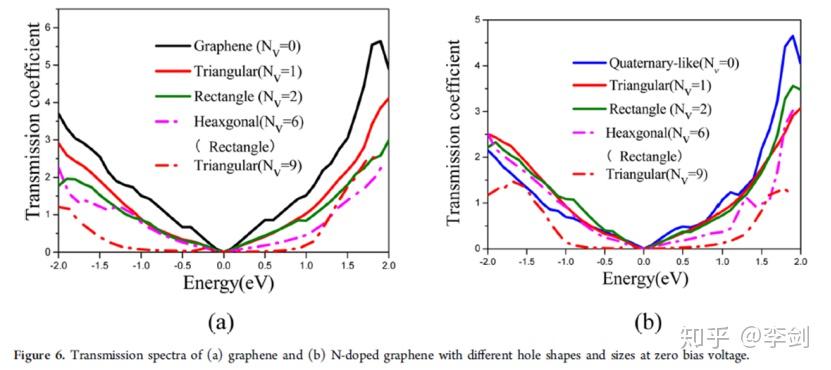
图34 基于NEGF-DFT方法进行石墨烯材料电子输运性能研究

2.4. 第一性原理评价与瓶颈

电池材料计算常采用的泛函方法，包括半局域泛函（LDA，GGA，meta-GGA，GGA+U）、杂化泛函（HSE06）。半局域的密度泛函方法，不能很好的处理电子的相关交换能，在计算体系中出现电子转移的时候，往往会有不可忽略的误差。Cococcioni et al发现LDA和GGA得出的锂离子嵌锂电位往往比实际电位低零点几电子伏特。金属Li中非局域电子的自相互作用很小，而过渡金属的d轨道电子的自相互作用很大，当金属Li中的非局域电子转移到过渡金属d轨道，实际上能量变化比较大，而LDA和GGA会低估能量变化，从而低估反应电势。GGA+U是一个半经验的方法，U值需要通过实验值来进行校正。同一种元素在不同化学环境下，可能需要采用不同的U值。因为这种方法，U值的确定是十分关键的。HSE06是通过引入一定比例的Hartree-Fock交换能来降低电子自相互作用能的误差，计算精度较高，但计算量比GGA和GGA+U大很多，需要大量的计算资源。Chakraborty et al (npj Comput. Mater. 2018, 4, 60.)基于对过渡金属氧化物正极储锂性能相关的计算，总结出，meta-GGA泛函SCAN，能很好的描述中程范德华作用，在分析电子结构和晶胞参数、预测结构稳定性上比其他的半局域泛函更好。在某些情况下，SCAN的准确度可以与HSE06匹敌。对于电池材料能量相关的计算，SCAN一般比LDA和GGA更好。但是对于弱束缚体系，如合金，SCAN比GGA的计算误差更大。在实际计算当中，需要根据材料体系、计算资源和计算内容选择合适的密度泛函方法。

2.5. 破局与展望

第一性原理在锂离子电池材料研究中得到了广泛应用，然而存在计算体系较小，常规方法采用的方法对于适用性以及计算精度仍有问题，因此需要在确保精确性和准确性的基础下，开发大尺度DFT计算软件。

3. 分子动力学

基于密度泛函的第一性原理能够得到材料出于零温状态时的性质，这对理解材料的本征特性非常重要。在有限温度下材料中原子、离子的输运可通过分子动力学模拟进行研究。本节将介绍分子动力学方法及其在锂离子电池中的应用。

分子动力学是一门结合物理，数学和化学的综合技术。分子动力学是一套分子模拟方法，该方法主要是依靠牛顿力学来模拟分子体系的运动，以在由分子体系的不同状态构成的系统中抽取样本，从而计算体系的构型积分，并以构型积分的结果为基础进一步计算体系的热力学量和其他宏观性质。

分子动力学模拟是研究微观世界的有效手段"其势函数和数值算法对模拟的精度有较大影响，为了提高势函数的精确性，将基于局部密度泛涵理论的从头计算分子动力学， 量子化学分析参数拟合和蒙特卡洛方法相结合有望成为研究势函数的最佳方法，随着计算机性能的不断提高，摆脱了经验势函数的从头计算分子动力学的应用范围将会不断扩大，计算的精度也会不断提高。所以，从头计算分子动力学将会成为分子动力学模拟未来的主要发展方向。

分子动力学中按照力的计算方法不同可以分为经验势方法（MD/MM等）、半经验势方法（TBMD等）和第一性原理分子动力学（FPMD）。

3.1. 分子动力学模拟所获得信息

分子动力学模拟可以获得包括原子的位置和运动速度等原子尺度的信息。统计力学能把这些原子尺度的信息转换为宏观可观测量，如能量、比热容、压强等。这样的转换基于各态历经假设（ergodic hypothesis），即统计系统平均等效于对时间的平均。最基本的思想是：分子动力学的目的是通过模拟系统在足够长的时间里系统随时间的演化过程，从而产生足够多的满足我们需要的相空间的各种构型，然后对这些构型进行平均，得到诸如结构、动力学、热力学等宏观性质。在锂锂电池中我们主要希望获得材料中离子的扩散系数和迁移路径。

虽然分子动力学可以模拟系统粒子随时间的演化，查看离子迁移的路径，计算粒子的扩散系数以及材料的稳定性，但是粒子运动的规律是牛顿力学，对质量较轻的粒子比如氢气和氦低温存在量子效应计算效果不理想。

3.2. 分子动力学在锂电池中的应用

分子动力学不仅可以揭示材料中离子自扩散过程中的运动路径、能量势垒，也为我们理解材料中离子的扩散机制提供了可能。Yang等通过计算LiFeO4的自扩散过程，发现该材料中的Li+的迁移并不是连续发生的，而是如图所示通过相邻晶格位置之间逐渐推进的跃迁发生的。Yang等的模拟不仅发现了Li+沿着一维方向的“之字形”路径前进的过程，还发现了Li-Fe离子的协同运动，这种协同运动导致了Li/Fe互占位且有利于Li+在通道之间的扩散。

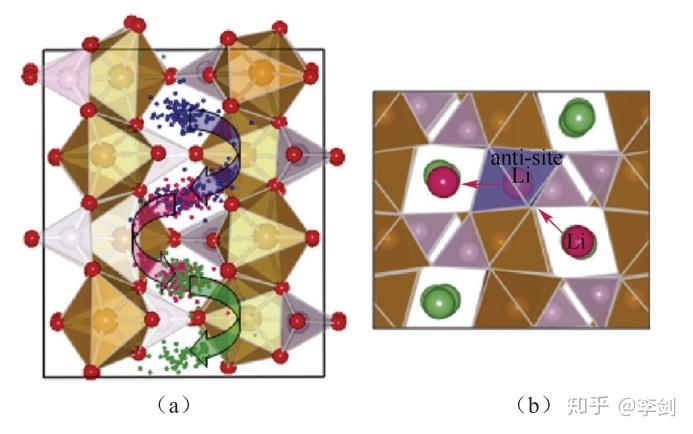
图35 模拟得到Li离子在LiFePO4中的运动轨迹（a）及锂离子通过Li/Fe互占位缺陷在通道之间的迁移（b）

3.3. SEI膜建模计算与设计

电池中固液界面的性质对锂离子电池充放电效率、能量效率、能量密度、功率密度、循环性、服役寿命、安全性、自放电等特性具有重要的影响。对界面问题的研究是锂离子电池基础研究的核心。

固体电解质膜(SEI)是影响有机液态锂离子电池稳定性、倍率性能和循环寿命的关键因素，由于其复杂的成分结构及动态的固液界面，仅从实验上难以清晰地给出其结构成分特征、离子/电子传导特性、化学/电化学稳定性等物理图像，急切需要结合理论模拟来全面深入理解上述性质，进而加速SEI膜的改性研究进程。

上海大学施思齐教授与密歇根州立大学Yue Qi教授以及中国科学院物理研究所李泓研究员在npj computational materials合作发表题为“Review on modeling of the anode solid electrolyte interphase (SEI) for lithium-ion batteries”的专题综述文章，文章概括了近年来利用多尺度计算模拟方法对锂离子电池负极SEI膜的理解、预测与设计，详细综述了SEI的形成过程、形成原理及改性方法。

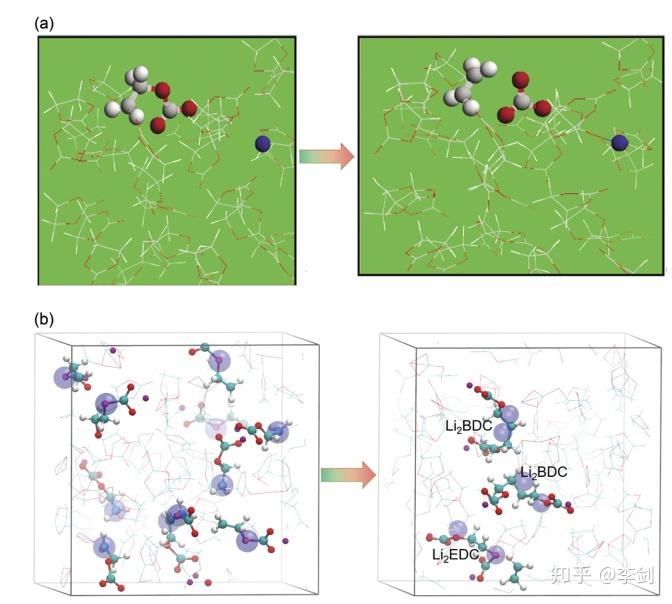
图36 介绍了第一性原理分子动力学(AIMD)及经典分子动力学(eReaxFF反应力场)预测EC还原反应路径的比较，能够准确描述电荷转移是经典MD反应力场模拟方法在时间尺度上的精细化。（a）改编自Yu的快照，分别是在0 fs和55 fs后向EC液体中添加了第二个多余的电子。 配色方案：C灰色，H白色，O红色，Li / Li +蓝色。 带有两个多余电子的EC表示为圆棒图，而其他所有完整EC则为棒图（版权：电化学学会）。 b带有过量电子的液态EC的快照。 配色方案：C青色，H白，O红，Li +紫色，电子大的蓝色球体69（版权所有：美国化学学会）

Takenaka等人开发了一种混合方法，该方法将MD（使用经典力场）与MC（由DFT计算的反应能）相结合，以克服SEI形成的时间和长度尺度。 在他们的模拟中观察到具有两层结构的纳米厚的SEI膜。 下图所示为定性合理的SEI形成图。但在当前模型中所有反应速率都设置为相等，从而限制了其预测能力。如果具有正确的反应速率，扩散速率，电子隧穿和传输速率以及电解质分子的重组能，可以将其扩展为多尺度SEI形成模型。

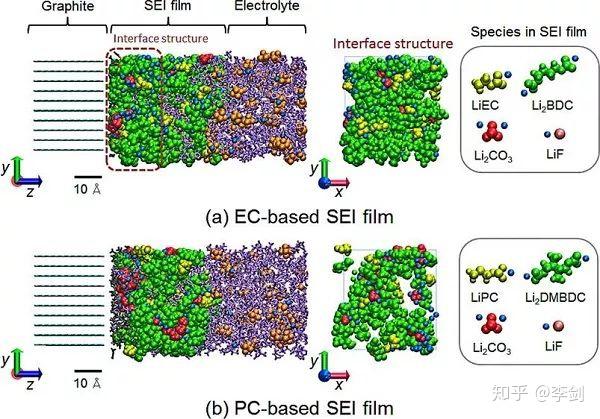
图39 结合经典分子动力学及蒙特卡洛方法给出了纳米尺度的SEI“表面生长”模型。SEI膜和电解质的快照。 配色方案：SEI胶片绿色，Li +蓝色，PF3（C2H4或C3H6）灰色，EC（PC）紫色，PF6-橙色。 左图为侧视图，而中图为右图，表示SEI膜中界面结构的正视图（从块状电解质侧面观察深度0≤z≤20Å可见）（版权： 美国化学会）

4. 键价和方法（BV）

4.1. 键价和方法简介（BV）

锂电池中核心的动力学过程是锂离子的输运，离子传输的快慢和路径直接影响电池充放电的性能。在固体和液体中，离子的传输是通过离子向近邻位置随机跳跃的扩散过程实现的。离子在运动过程中会受到由周围离子形成的势场的阻碍，这种阻碍的大小可以用离子扩散活化能表示。对材料中离子输运的计算方法可分为基于几何结构、基于成键配位和基于能量变化这3类。

离子输运性质的计算方法可分为图40 所示的三种：根据锂离子是在晶格中一定的几何空间里运动，因此可通过 Voroni-Dirichlet 等空间分析方法来判断晶格中是否存在锂离子可运动的通道；更进一步的方法考虑了锂离子在晶格中的成键情况，根据锂离子在晶格中键价失配度来判断锂离子的通道和势垒值, 这种方法基于半经验势函数，计算量小，对单个晶体结构仅需几分钟就可完成计算；最为精确的计算模拟方法是采用基于密度泛函理论(DFT)的量子力学计算, 结合过渡态理论或分子动力学方法，得到能量势垒低的迁移路径，这种方法计算精度高，但运算量大， 对于单个离子迁移路径，通常也需要若干小时至若干天的运算时间。显然, 运算量过大是限制计算方法高通量化的主要原因。

图40 计算离子输运性质的几类方法及对应的计算量

针对各种计算方法的特点, 我们设计了将不同精度计算方法相结合的高通量筛选流程。基于化学成键作用的键价计算程序可在数分钟内半定量地模拟出材料中的锂离子输运路径和迁移势垒,非常适合于大范围计算的高通量筛选. 基于 DFT的过渡态计算能准确地计算出离子输运的势垒, 但计算量大、耗时长, 适合于对单个材料进行深入研究. 基于此, 我们将不同精度的计算方法用于材料计算筛选的不同阶段: 首先依据材料的使用条件通过元素筛选缩小范围, 然后采用快速的键价计算进行初步筛选去除离子输运势垒较大的化合物, 最后采用基于密度泛函的模拟对上一步筛选得到的材料进一步精确计算获得最终的备选材料, 从而有效地提高了整体的筛选效率, 实现了锂二次电池材料中快离子导体的高效筛选.

4.2. 键价和方法在锂离子电池研发中的应用

中国科学院物理研究所李泓等人将实验方法与理论计算相结合介绍了一种简便的湿混合方法，可以将超细AZO纳米粒子均匀地包覆在LCO粒子上。AZO改性LCO在4.5 V( http:// vs.Li/Li+ )高压半电池显示出较佳的循环寿命和倍率性能。通过扫描电子显微镜(SEM)，能量色散x射线能谱(EDS)，透射电子显微镜(TEM)、X射线光电子能谱(XPS)、X射线衍射(XRD)等表征手段分析表面改性及电化学性能之间的相关性。此外，通过低阻仪、电化学阻抗谱(EIS)和键价(BV)分析研究了改性LCO的电子和离子传输性质。

在以前的研究中，AZO包覆正极材料后，正极材料的动力学性能得到改善，原因归因于AZO具有较高的电子导电性，但Li+运输特性对AZO的贡献尚不明确。采用BV方法作为一个半定量工具用来评估锂离子迁移途径和活化能，锂离子的扩散路径如图7所示，表3列出了Al2O3、ZnO和AZO的活化能。从计算结果可以看出，AZO具有类似的一维锂离子扩散通道，其活化能(AZO的活化能1.80 eV，ZnO的活化能1.75 eV相比)，比LCO(2.87 eV)还要低。相比之下，虽然Al2O3常作为一种包覆材料，但Li+系三维扩散途径，扩散活化能量高达7.14 eV，这将阻碍Li+的运输。基于这些结果，作者确认AZO是锂离子和电子的良好导体。

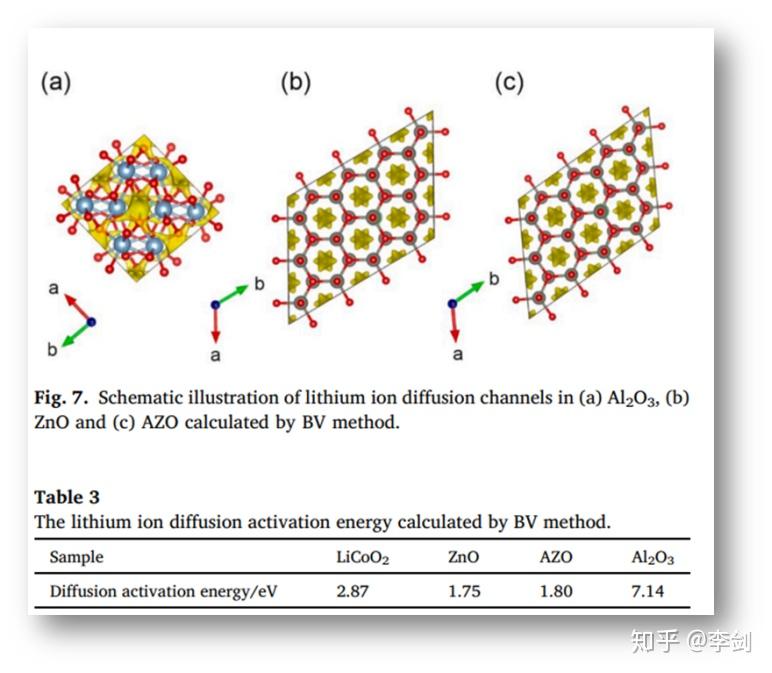
图45 BV法计算锂离子于(a)Al2O3,(b)ZnO和(c)AZO中的扩散通道示意图与通过BV法计算的锂离子扩散的活化能

其实BV方法还有很多经典的应用，详情请参考后文章节“8.高通量计算与数据挖掘在锂电材料领域的应用”部分。

4.3. 小结

需要指出的是，对于上述几种方法， 随着计算精度的提高，所需要的运算时间会大幅增长，如对于单一结构的计算，半定量的键价和方法的计算量在分钟量级，而基于DFT的第一性原理计算则往往耗时数小时甚至数天。因此，将各种不同精度的方法合理组合，用于材料筛选的不同阶段，是有助于提高筛选效率的办法。

5. 蒙特卡洛方法

5.1. 蒙特卡洛方法的介绍

蒙特卡洛方法（Monte Carlo，MC），又称随机抽样或统计实验方法，属于计算数学的一个分支，在20世纪40年代中期为了适应当时的原子能事业而发展起来的，学术界把1949年Metropolis和Ulam发表的论文作为MC方法诞生的标志。

知道物理规律，就能用蒙特卡洛方法模拟出满足物理规律的大量随机事件，由这些随机事件统计出需要计算的物理量的值。有些实验实施非常昂贵或非常危险，还有一些物理过程目前还无法探测，都可以用蒙特卡洛方法模拟出真实的过程。

5.2. 蒙特卡洛方法在锂电池中的应用

SEI膜对电池的安全性、循环性、首周库伦效率等有着重要的意义。Methekar等通过动力学蒙特卡洛模拟充放电过程中的副反应以及离子扩散等过程，观测到石墨表面SEI膜随着循环的次数增加而逐渐形成的过程。下图（a）表示首周循环后负极表面形貌，图（b）为100周循环后的负极表面形貌，红色表示SEI膜，品红表示处于原始状态石墨表面，黑色表示吸附了金属锂位点。

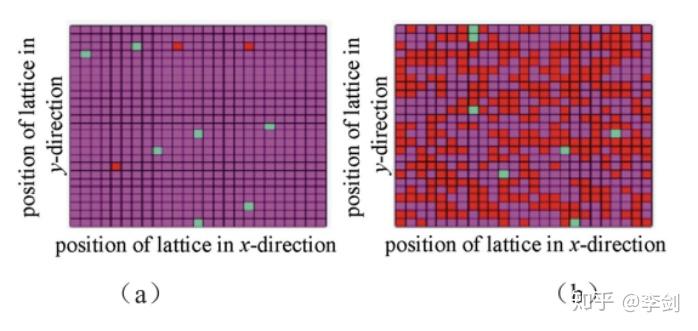
图46 模拟得到的负极表面在首周循环后（a）和100周循环后（b）的形貌

Ouyang等采用蒙特卡洛的方法模拟了LixMnO4在不同锂含量下材料的平衡态结构，计算了放电过程的电压，并模拟了升高温度后体系放电电压平台的变化，如下图所示。采用蒙特卡洛方法模拟了外电流和电压的关系，结果符合欧姆定律。

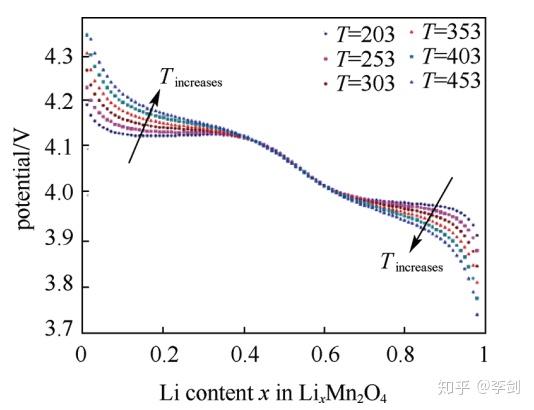
图47 模拟的LixMn2O不同温度电压平台的变化

Ouyang等还通过蒙特卡洛方法模拟了LiFePO4中掺杂Cr的情况，迁移出界面的Li+量随Cr含量变化，Cr含量越多，Li+量越少，电池容量越低，如下图所示。

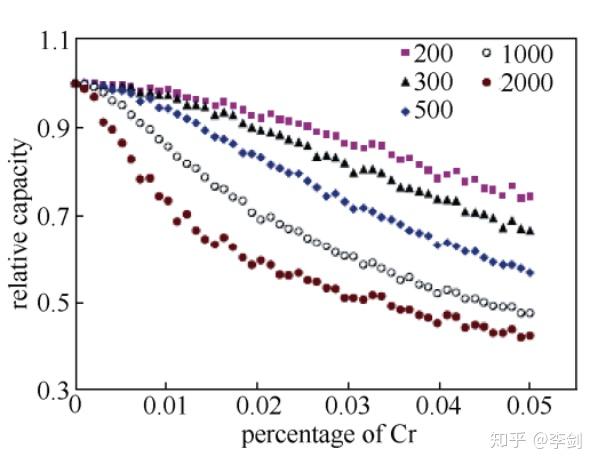
图48 不同Cr含量体系的可逆容量，200、300、500、1000、2000表示计算原胞大小

基于密度泛函理论的第一性原理计算能从电子结构的层面解释锂离子电池材料的结构、能带、缺陷、导电率、力学性质等本征特性，分子动力学和蒙特卡洛模拟等方法能在原子尺度模拟材料的动力学性能，上述方法都有助于理解材料在电化学过程中表现出来的种种现象。这些计算方法所关注的是材料在空间尺度为10-10~10-9m，时间尺度为皮秒量级的过程。如果需要考虑尺度在10-9~10-3m，时间在秒或者毫秒量级的问题时，则需要介观尺度的模拟方法。

6. 计算相图CALPHAD

6.1. 锂离子电池中的相图与相变

上文介绍了很多原子尺度的方法，接下来要为大家介绍介观尺度的方法，包括相场等方法，但是对于相场等方法是需要结合相图来协同工作的，相图本身除了对接相场外还有其他的用途，本章节主要介绍计算相图方法及其应用。

相变是电池材料基础研究中的重要问题。对材料相变的准确认识，有利于合成制备过程中获得晶体结构与组成符合设计要求的目标材料。了解电解质中的相变可以知道其使用的安全稳定条件，利用其相变性质发展新的电解质材料。相的组分与相变趋势可以由相图简明直观地展示出来。

充放电过程中电极材料的相变与材料的储锂机制、储锂容量范围、电压曲线、储锂动力学、材料的体积变化以及吸放热等密切相关。获得材料在充放电过程中的相组成、相结构演化及相图，对于全面理解材料及其充放电行为，开发新的电池材料体系具有十分重要的意义。

针对上述锂离子电池基础科学问题，李泓等人撰写了系列文章《锂电池基础科学问题（III）——相图与相变》与《锂电池基础科学问题（IV）——相图与相变（2）》，有兴趣的读者可以在网络上下载查阅。

6.2. CALPHAD计算相图发展史

传统绘制相图采用实验的方法，存在一些局限性。例如，测得一个相图需要庞大的数据；对于高温、低温时很难控制实验条件；高温等条件导致物质挥发，组分变化；化学分析时偏析造成的成分不均匀；测量也可能会干扰平衡条件。将热力学理论与计算机手段相结合，产生了新的交叉分支学科——CALPHAD（calculation of phase diagram，computer coupling of phase diagrams and thermochemistry），这是一种比较便捷绘制相图的手段。1908 年，Van Laar 将吉布斯自由能的概念应用于相平衡中，进行了数学分析；1957 年 Meijering尝试计算真实三元系统的完整相图；1959 年，Kaufman 用晶格稳定性和基于原子相互作用参数的正规溶液模型开始发展 Ti 和 Zr 二元系统相图的数据库，1967 年引入理想溶液模型研究非磁性过渡金属，又在 1968 年引入更多相互作用参数实现亚正规溶液模型；1970 年，Kuafman和Bernstein出版了第一本关于相图定量计算的教科书，标 志着CALPHAD 学科的建立；1973 年举办了第一届CALPHAD 会议；1975 年 CALPHAD 有限公司在马萨诸塞州成立；1977 年，美国国家标准局组织了关于合金和陶瓷相图研究的研讨会，同年，CALPHAD期刊由派格蒙出版公司出版，当年发表的文献包括Pettifor 的第一性原理和 Lukas 等的热统计学对相图计算的应用；1981 年 Sundman 和 Agren 等发展了Hillert 和 Staffansson 的亚点阵模型，并发展出Thermo-Calc 软件；1981 年以后提出了更多的模型和计算软件，并建立了相图热力学数据库。

6.3. 第一性原理相图计算

第一性原理可以广泛地用来预测锂离子电池的多种性质，包括嵌锂电位、锂-空位的有序性、锂离子扩散 、过渡金属有序性、电子输运等。将这种方法应用于锂离子电池相图与相变的研究，已经取得一些成果，包括新电极材料的筛选和开发 、多相材料的结构优化、对于不同实验条件或使用条件下的相稳定性和热稳定性 、反应路径和分解路径等。其中一些应用在上文已经提到。

Doe 等42利用第一性原理计算 Li-Fe-F 相图。下图(a)为其三元相图，并标识出不同三角相区的化合物相对于锂金属的电位；Doe 等对相图中超过100个点进行计算，探索不同化学计量比化合物的可能结构以及相稳定性，并预测了一些新型稳定化合物，其中实心圆点为稳定相化合物，“×”是亚稳相化合物。下图(b)为 FeF3 的扭曲的钙钛矿结构（ABO3，A 为空位），下图(c)为 FeF2 的金红石结构。下图(d)为图(a)的局部相图，并明确标出每一个稳定相的具体化合物，其中红色为钙钛矿结构，蓝色为金红石结构，绿色为钛铁矿结构，灰色为尖晶石结构，LiF为岩盐结构。下图(e)～(g)分别为 Li3/4Fe3/4F3（Li-Fe离子交换的金红石结构）、Li3/2Fe1/2F3（刚玉/钛铁矿结构）、Li15/8Fe3/8F3（尖晶石结构）。

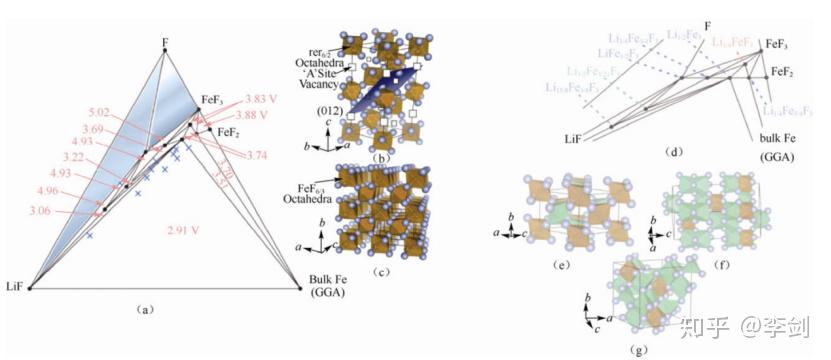
图49 （a）Li-Fe-F 三元相图；（b）FeF3（c）FeF2 的结构；（d）相稳定点所代表的化合物及（e）Li3/4Fe3/4F3（f）Li3/2Fe1/2F3（g）Li15/8Fe3/8F3 的结构

下图(a)、(b)为 Fe 块材的电压曲线和反应路径，由于反应有金属 Fe 的析出，且 Fe 的氟化物和 Fe金属电子态变化很大（分别为局域的 3d 电子和非局域的电子）。将金属Fe的化学势利用反应FeF2+2Li→Fe+2LiF 进行简单修正，得到下图(a)红色虚线所示的理论电压曲线，其化学势依然高于实验所得。

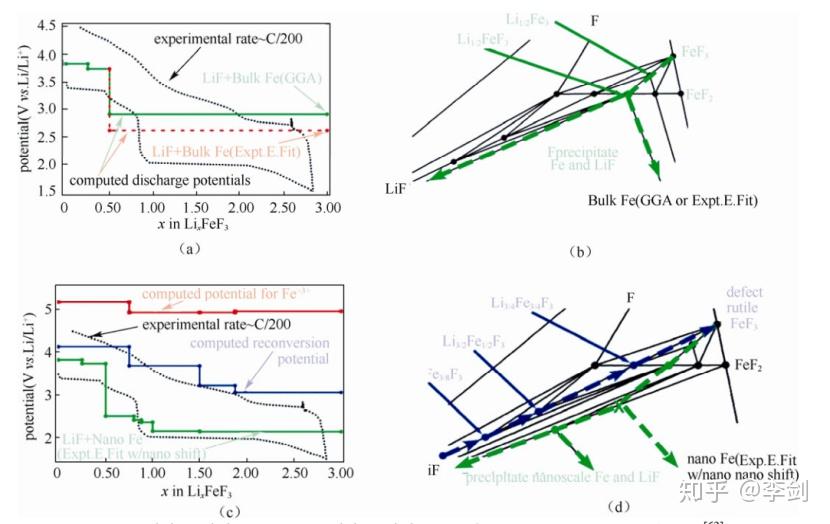
图50 （a）（b）Fe 块材；（c）、（d）Fe 纳米颗粒的电压曲线和反应路径

用1 nm的球形Fe颗粒替代块材，其能量增加，因而 FeF2 优先于 Fe 生成；假设反应过程中生成除FeF2 以外的 Fe2+亚稳相，包括 LiFeF3 和 Li2/3Fe3/4F3，反应路径如图(d)绿线所示，对应于图(c)的绿色放电曲线。以互扩散模型解释亚稳相的形成：Fe比Li更难扩散，为了补偿嵌锂过程中 Li 扩散入（而Fe来不及扩散出）化合物中所增加的电荷，Fe 离子倾向于成为低价态（+2 价）。此反应动力学上更容易发生。同理，在脱锂过程中 Fe离子倾向于+3 价，反应路径如图50(d)蓝线所示，且得到Li3/4Fe3/4F3、Li3/2Fe1/2F3、Li15/8Fe3/8F3 三种稳定化合物[如图17(e)～(g)所示]；反应对应于 18(c)的蓝色充电曲线。此结果展现了嵌锂电位与颗粒尺寸的关系，并解释了实验中“电势滞后”现象。

另外，在研究过程中还发现了其中金红石结构的 Li3/4Fe3/4F3 脱锂后容易得到三金红石（trirutile）结构的 FeF3，此结构的能量仅比稳定态的钙钛矿结构略高，且纳米尺度样品的 XRD 谱图与金红石结构的FeF2类似，这解释了实验中在完全脱锂后会形成类似 FeF2 结构的原因。

6.4. 相图的高通量计算

基于上面提到的第一性原理计算并结合晶体结构数据库，目前由麻省理工学院 Ceder 教授研究组对锂离子电池大量电极材料进行了高通量第一性原理计算，这种研究材料的方式被其命名为“材料基因组计划”（material genome initiative，MGI）。

其工作原理如图51(a)所示，。首先根据已有的晶体结构数据库建立概率密度模型；之后在任意一个 A-B-C 系统中，利用这一模型来识认相图中 某一化学组成是否能形成复合物[如图51(a)中红点所示]，这一化学组成的复合物可能对应着多种结构[如图51(a)中 1,2,3 三种结构]；最后，利用更准确的能量模型，例如密度泛函理论（DFT），选出复合物的最稳定结构。图51(b)是利用此方法预测的A-B-O 体系中不存在于 ICSD 数据库的新型化合物。图51(c)是在图 19(a)基础上，对元素进行取代并根据取代的概率模型计算结构的稳定性并判断电荷的平衡性，以此来预测新型的取代复合物。图51(d)标识了离子对的相关性程度gab，即一对元素相互取代的趋势。

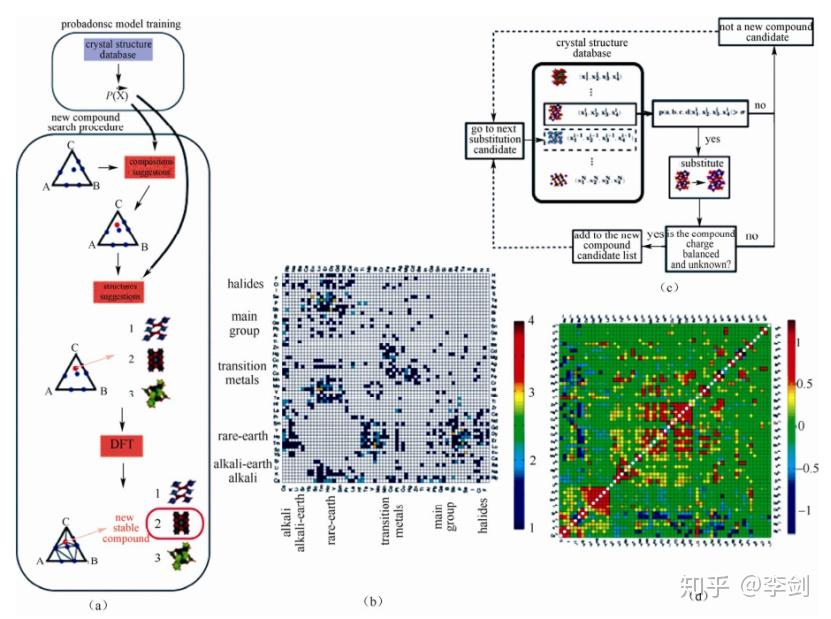
图51 （a）复合物开发程序的数据挖掘机制；（b）预测的新型 A-B-O 复合物；（c）取代的概率模型预测新型复合物；（d）离子对相关性程度 gab

Ceder 团队建立了高通量计算结果的数据库，截至2013年6月5 日，已计算30758种材料、3044个能带结构、438种嵌入电池以及 15175种相转变反应电池材料体系。数据库还在继续更新。这一数据 库可以通过网页进行查询（ http://www. materialsproject.org/ ），其部分应用如图52 所示。图52(a)为Li-Fe-P-O 相图，可以查询到 40 种稳定复合物（红点所示，包括 LiFePO4）和 178 种不稳定物质以及它们的生成能、分解能和物质编号。图52(b)为 Li-Fe P-O 复合物中，平均电动势在 3～4 V，容量>100 mA·h/g 的材料，给出的信息包括材料的编号、化学式及含 Li 量范围，电池类型（嵌入电池）、空间群、平均电压、质量比容量和体积比容量、质量能量密度和体积能量密度等；并可以在此界面中查找材料的电压曲线，如图52(c)所示。图52(d)为 LiFePO4 的细节，包括电池信息与结构信息。

图52 Li-Fe-P-O 的（a）相图；（b）平均电动势在 3~4V，容量>100mA·h/g 的复合物数据库；（c）电压曲线；（d）540081（LiFePO4）的详细信息( http://www. materialsproject ·org)

相对于实验，高通量计算基础上形成的相图有利于判断实验相图的完整性，挖掘在一类材料体系中迄今未知的化合物。但目前由于第一性原理计算方法对强关联材料体系的计算还存在较大的困难，计算时人为的因素较多，因此高通量计算相图主要适合于局域电子结构的材料体系。此外对于非整比化合物，由于计算时涉及的单胞较大，原子数较多，基于第一性原理的计算方法同样存在较大的困难（随着国内软件企业的发展，构建大体系的计算材料体系已经不成问题了，这一问题得到了解决。采用Nanodcal与RESCU等软件可以在保持高精度计算的前提下，实现数千乃至几万原子的计算。所以上述提出的问题可以得到解决。），仍需要与高通量实验方法相结合。理想的处理过程可能是首先通过第一性原理计算确定主体化合物，然后在该成分附近通过高通量制备、测试、表征，进而了解非整比、掺杂等产生新的衍生材料。在确定组成后再结合精细的计算方法进行理论验证。

关于高通量和材料基因组技术在锂电领域的应用，详细内容可以参考后文高通量计算章节。

6.5. 小结

电池材料在制备与充放电过程中的相与相变的研究，准确完备的相图的获得对于开发、设计、优化电池材料具有十分重要的意义。高通量的计算、制备、表征技术已经开始在锂离子电池材料研究中获得应用，普及后将会大大加快新相材料开发及相图绘制的速度。高空间分辨率、时间分辨率、能量分辨率的技术也被广泛的应用于电池材料的体相、表面相、界面相结构、组成及其演化的研究。锂离子电池中的相变与相图方面的知识虽然还远未完善，但正日渐积累。从原子尺度到宏观尺度了解相变过程、相变的驱动力、相的稳定性、相变对电化学性能的影响；获得除了组成相图之外，包括温压相图及各类物理性质的相图，相信已经为期不远。这些努力对于材料基础科学的发展以及储能材料的开发一定具有积极的推动作用。

7. 介观尺度模拟

介观尺度指的是介于原子层次和连续体之间的区域，在这个空间尺度里主要关注的微观组织结构随时间发生的演化，如晶体的生长凝固过程等，常用的模拟方法有相场方法，分子力场方法等。

7.1. 相场模型

相场模型可以用来处理纳米和微米尺度的结构演化，在该尺度范围内，材料的尺寸、形状、空间分布对材料的物理性质和化学性质起着重要的作用。微结构演化时间是自由能减少的过程，材料的自由能是体相化学能、界面能、弹性应变能、磁性能、静电能以及外加电场作用能的共同贡献。相场模型是建立在界面扩散的基础之上，微结构随时间的演化是连续性方程，即Ginzburg-Landau方程。相场方法模拟的介观尺度的现象包括晶粒生长和粗糙化、材料成型、裂纹演化、位错和溶质的相互作用、电迁移和多组分扩散等过程。这些过程在锂离子电池中都可能发生，并直接影响电池的循环性、倍率性、安全性等。

通过相场方法虽然能够模拟晶体生产、固态相变、裂纹演化、薄膜上的相变、离子在界面处的迁移等，但是模拟结果缺少和时间观测的定量比较，计算时界面厚度的设定通常大于实际情况，导致细节的缺失。

7.1.1. 相场方法在锂电池研究中的应用

Yamakawa等通过相场方法模拟层状正极材料LiCoO2不同晶粒大小、不同晶粒取向对Li+扩散的影响。下图所示为模拟得到的在恒流放电时LiCoO2中Li浓度的空间分布。显示出Li+的扩散对晶界、晶体方向的空间分布及晶粒的尺寸都十分敏感。

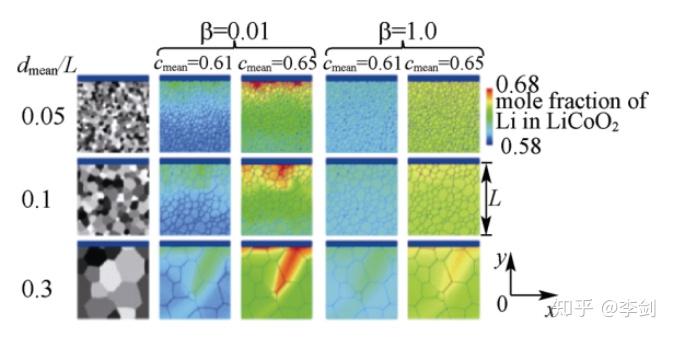
图53 模拟得到在恒流充放电条件下LiCoO2中锂浓度在不同颗粒尺寸（dmean/L）及不同晶面的扩散系数比值（β）下的锂Li+浓度分布

锂离子电池中还有很多现象可以通过相场模拟获得进一步的认识。如在纳米硅负极材料的充放电过程中伴随着材料体积膨胀，会导致黏结剂的脱落，SEI重新生成和容量衰减，Zuo等通过相场模型研究硅薄膜在嵌锂过程中力场分布以及裂纹的演化过程。

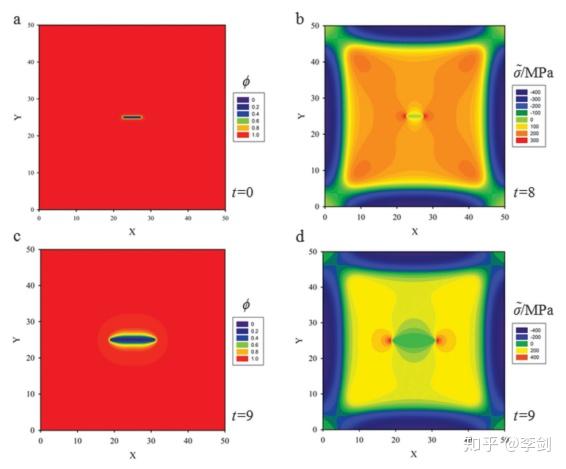
图 单直裂纹在扩散下扩展

7.2. 分子力学

分子力学，也叫力场方法（force field method），常用于计算化学和生物大分子等的结构和能量，也可以用于研究锂离子电池中的电化学过程。

7.2.1. 分子力学方法的介绍

分子力学方法中，在考虑几何结构或力学特性等静态性质时，将原子与原子间的相互作用视为主要的相互作用。因此在分子力场模型中，把组成分子的原子看成是由弹簧连接起来的球，然后用简单的数学函数来描述球与球之间的相互作用。

构成一套力场函数体系需要有一套联系分子能量和构型的函数，还需要给出各种不同原子哎不同成键状况下的物理参数，如正常的键角长、键角、二面角等，都是通过拟合特定分子的数据而生成的，这些被拟合的分子称为训练基（training set）。这些力场参数多来自实验或者量子化学计算。由于力场参数是拟合训练基分子得到的，并且所拟合的实验数据是常温常压下测量的，所以这些参数用于计算其他分子或者高温高压情况，分子力学的准确性会降低。

7.2.2. 分子力场方法在锂电池中的应用

Garofalini等利用分子力场方法研究了锂离子电池里，当金属锂嵌入纳米材料FeF2发生转化反应的作用机理。通过综合利用合理的经验势函数模型以及相关参数模拟FeF2+2Li=2LiF+Fe相转变过程中的动力学过程，图（54）显示了在FeF2（001）表面上发生的反应过程。图中Fe原子、F原子和Li原子分别用绿色、黄色和红色表示，整个FeF2表面上有4320个原子这4幅图分别表示有72、288、360、864个Li进入FeF2表面进行相转变的过程。可以明显地看到随着越来越多Li进入，金属Fe团簇和晶体状的LiF都在各自形成。

相场方法和分子力场方法可用于研究微观结构及其其演化过程对锂离子电池性能的影响，对于更大空间尺度上（10-6~100m）的问题，体系的随机性不明显，可以采用下文介绍的基于连续体模型的宏观尺度模拟方法。

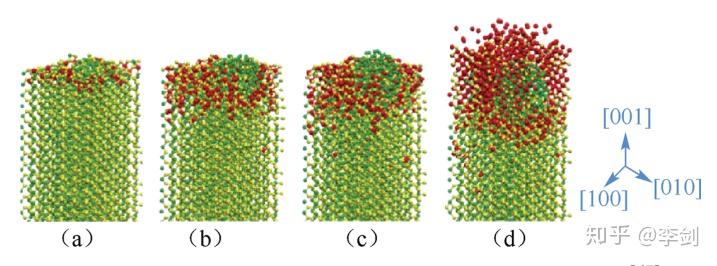
图54 模拟得到Li在FeF2（001）表面的反应

8. 宏观尺度模拟

在宏观尺度上，体系的运动力学遵循牛顿力学方程，热运动满足宏观的扩散方程，可以采用的数值模拟方法包括有限元方法、有限差分法等，其中有限元方法常用来研究锂离子电池中的热流分布、应力分布等现象，本节将主要介绍有限元方法及其在电池材料研究中的应用。

8.1. 有限元方法介绍

有限元（finite element method）是一种求解偏微分方程编制问题近似解的数值技术，如何求解电池内部的热、力、电流、电压的分布等都需要求解在特定边界条件下的输运方程。而这些方程的精确求解几乎是不可能的。人们通常采用两种方法去逼近真实的解：全域的展开逼近，典型代表为傅里叶级数展开；基于子域的分段函数展开，如有限元。后者将求解域看成是由许多简单而又相互作用的元素的互连子域组成（单元），对每一单元假定一个合适的（较简单的）近似解，然后推导求解这个总域满足条件（如结构的平衡条件），从而得到问题的解。这两种方式各有特点，全域的方法采用高次连续函数通过几个基底函数得到很好的效果。第二种方法要通过较大的工作量才得到较好的效果。但是能将复杂方程的解化繁为简，使得描述和求解成为可能。

8.2. 有限元方法在锂电池研究中的应用

对于高功率的动力电池而言，电池内部温度分布对其安全性和寿命有重要影响。西安交通大学曹秉刚等在考虑内阻、对流、外部耗散等条件下利用有限元方法模拟了电池工作时内部温度的空间分布，以及在155℃热炉中测试电池的温度分布（图55），模拟结果和VLP50/62/100S-Fe（3.2V/55A·h）LiFePO4/石墨的电池复合。

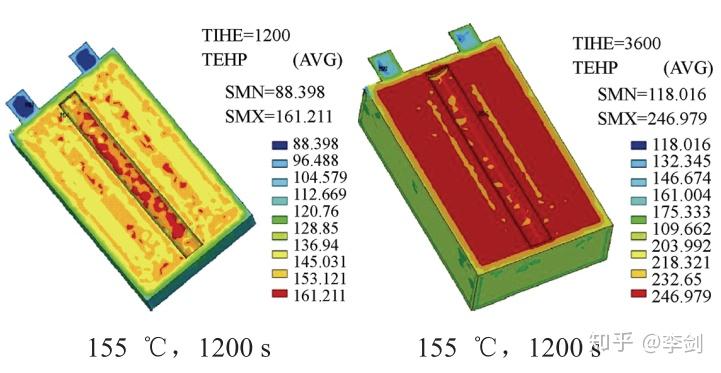
图55 有限元模拟在155℃，1200s和3600s温度在电池中的分布

Bower等利用有限元的方法研究了嵌锂后硅颗粒内力分布。图22显示了采用有限元方法模拟的薄膜非晶硅电极在充放电循环过程中的应力分布及形变和断裂过程。

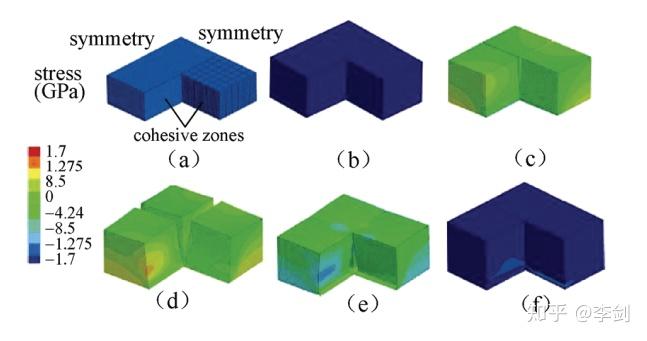
图55 非晶薄膜Si电极在充放电循环过程中的断裂，变形和应力分布

宏观尺度的材料模拟着眼于工程领域的问题，可以有助于理解锂离子电池中出现的应力、传热、流动以及多场耦合等宏观现象。

9. 高通量计算与数据挖掘在锂电材料领域的应用

先进电池技术是未来十年世界各国前沿技术竞争的制高点。锂电池由于具有电压高、比能量高、充放电寿命长、工作温度范围宽等优点，已成为许多移动电子产品、电动汽车以及风电和光伏电储能的首选。 因此更快的开发出能量密度高、安全性好、充放电速度快的高性能锂电池材料十分必要 。

9.1. 高通量计算发展概述

在锂电池材料设计开发的过程中，采用高通量计算的理论方法始于MIT的Ceder研究组，他们从2010年开始开展了称之为(锂离子电池材料基因工程)的研究。该方法通过对含聚阴离子XO4（X=P，S，As，Si）的化合物中元素的替代，来产生新化合物，计算了其能量密度、电压、 脱Li后的体积变化等参数，据此筛选新材料。他们从自然界存在的矿物Sidorenkite结构出发，对其进行元素替换， 构造出270多种组分和结构，并计算其性能，从中筛选出了几种材料Li3Mn（CO3）（PO4）、Li2V（CO3）（PO4）、Li3V（CO3）（SiO4）

等。应用类似办法，他们还对含有（PmOn）阴离子团的各种过渡金属与Li的化合物进行了筛选。 同时，在上述研究过程中，他们也初步发展了一套系统的性能计算、数据生成、数据分析的办法50。日本的Tanaka研究组将第一性原理分子动力学模拟与机器学习技术相结合" 研究了LISICON类型材料的离子输运，通过将理论计算结果与实验数据库结合，可有效预测LiO1/2—AOm/2—BOn/2体系不同组分的离子电导率，有助于加快固态电解质的开发。

上述研究工作中所用到的高通量计算方法都具有图1所示的共同特点。首先从外部的结构数据库中选择数据，产生可被计算软件调用的输入文件，并进行计算得到材料相应的性质数据，运算结果保存到数据库以备进一步的分析，获得的新知识可扩充原先的数据库并有助于更为准确的数据选择。由此可见，形成并完善一套程序化的高通量计算流程" 把各种计算软件包、编写的单一功能的计算程序或指令（如输入文件生成& 、材料性质模拟、结果分析程序等）和计算硬件设备等关联起来，使得整个过程能够自动完成，是实现高通量计算提高整体效率的关键。上面提到的由Curtarolo等人设计的ALFOW和由Cedre小组设计的计算流程均实现了晶体结构数据库与第一性原理计算程序VASP的自动调用功能，从而通过高通量计算获得材料的形成能等热力学数据以及电子结构的信息。但由于筛选不同类型的材料时所关注的性质往往是不同的，希望调用的材料数据库、模拟方法、分析方法都可能有所变化，所以针对各种不同的材料还需设计相应软件以实现特定的自动化运算流程。

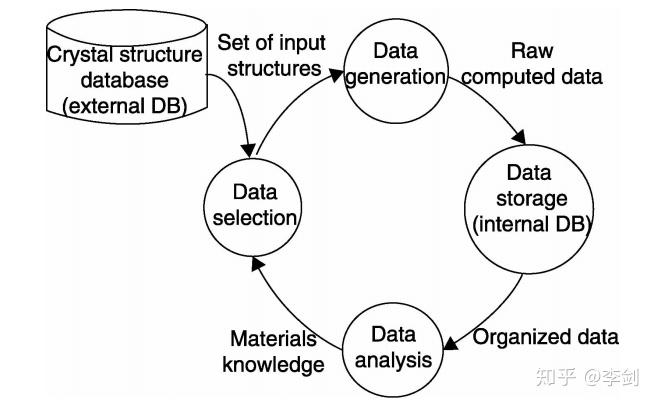
图56 高通量计算筛选材料的数据流程图

目前对于锂电池材料的高通量筛选，国内外的研究工作都处于起步阶段" 尚存在以下问题：（1）偏重于材料热力学性质，如形成能、热稳定性等的计算，缺乏对锂离子输运这一重要的动力学性能的考虑；（2）筛选所用的约束条件缺乏针对性和层次性，造成大量重复及不必要的计算；（3）计算采用的多是基于密度泛函的第一性原理方法，尚未结合其他更多的计算方法或软件；（4）对计算得到的大量数据尚未进行有效的挖掘。事实上，材料的性能完全由材料的结构和组分两个因素决定，通过大规模的计算，挖掘出材料结构、组分和材料性能之间的联系。构建出材料的(构效关系)，也是高通量计算的重要目标之一。通过对筛选过程设立有针对性的外部约束条件，包括应用要求约束、基本物理规律约束、温度压强等外部条件，构建材料组分和结构模型。通过高通量计算技术来计算这些结构模型对应的化合物的各种性能，并反馈到结构性能数据库，用于研究锂电池材料中的物理问题，同时筛选出满足应用约束条件的材料。并通过各种实验方法制备这些材料，然后测试和表征这些材料的物理化学性能，最终达到理解锂电池材料物理问题，并发现新材料的目的。可以预见在未来几年内，应用高通量计算方法，结合实验研究， 将大大加速我们对锂电池材料的研发，加深对锂电池中各种问题的理解" 揭示材料的结构-性能关系及内在物理规律，从而缩短材料从研发到应用的全过程。

9.2. 富锂正极新型包覆材料的筛选

在全固态电池中, 电极/电解质界面的稳定性和离子电导率都影响着电池的整体性能。在电极表面包覆上能传输锂离子并阻隔电极、电解质之间发生反应的化合物往往能改善电池的综合性能。若包覆物与电极具有相似的晶体结构, 将更易于形成结合紧密、应力较小的界面层。从高通量计算筛选的1000多种含锂氧化物中, 不仅能发现离子输运势垒较低的快离子导体备选材料, 而且还发现了一些与目前所研究的电极材料具有相似结构并且能传导锂离子的化合物, 这些化合物有可能用作电极的包覆材料, 从而改善电极的综合性能。

基于材料基因组思想，通过采用高通量计算筛选，综合考虑结构匹配、扩散通道、导电性等因素，发现了两种可能与锂离子电池富锂正极材料相匹配的包覆化合物 Li2SiO3和Li2SnO3。这两种材料都属于离子化合物，具有较好的离子导电性，并且在化学结构上与富 锂材料((1−x)Li2MnO3·xLiMO2)中的母相材料Li2MnO3相似，因此可尝试选择其作为富锂材料的表面修饰层。

下图展示了Li2SiO3和Li2SnO3的晶体结构及采用键价方法计算得到的离子输运通道，可以看出它们具有与Li2MnO3相似的层状结构及二维离子输运通道。

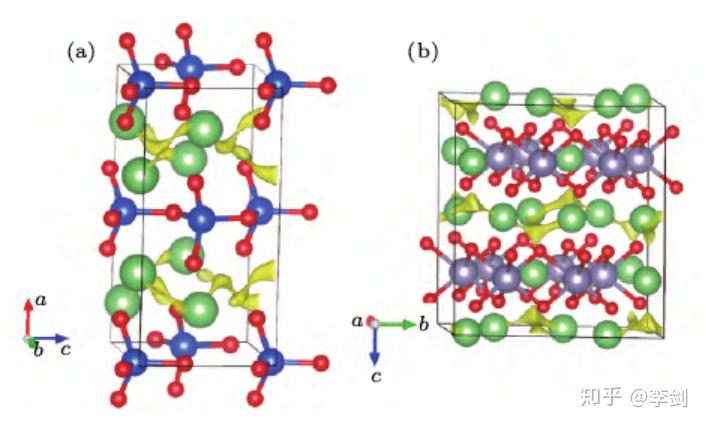
图57 用键价方法计算得到的（a）Li2SiO3和（b）Li2SnO3的离子输运通道

通过实验制备包覆后的富锂正极材料并测试其电化学性能，证实了包覆材料Li2SiO3和Li2SnO3可有效改善Li2MnO3电极的循环稳定性。对比包覆前后电极的循环伏安曲线、交流阻抗谱等实验结果, 发现包覆的主要作用是加速了电极扩散速度，抑制了循环过程中界面阻抗的增大，从而改善了电极的反应动力学。其中 Li2SiO3修饰后的材料在表面会与电解液发生化学反应，生成路易斯酸。生成的这种强酸一方面能够加速过渡金属离子的溶出，中和材料表面的碱性绝缘杂质，另一方面形成的表面固溶体有利于表面锂离子的扩散，使材料表现出更好的电化学性能和结构稳定性。而Li2SnO3为修饰层的材料在活性材料表面作为保护层不仅能够保护材料免受电解液的腐蚀, 抑制过渡金属离子的溶出, 而且提高了材料的动力学行为, 从而使材料具有较好的电化学性能。

9.3. 高通量计算筛选固体电解质β-Li3PS4的优化改性方案

目前从改善锂二次电池安全性的角度考虑, 全固态锂电池被公认为未来二次电池的重要发展方向。在传统的锂二次电池中，电解液体系采用了液态可燃的有机溶剂，而全固态锂二次电池则采用稳定的固态电解质材料，有望从根源上改善电池的安全性问题。此外，在全固态锂二次电池中，有可能采用金属锂作为负极材料，而金属锂负极的理论容量是锂电池体系的最高极限，其电位也是所有负极材料中最低的，因此可以大大提高锂二次电池体系的能量密度。然而，使用固体电解质材料体系的一个最大问题是锂离子在固体电解质材料中的离子输运很慢。一般来说，锂离子电导率在固体电解质中要比在液体电解液中低 1—2 个数量级。开发兼具高离子电导率、高稳定性、高机械强度的固体电解质材料势在必行。

在已经研究过的固态电解质材料中，硫化物作为目前发现的具有最高锂离子电导率的固体化合物，一直是研究中的热点。然而硫化物在空气中的敏感性以及它在与氧化物正极界面处表现出的化学不稳定性，极大地限制了硫化物在固态锂电池中的实际应用。Li-P-S 体系是目前发现的稳定性最高的含锂硫化物体系，对该体系中的组分进行改性优化，有望在提高其离子电导率的同时进一步提升其稳定性，从而获得新的固态电解质备选材料。通过采用密度泛函计算与键价计算相结合的方法，可以对大量的掺杂改性方案进行高通量的计算筛选。采用可准确确定晶体结构的密度泛函计算来获得掺杂后的原子位置信息，再通过键价计算快速选择其中有利于降低锂离子迁移势垒的掺杂方案。通过对β-Li3PS4的P位进行Sb， Zn，Al，Ga，Si，Ge，Sn 的掺杂，以及对S位进行O掺杂的研究发现, 用氧替换晶格中部分硫或用锌氧两种元素对 β-Li3PS4进行共掺杂能有效提高其离子电导率(图58 )3。进一步关于其稳定性的计算表明, 氧的掺入提高了β相的稳定性，降低了该材料在室温附近向γ相转变的趋势 。

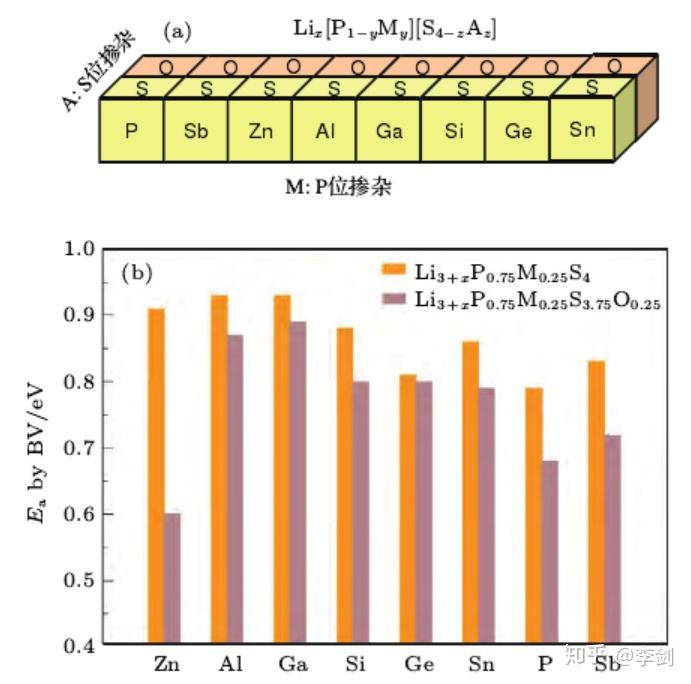
图58 （a）采用密度泛函计算与键价计算结合的高通量计算流程，筛选能改善β-Li3PS4离子电导率和稳定性的掺杂改性方案；（b）P位掺杂Sb，Zn，Al，Ga，Si，Ge，Sn以及S位掺杂O后计算得到的锂离子迁移势垒

在通过高通量计算筛选获得了材料改性的优化方案后，基于密度泛函的高精度计算可有效揭示掺杂对材料性能的改善机理。计算得到的电子结构表明上述性能的改善来源于 P—O 键与 P—S 键之间的差异。氧掺杂 β-Li3PS4引起了 [PS4]3−单元局域结构变化，在掺杂单元 [PS3O]3−附近提供了更多供锂离子运动的空间，形成了新的离子输运路径，使得原本的二维输运方式转变为三维输运方式。对β-Li3PS4与金属锂界面的模拟显示，与锂接触的 [PS3O]3−单元虽然发生显著的形变，但并未发生化学键的断裂，从而稳定了两者的接触界面。

9.4. 高通量结构预测方法发现全新结构的固体电解质LiAlSO

在通过高通量计算筛选固体电解质β-Li3PS4优化改性方案的过程中，氧掺杂显示出了对硫化物稳定性提升的显著效应。在目前探索的固体电解质材料中，氧化物和硫化物均显示出各自的优势。与硫化物相比，氧化物具有更高的稳定性，也更加容易制备，然而其离子电导率仍然远低于硫化物。而硫化物虽然具有较高的离子电导率，但使其稳定存在的条件更为苛刻，且制备过程更为困难。考虑到硫化物和氧化物各自的特点，我们提出了设计多种阴离子共存的快离子导体设计思想，并尝试设计含锂的氧硫化物，以集成硫化物高离子电导率和氧化物高稳定性的优点。

高通量结构预测算法可用于在已知元素组成的空间里设计全新的晶体结构，该方法已成功应用于高压条件下新型化合物的寻找。通过采用CALYPSO 软件在 Li-Al-S-O 的元素空间中构建具有各种空间群的晶体结构，并对其进行结构优化和能量计算, 基于其中能量低的结构运用粒子群优化算法生成新的结构，在此优化过程中，逐渐找到由这四种元素按照 1 : 1 : 1 : 1 的比例形成的最稳定结构。计算结果显示，这种全新的氧硫化物 LiAlSO 具有与 β-NaFeO2相似的正交结构，AlS2O2层沿 b 轴方向平行排列， Li 离子位于层间与S和O形成扭曲的四面体单元 (图 59 )。基于密度泛函的计算表明，Li 离子在该材料中沿 a 轴方向的离子迁移势垒低于 50 meV，是典型的快离子导体，因此，该化合物作为一种全新的快离子导体，可以成为固体电解质的备选材料, 并且兼具高离子电导率和改善的化学稳定性。

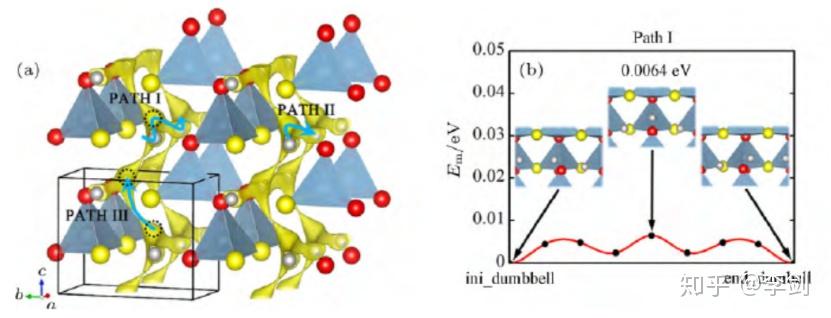
图59 （a）采用高通量晶体结构预测算法得到的含锂氧硫化物LiAlSO的晶体结构；（b）密度泛函计算得到的锂离子在该结构中的输运势垒

9.5. 数据挖掘方法研究零应变电极材料中结构与体积变化的关联

基于材料基因思想的高通量计算与高通量实验测试为新材料研发领域不仅提供了新的研究思路，而且带来了成倍增长的数据信息， 为大数据方法在材料学中的应用打下了基础。在电池材料中还存在许多尚未研究清楚的现象，探寻结构与性能之间的关联有助于建立起搜寻具有目标物性材料的快捷方法。机器学习技术已被用于获取材料性质与各种复杂的物理因子之间的统计模型，例如通过预测分子的原子化能寻找热力学稳定的新化合物。

在固态锂二次电池中，固态电解质/电极界面上的稳定性与电池的循环特性紧密相连，其中界面的力学稳定性主要由电极在脱嵌锂过程中的体积变化决定。电化学循环过程中，固态电解质的体积并不发生显著变化，而电极材料则在锂含量增加和减少的过程中会发生体积的变化，若体积变化过大，会造成固态电解质与电极之间接触界面的松散，影响离子在界面的传输。因此，寻找脱嵌锂过程中体积变化小的 “低应变”材料十分必要。基于第一性原理计算得到正极材料在脱锂前后的晶胞体积，以及根据晶体结构、组分、元素、电荷等信息提取描述因子，在此基础上尝试采用机器学习中的多元线性回归分析来寻找影响体积变化的主要因素，构建微观结构与体积变化之间的关联。

图60显示了采用数据挖掘方法研究目标变量与描述因子之间关联的三个主要步骤。首先需进行数据准备, 获得不同样本中目标变量的数据,这里针对尖晶石结构的正极材料LiX2O4和层状结构的正极材料LiXO2（X为可变价元素）共28种结构, 通过密度泛函计算对材料在脱锂前和完全脱锂后的结构进行优化, 获得由于脱锂导致的体积变化百分比。接下来需要对每个样本建立一系列描述因子, 用于表述其原子层面的微观信息, 由于并不清楚哪些因子与体积的变化有关, 因此列出了尽量多的描述因子, 期望通过数据挖掘模型的构建探寻这些因子与目标物性（体积变化）之间的关联. 在本研究中, 为每种结构选取了34个描述因子, 包括与晶格参数相关的 7 个参数、与组成元素基本性质相关的10个参数、与局部晶格形变相关的 12 个参数、与电荷分布相关的 3 个参数和与组分相关的2 个参数。在具备了描述因子与目标变量的数据后，就可开始采用数据挖掘的方法来建立因子与变量之间的关联，对于所建立的模型, 需要采用统计参数来评估其可靠性及预测能力，并在合理的预测范围内对新的结构进行目标物性的预测。

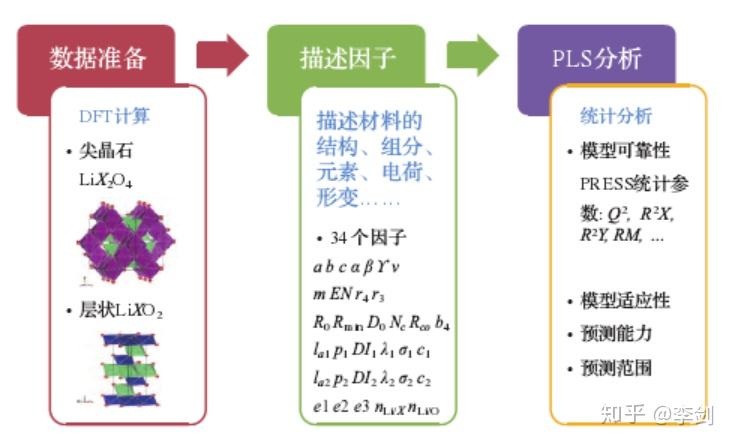
图60 采用多元线性回归数据挖掘方法分析脱锂前后晶格体系变化与结构之间的关联

通过采用 “Leave-One-Out”方法进行评估，发现在上述问题中采用11个相关变量 (11 components) 时得到的Q2指数最大，表明此时得到的模型最为稳定。进一步的因子重要性分析表明(图61 )，尽管离子半径是晶格体积变化的重要决定因素，但体积变化并不仅仅与离子半径有关，过渡金属的成键参数及过渡金属氧八面体的局域结构也对体积变化起到作用。在此模型的基础上，可以构建含有多种过渡金属的正极材料，共同调节体系在脱嵌锂过程中的体积变化，最大程度地减小由于锂含量变化导致的晶格体积变化率。

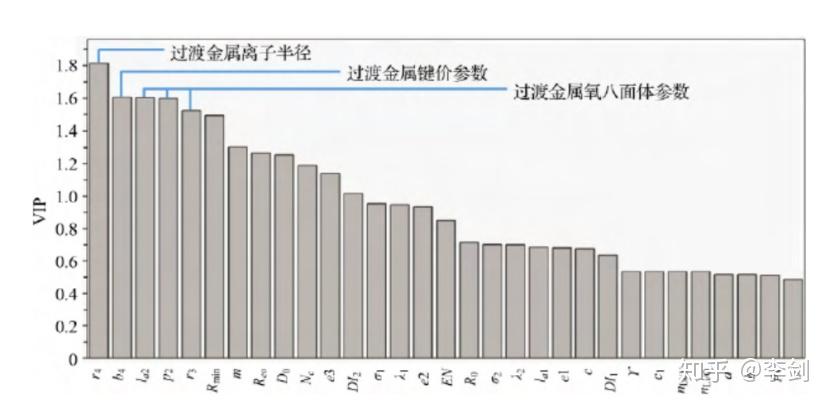
图61 采用PLS模型因子重要性分析探寻对正极材料脱锂过程体积变化影响较大的参数

9.6. 固体电解质离子输运特性数据库及其高通量筛选平台

上海大学施思齐教授团队基于材料基因组技术开发了固体电解质离子输运特性数据库及其高通量筛选平台。详细内容可以访问溧阳深水科技公司的深水科技公众号了解详细情况。

其具体框架如下图所示：

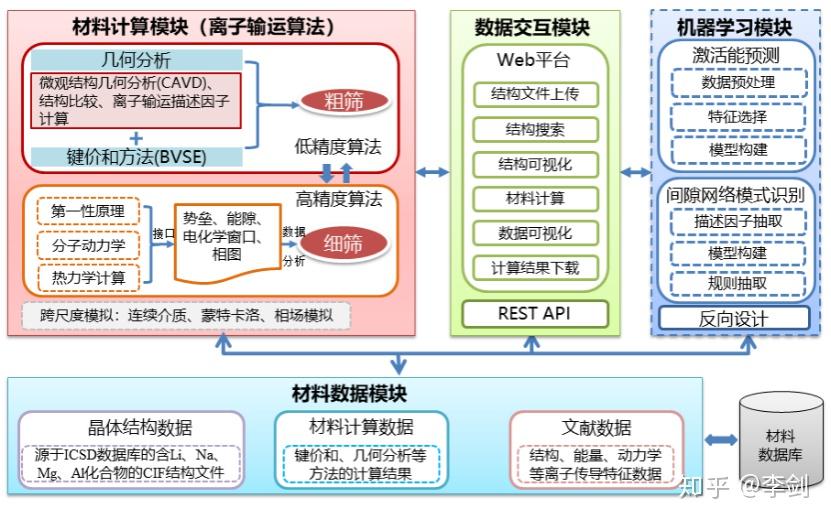
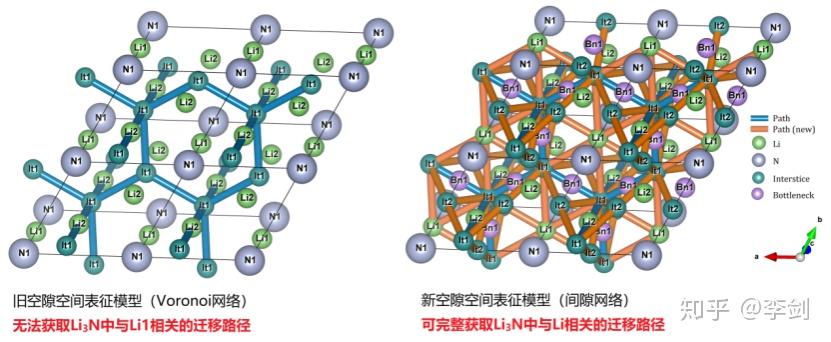
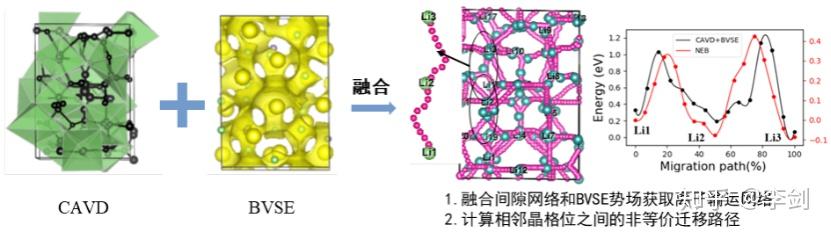
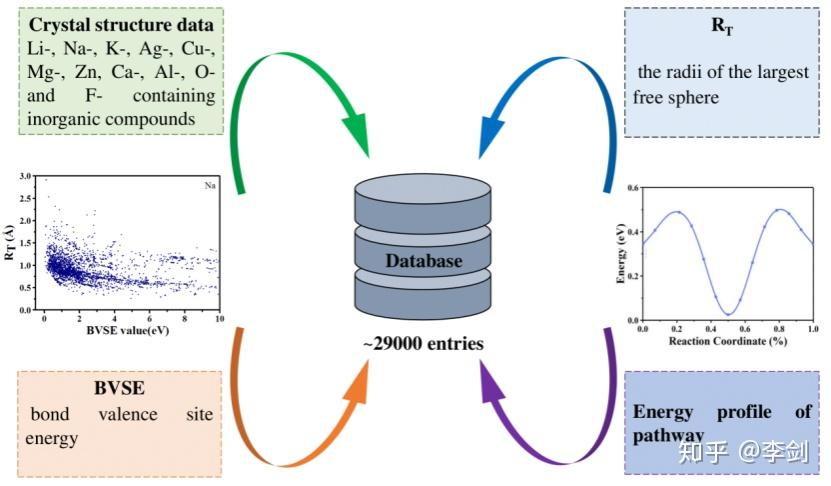
图62 (a)固态电解质筛选平台（SPSE）的架构；(b)旧、新空隙空间表征模型对比；(c)多精度融合算法原理；(d)离子输运特性数据库的架构。

9.7. 国产自主知识产权商业化锂电材料基因组软件FIRST

国内鸿之微科技开发了自主知识产权的商业化材料信息学软件FIRST，并通过该软件进行了固态锂离子电池电解质材料的筛选。

详细内容可以访问该公司网站：

（ http:// hzwtech.com/software-pr osubsub/263.html ）

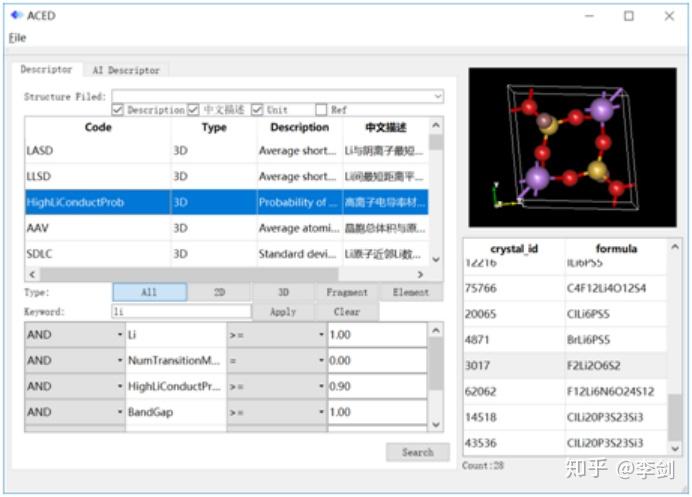
图63 筛选含锂的高离子电导率材料

1.1. 采用高通量计算搜索新型电解质添加剂

大量有效SEI添加剂的理论研究表明，高还原电位、高亲电性、相对偶极矩、低化学硬度等参量均可作为高通量筛选添加剂的描述因子。通过计算可以大大加快对新添加剂的需求。2009年，Han等人计算了108个有机分子的电离势和氧化势，以寻找具有高氧化电压的电解质。

对于还原反应，Halls和Tasaki在2010年筛选了7381种基于EC的结构。基于有效SEI形成所需的还原性添加剂的基本电化学性质的比较，可以使用许多描述符，例如HOMO，LUMO，电子亲和力（EA），相对偶极矩和化学硬度（η）。Halls和Tasaki提出了两种合适的SEI形成添加剂的筛选标准：低LUMO能量（高EA）和小η。 他们使用一种自动方法来生成基于氟和烷基衍生的EC的添加剂库（如图64a所示），然后使用高通量QC解决方案对衍生物进行分析和筛选，以寻找合适的添加剂。 基本工作流程如图64b.所示。图64c显示了一种很有前途的氟衍生EC。前面提到的已显示出改善的SEI性能的添加剂（例如FEC和BS）满足了这项工作中提出的描述。 请注意，FEC是在库中自动生成的。除了还原电位外，Park等人还提出，低Li +结合能是添加剂筛选的另一个描述因素，因为Li +-添加剂的结合能越小，则其去溶剂化就越容易。

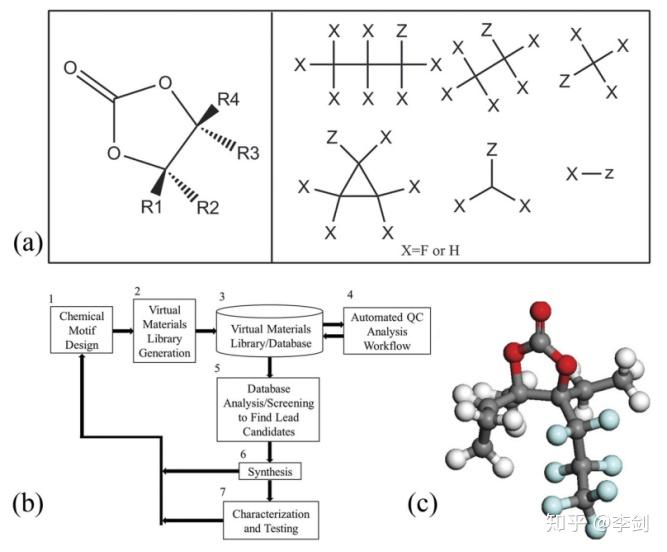
图64 为利用高亲电性及低化学硬度为描述因子对EC的含F衍生物及烷基衍生物进行的高通量筛选研究。a EC核心结构（左图）和R组结构（右图）用于枚举结构库，其中Z表示连接点； b筛选工作流程； c筛选出一种典型的高效添加剂，其配色方案与表1相同，F原子表示为浅蓝色（版权所有：Elsevier B. V.）

Delp等人强调了锂溶剂结合能在确定第一个溶剂化壳结构中的重要性。 他们使用了簇中的相对Li +-溶剂结合能-连续计算以及还原电位，以估计溶剂/添加剂进入Li +配位壳并进行还原的可能性。通过结合QC计算来评估热力学和动力学效应，Husch和Korth提供了一组描述符，用于考虑阳极SEI的形成和石墨剥落，从而筛选出新的电解质，这被称为“氧化还原指纹分析”（RFPA）。 计算电解质筛选的成功取决于这些关键指标。

计算电解质筛选的成功取决于这些关键指标。但是，这些描述符主要集中在初始SEI的形成和热力学上。正如我们在“纳米厚的SEI层的构建”一节中讨论的那样，可以描述从电解质还原形成数十纳米厚的SEI的基本理解和计算方法尚未得到充分发展。 因此，尚未确定这些初始还原过程如何控制SEI膜的组成和形态，更重要的是控制SEI膜的性能。 为此，需要开发多尺度的高通量计算方法 。

尽管如此，高通量量子化学分析和虚拟筛选正在彻底改变用于锂离子电池等设备集成设计的材料发现。 另外，为了满足具有高电压电极材料的先进电池，正在通过计算方法探索具有更宽电化学窗口的新型电解质。

9.9. 总结

应用高通量计算方法探索和设计锂电池新材料，是未来材料科学研究和开发的一条重要途径。借助无机材料晶体结构数据库中现有的和衍生的结构，设定合理的限制条件，有望筛选出下一代锂电池的备选材料。

应用高通量计算方法探索和设计锂电池新材料，是未来材料科学研究和开发的一条重要途径。借助无机材料晶体结构数据库中现有的和衍生的结构，设定合理的限制条件，有望筛选出下一代锂电池的备选材料。 从材料研发的角度 ，这种方法有可能从现有晶体结构中找到或构建出新晶体结构，并评估新结构存在的可能性以及作为锂电池材料的性能，更快找到高性能、高安全性的正极、负极与电解质材料，促进锂电池产业的发展" 加速锂电池材料的开发过程。

从基础研究的角度 ，高通量计算得到的大量数据，将有助于理解与锂电池有关的现象，如结构与离子扩散、储锂容量之间的本质关系。计算得到的晶体结构、电子结构和各种性质，与现有的实验数据汇集到一起，将形成一个庞大的数据库，为材料学家及物理学家提供全面

而宝贵的数据参考。进一步借助统计方法进行数据挖掘，还有可能找到决定材料性质的因，如相关的结构单元或是通过统计方法定义的关联函数等，从而找到背后的物理原因。

10. 总结与展望

10.1. 有望解决的关键问题

随着各种理论的完善和计算机技术的发展，计算模拟已经成为锂离子电池研究中的重要方法之一。不同时间与空间尺度的模拟方法有助于我们从原子分子层次、介观层次和宏观层次理解材料结构与性能之间的关系。而这些不同尺度上的计算方法可以通过参数传递进行联系，从而实现材料的多尺度模拟，为材料设计提供了一种新的途径。通过实验与理论计算相结合的方法，有望解决的锂离子电池研究中的关键科学问题如下：（1）设计出新的电极与电解质材料：找到一些目前尚未发现的锂离子电池材料，并且具有更好的性能与更高的安全性；目前正在发展的材料基因组方法是锂离子电池计算方面发展的重要方向。（2）理解体相电极材料反应的热力学问题，通过精确计算材料的反应生成焓，预测材料在各种条件，如不同温度、不同压力、不同组分下的稳定性，甚至建议材料的合成方案。（3）理解电位与材料组成、微观结构的关系。通过计算与实验得到大量已知结构及新结构所对应的电化学电位，建立电位与结构关系的数据库，采用统计方法，寻找决定电位的因素，理解它们之间的物理关联。（4）电极材料充放电过程中组成与结构演变，通过计算得到的生成焓数据，建立与电极变化过程有关的相图，分析电极材料结构演变相对稳定性的影响，理解影响电极循环性能的因素以及电极材料的失效机制。（5）与电池有关的复杂过程的理解，如输运机制，尺寸效应，界面问题等复杂过程。（6）材料与器件制备过程、服役过程的数字化模拟与仿真。

10.2. 第一性原理技术向大尺度计算方向发展

目前在锂电领域常规的方法主要包括了第一性原理、分子动力学方法、相场等各类方法，其中最被业界认可的计算方法为第一性原理计算方法，因为此类型的方法模型确定，相对于其他需要重新建立模型的方法而言，该方法不需要依赖实验数据，也不需要重新构建数学模型，但是常规第一性原理方法计算体系过小，无法对锂离子电池中包括：大缺陷、低浓度缺陷、掺杂、大尺度界面等实际的问题进行模拟，需要开发能够在保证企业投入较低的情况下，满足数据安全性等问题的大尺度的计算方法。目前全球主流的第一性原理软件主要分为开源和商业软件。其中开源的常见软件主要为：QE、GPAW等；商业软件主要有：VASP、Materials Studio、Nanodcal、RESCU等软件。

10.3. 开发更加快速的计算方法

工业界与学术界的需求不同，学术界可以在一定的时间范围内承受发表学术成果投入较长时间预算的压力，而工业界比较关注的问题是能够在较短的时间内获取计算结果，部分企业的要求甚至极高，要求计算方法与实验方法进行单次对比，获取更少的成本投入。

10.4. 锂电关键材料数据的积累和数据库

随着材料基因组技术的发展以及AI技术的发展，目前材料数据出现了爆发式的增长，部分从事材料科学研究的学者，甚至提出了材料研究从材料的大数据时代进入了材料的互联网时代。锂电材料数据的核心目标是为了能够建立精确和完善的材料结构与性能之间的模型。对于很多锂电企业而言，材料数据被其视为核心机密。全球每年会生产几百亿个电池，但是最终能够得到全面数据的也就是量产的，对于在研发过程中的很多电池而言，随着它们的夭折，其数据也就没有采集得那么全面。而对于采用材料基因组技术进行材料数据挖掘的用户而言，材料数据是核心。而在材料大数据或者材料基因组技术中对材料性质的描述所用的描述符（descriptor）是这些材料数据的重中之重。锂电材料既涉及到晶体材料，同时又涉及到不少的分子材料。因此，一方面需要借鉴化学信息学和生物信息学领域的QSAR技术的发展，同时需要在晶体材料描述符领域展开大量的工作，共同推进锂电材料基因组技术的发展和应用。

10.5. 国产相图计算软件的发展

目前而言，国内还未报道国产自主知识产权，并且具有市场竞争力的相图计算软件。大量从事相图计算工作的学者或者研究人员，大多采用的是美国CompuTherm公司的Pandat、瑞典皇家工学院开发的Thermo-Calc以及加拿大的Factsage等计算相图软件。国内有众多的学者从事计算相图工作的研究，或许可以寻找到具体的商业模式和团队展开合作，开发出国产自主知识产权的商业相图计算软件。

10.6. 展望

对锂离子电池中这些基础科学与应用技术问题的理解，对全产业链过程的多尺度计算和模拟，最终有望加速锂离子电池以及下一代锂电池材料的开发过程，帮助我们更快找到高性能、高安全性的正极、负极与电解质材料，促进电池产业的发展。

11. 参考文献