扩散模型：方法与应用综述（Diffusion Models: A Comprehensive Survey of Methods and Applications）

若知乎端阅读体验不佳，可以查看我的语雀文档： 扩散模型：方法与应用综述 · 语雀 (yuque.com)

作者：

LING YANG∗ , Peking University, China

ZHILONG ZHANG∗ , Peking University, China

SHENDA HONG, Peking University, China

RUNSHENG XU, University of California, Los Angeles, USA

YUE ZHAO, Carnegie Mellon University, USA

YINGXIA SHAO, Beijing University of Posts and Telecommunications, China

WENTAO ZHANG, Mila - Québec AI Institute, HEC Montréal, Canada

MING-HSUAN YANG, University of California at Merced, USA

BIN CUI, Peking University, China

封面图来自： https://www. pixiv.net/artworks/8301 9878 。

原论文后面有陆续的修改，最新版可能与本文不全一致。

扩散模型（Diffusion Model）是一类深层生成模型，拥有坚实的理论基础支撑，并且在许多工作中都取得了令人印象深刻的结果。与目前最先进的方法相比，扩散模型已证明了它的成功性，但它通常需要代价高昂的采样程序还有次优的似然估计。目前，人们已在各个方面作出了重大的努力，来改进扩散模型的性能。在本文中，我们对扩散模型的现有变体进行了全面的回顾。具体来说，我们为扩散模型进行了分类，将其分为三种类型：采样加速增强、似然最大化增强和数据泛化增强。我们还介绍了其他生成模型（即变分自编码器、生成对抗网络、归一化流、自回归模型和基于能量的模型），并讨论了扩散模型与这些生成模型之间的联系。然后我们回顾了扩散模型的应用，包括计算机视觉、自然语言处理、波形信号处理、多模态建模、分子图生成、时间序列建模和对抗净化等。此外，我们还提出了与生成模型发展相关的一些新观点。github： https://github.com/YangLing0818/Diffusion-Models-Papers-Survey-Taxonomy 。

CCS Concepts： • 计算方法（Computing methodologies）→ 计算机视觉的任务； 自然语言生成； 机器学习方法。

其他关键词：生成模型、扩散模型、GAN、VAE、基于能量的模型、标准化流、自回归模型、Surve

1.介绍

扩散模型已成为新的最先进的深度生成模型。在图像合成上超越 GAN [45] 之后，扩散模型在众多工作里 [138, 226]都显示出了巨大的潜力，例如计算机视觉 [11, 119, 242]、自然语言处理 [7]、波形信号处理 [26, 110]、多模态建模 [8,176,254]、分子图建模 [3,82,95,116]、时间序列建模 [168] 和对抗性纯化 （adversarial purification）[17]。此外，扩散模型与其他研究领域也有着密切的联系，例如鲁棒学习（robust learning）[101,159,209]、代表性学习（representative learning）[1,132,237,254]和强化学习[92]。然而，原始的扩散模型仍然存在采样过程缓慢的问题，通常需要数千个估计steps才能抽取样本[78]。此外，与基于似然的模型（例如自回归模型 [83]）相比，它也难以与强劲对手对数似然相比。目前人们已经为解决上述各种局限而做出了许多努力，最近的研究也开始从实际角度来提高扩散模型的性能，或者理论角度分析模型容量（model capacity）。

然而，对于算法和应用中扩散模型的这些最新进展，还缺乏一个系统的回顾总结。为了展现这一快速发展的领域的进展，我们对扩散模型进行了全面回顾。我们的工作将阐明扩散模型在设计中的考虑和先进的方法，展示其在不同领域的应用，并指出未来的研究方向。我们在图 1 中提供了这项调查的概要。

扩散概率模型最初受非平衡热力学启发，作为隐变量生成模型（latent variable generative model）而提出的。这类模型可以分为两个过程：首先是前向（forward，或者译为正向）的过程，通过在多个尺度上添加噪声来逐步扰乱数据分布；然后是反向的过程，去学习如何恢复数据结构[78, 186]。从这个角度看，扩散模型可以看作是一个层次很深的VAE(Variational Auto-Encoder)，即上述的破坏和恢复过程分别对应于VAE中的编码和解码过程。

因此，许多研究都集中在对编码和解码过程进行学习，再加上变分下限的设计，来提高模型性能。或者，扩散模型的过程可以看作是随机微分方程 (SDE) [87, 195] 的离散化，其中前向和反向过程对应于前向SDE和反向 SDE。因此，通过 SDE 对扩散模型进行分析，丰富了理论结果，对模型进行了改进，在采样策略方面尤为突出。受这些观点的启发，我们提出：将扩散模型分为三类： 采样加速增强 （第 3 节）、 似然最大化增强 （第 4 节）和 泛化能力增强 （第 5 节）。在每个类别中，我们进一步对模型进行更详细的分析、提出更具体的观点，见图 1。

在分析了这三种扩散模型之后，我们介绍了其他五种常用的生成模型（第 6 节），即变分自编码器、生成对抗网络、归一化流、自回归模型和基于能量的模型。由于扩散模型的良好特性，研究人员开始将传统的生成模型与扩散模型结合使用、进行建模。我们对这些工作也进行了具体介绍，并阐明了扩散模型对原始生成模型的改进。然后我们系统地介绍了扩散模型在广泛任务中的应用（第 7 节），包括计算机视觉、自然语言处理、波形信号处理、多模态建模、分子图生成、时间序列建模和对抗性纯化。对于每个任务，我们对问题做了定义，并介绍了利用扩散模型处理问题的一些工作。在第 8 节中，我们提出了这一快速发展的领域的潜在研究方向，并在第 9 节中进行了总结。

• 新的分类方法 ：我们提出了一种新的系统分类法，用于扩散模型及其应用。 具体来说，我们将现有的扩散模型分为三类：采样加速增强、似然最大化增强和数据泛化增强。此外，我们将扩散模型的应用分为七类：计算机视觉、自然语言处理、波形信号处理、多模态学习、分子图生成、时间序列建模和对抗性纯化。
• 综合回顾 ：我们提供了对现代扩散模型及其应用的综合概述。我们通过详细比较讨论了每种扩散模型主要的改进。对于扩散模型的每种类型的应用，我们都会介绍其设计中的主要问题，并说明它们是如何解决这些问题的。
• 未来研究方向 ：我们为未来研究提供了开放性的问题，并对扩散模型在算法和应用方面的未来发展提出了一些建议。

2.扩散模型的初步研究

生成模型的一个核心问题是：对模型概率分布的灵活性和易处理性之间的权衡。 扩散模型的基本思想是，通过前向扩散过程系统地扰动数据分布中的结构，然后通过学习反向扩散过程来恢复结构，从而产生高度灵活和易于处理的生成模型。 图 2 显示了扩散模型中两种主要范式的比较，即：去噪扩散概率模型和基于得分的生成模型。 表 1 列出了用于描述下述扩散模型的符号。

2.1 去噪扩散概率模型

去噪扩散概率模型 (DDPM) [78] 由两个参数化的马尔可夫链组成，并使用变分推理在有限时间后生成与原始数据匹配的样本。 前向链通过使用预先设计的时间表逐渐添加高斯噪声来扰乱数据分布，直到数据分布收敛到给定的先验，即标准高斯分布。 反向链从给定的先验开始，使用参数化的高斯转换核，学习如何去逐步恢复未受干扰的数据结构。 形式上，给定一个数据分布 \mathbf{x_0}\sim q(\mathbf{x}_0) ，我们定义了一个前向噪声过程 q ，它产生隐变量 \mathbf{x}_1, \mathbf{x}_2,\,...\,,\mathbf{x}_T ，通过在时间 t 添加方差 \beta_t\in (0, 1) 的高斯噪声，如下：

q(\mathbf{x}_1,...,\mathbf{x}_T\vert\mathbf{x}_0) = \prod_{t=1}^Tq(\mathbf{x}_t\vert\mathbf{x}_{t-1})\qquad(1) \\ q(\mathbf{x}_t\vert\mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1-\beta_t}\mathbf{x}_{t-1}, \beta_t\mathbf{I}) \qquad(2)

其中 q(\mathbf{x}_t) 表示隐变量 \mathbf{x}_t 在前向过程中的分布。 如 [78] 中所述，对于一个直接以输入 \mathbf{x}_0 为条件的噪声隐式值，公式(2)中定义的噪声过程允许我们对其任意steps进行采样。

由于 \alpha_t = 1-\beta_t 以及 \bar{\alpha}_t = \prod_{s=0}^ta_s ，我们可以把边际写成：

q(\mathbf{x}_t\vert\mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t}\mathbf{x}_0, (1-\bar{\alpha}_t)\mathbf{I})\qquad(3) \\ \mathbf{x}_t = \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\epsilon\qquad (4)

详细推导可以参考[4, 133]。 当 \bar\alpha_T 接近 0 时， \mathbf{x}_t 实际上与纯高斯噪声无法区分： p(\mathbf{x}_T) \approx \mathcal{N}(\mathbf{x}_T ; 0, \mathbf{I}) 。联合分布 p_\theta(\mathbf{x}_{0:T}) 称为反向过程（或逆过程），当 \beta_t 足够小时， q(\mathbf{x}_{t-1}\vert\mathbf{x}_t) 近似高斯分布。因此，我们可以将这个反向过程参数化如下，从 p(\mathbf{x}_T) = \mathcal{N}(\mathbf{x}_T ; 0, \mathbf{I}) 开始：

p_\theta(\mathbf{x}_{0:T}) = p(\mathbf{x}_T)\prod_{t=1}^Tp_\theta(\mathbf{x}_{t-1}\vert\mathbf{x}_t)\qquad(5)\\ p_\theta(\mathbf{x}_{t-1}\vert\mathbf{x}_t)= \mathcal{N}(\mathbf{x}_{t-1}; \mu_\theta(\mathbf{x}_t\vert t)), \Sigma_\theta(\mathbf{x}_t, t) \qquad (6)

其中 p_\theta(\mathbf{x}_t) 表示隐变量 \mathbf{x}_t 在反向过程中的分布，或简单起见写作 p(\mathbf{x}_t) 。 训练可以通过优化负对数似然的变分上限来完成：

\begin{align}\mathbb{E}[-\log p_\theta(\mathbf{x}_0)] &\leq \mathbb{E}_q\left[-\log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}\right] \qquad(7)\\&= \mathbb{E}_q\left[-\log p(\mathbf{x}_T) - \sum_{t\geq 1}\log \frac{p_\theta(\mathbf{x}_{t-1}\vert\mathbf{x}_t)}{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}\right] \qquad(8)\\&= -L_{VLB} \qquad(9)\end{align}

重新参数化公式（8）[78]，我们有了一个总体目标：

\mathbb{E}_{t\sim\mathcal{U}(0, T), \mathbf{x}\sim q(\mathbf{x}_0), \epsilon\sim\mathcal{N}(0, \mathbf{I})}[\lambda(t)\parallel\epsilon - \epsilon_\theta(\mathbf{x}_t, t)\parallel^2]\qquad (10)

其中 \epsilon_\theta 是一个神经网络，它使用输入 x_t 和 t 来预测可以生成 \mathbf{x}_t 的 \epsilon ，类似于在由 t [191]索引的多个噪声尺度上的去噪分数匹配。 此外， \lambda(t) 是一个正加权函数。 目标函数可以通过蒙特卡洛方法 [146] 进行估计，并使用随机优化器 [196] 进行训练。 在生成过程中，它首先从标准高斯先验中选择一个样本 \mathbf{x}_T ，然后使用学习的反向链顺序绘制样本 \mathbf{x}_t ，直到我们获得新的数据 \mathbf{x}_0 。

2.2 基于得分的生成模型

或者，可以将上述扩散概率模型视为基于得分的生成模型的离散化 [195]。 基于得分的生成模型构建随机微分方程 (SDE) 以将数据分布以平滑的方式扰乱到已知的先验分布，并构建相应的逆时 SDE 以将先验分布转换回数据分布。 形式上，前向扩散过程是以下 SDE 的解：

d\mathbf{x} = \mathbf{f}(\mathbf{x}, t) + g(t)d\mathbf{w} \qquad (11)

其中 \mathbf{w} 是个标准维纳过程，又名标准布朗运动。令 \mathbf{x}_0 为原始数据样本， \mathbf{x}_T 表示近似标准高斯分布的扰动数据。DDPM [78] 中的前向过程可以看作是特殊前向 SDE [195] 的离散化：

d\mathbf{x} = -\frac{1}{2}\beta(t)\mathbf{x}dt + \sqrt{\beta(t)}d\mathbf{w} \qquad (12)

其中 \beta(\frac{i}{N}) = N\beta_i ，当 N 趋于正无穷时就是公式(2)。

要从已知的先验生成数据，可以反转前向扩散 SDE，将 \mathbf{x}_T 转换为 \mathbf{x}_0 。反向 SDE 的解具有与前向 SDE 相同的边际密度，但它在时间上反向演化 [195]。

d\mathbf{x} = \mathbf{f}(\mathbf{x}, t) - g(t)^2\nabla_\mathbf{x}\log q_t(\mathbf{x})dt + g(t)d\bar{\mathbf{w}} \qquad (13)

其中 \bar{\mathbf{w}} 是一个标准的维纳过程，其中时间从 T 倒流到0，而 dt 是一个无穷小的负时间步长。为了逆转扩散过程并生成数据，我们需要的唯一信息是每个时间步长 t 的得分函数： \nabla_\mathbf{x}\log q_t(\mathbf{x}) 。在这里，我们使用 q_t(x) 来表示隐变量 \mathbf{x}_t 在前向过程中的分布。 借用得分匹配[191]的技术，我们可以训练一个基于时间的分数模型 s_\theta(\mathbf{x}_t, t) ，通过优化去噪得分匹配目标来估计得分函数：

\mathbb{E}_{t, \mathbf{x}_0, \mathbf{x}_t}[\lambda_t \parallel s_\theta(\mathbf{x}_t, t) - \nabla_{\mathbf{x}_t}\log q_{0t}(\mathbf{x}_t \vert \mathbf{x}_0)\parallel^2] \qquad (14)

公式(14)中的目标函数与公式(10)密切相关。令 s_\theta(\mathbf{x}_t, t) = -\frac{\epsilon_\theta(\mathbf{x}_t, t)}{\sigma_t} ，并且利用高斯分布的性质，式(14)等价于由加权函数决定的式(10)。因此，可以像在 DDPM 中一样有效地优化方程 (14)。 在具体实现中，需要使用离散化来求解反向 SDE，得到的过程类似于 DDPM 中的反向链。

3.采样加速增强的扩散模型

尽管扩散模型在生成高质量和多样化的样本方面取得了巨大成功，但现有方法通常需要耗时的采样过程，这通常需要对学习的扩散过程进行大量离散化steps才能达到所需的精度。 近年来，人们为加快采样程序做出了重大努力。

3.1离散化优化

在求解扩散 SDE 时，减小离散化步长可以加快采样过程。 然而，这种方法会导致离散化出错，并对模型性能带来负面影响。 因此，人们已经开发了许多方法来优化离散化方案，同时通过求解随机微分方程或常微分方程 (ODE) 来减少采样steps，同时保持良好的样本质量 [33,96,126,129,195,245]。

3.1.1 SDE 求解器

已经有许多方法来解决连续时间设置中的反向扩散 SDE。 SGM [195] 旨在以与前向 SDE 相同的方式离散化反向时间 SDE。 将前向 SDE 和反向 SDE 离散化为方程 (11) 和方程 (13)，并假设以下迭代规则是前向 SDE 的离散化：

\mathbf{x}_{i+1} = \mathbf{x}_i + \mathbf{f}_i(\mathbf{x}_i)+\mathbf{g}_i\mathbf{z}_i, i = 0,1,...,N-1 \qquad(15)

其中 z_i \sim \mathcal{N}(0, \mathbf{I}) ， \mathbf{f}_i 和 \mathbf{g}_i 由 SDE 和离散化方案确定。 可以用经过训练的得分函数 s_{\theta^*}(x_i, i)) 离散化逆时间的SDE：

\mathbf{x}_i = \mathbf{x}_{i+1} - \mathbf{f}_{i+1}(\mathbf{x}_{i+1}) + \mathbf{g}_{i+1}\mathbf{g}^t_{i+1}s_{\theta^*}(\mathbf{x}_{i+1}, i+1) + \mathbf{g}_{i+1}\mathbf{z} \qquad(16)

该过程可以应用于任何扩散模型，经验结果表明，该采样器的性能略好于 DDPM [195]。 此外，SGM 提出在 SDE 求解器（solver）中添加一个“校正器（corrector）”，以生成具有正确边际分布的样本。 具体来说，在数值 SDE 求解器在每个时间step都对样本进行估计后，“校正器”将使用马尔可夫链蒙特卡罗方法校正估计样本的边际分布。 实验结果表明，添加校正器比使用更多的steps更有效 [195]。

另一方面，一种自适应步长 SDE 求解器将快速高阶 SDE 求解器与由 Jolicoeur-Martineau 等人开发的精确低阶 SDE 求解器相结合。 [96] 在每个时间steps，高阶和低阶求解器从先前的样本 \mathbf{x}'_{prev} 生成新的样本 \mathbf{x}'_{high} 和 \mathbf{x}'_{low} 。 如果 \mathbf{x}'_{high} 和 \mathbf{x}'_{low} 相似，算法会接受 \mathbf{x}' 作为在当前步对 \mathbf{x}'_{high} 和 \mathbf{x}'_{low} 进行插值得到的新样本，并增加步长 。\mathbf{x}'_{high} 和 \mathbf{x}'_{low} 之间的不一致性（dissimilarity）定义为：

E_q = \left\Vert \frac{\mathbf{x}'_{low} - \mathbf{x}'_{high}}{\delta(\mathbf{x}, \mathbf{x}'_{prev})} \right\Vert^2 \qquad(17)

其中 \delta(\mathbf{x}'_{low}, \mathbf{x}'_{high}) = \max (\epsilon_{abs}, \epsilon_{rel} \max (\vert \mathbf{x}'\vert, \vert\mathbf{x}'_{prev}\vert)) 是公差（tolerance），且 \epsilon_{abs} 和 \epsilon_{rel} 是超参数。如果 E_q \leq 1 ，那么 \mathbf{x}'_{high} 与 \mathbf{x}'_{low} 相近，结果是比较准确的。因此，可以将外推样本（extrapolation sample）用作该时间step的新样本，因为它可以被视为以大步长绘制的准确样本。

受 SDE 收缩理论的启发，CCDF [33] 表明，从具有更好初始化的单个前向扩散出发，可以显著减少采样steps的数量。 在每个生成steps中，每个样本都通过非扩展线性映射进行转换：

\widetilde{\mathbf{x}}_{i-1} = f(\mathbf{x}_i, i) + g(\mathbf{x}_i, i)\mathbf{z}_i \qquad(18)\\\mathbf{x}_{i-1} = \mathbf{A\widetilde{x}}_{i-1} + \mathbf{b} \qquad (19)

其中 \mathbf{z}_i\sim\mathcal{N}(0,\mathbf{I}) ，且 \mathbf{A} 是非扩展的：

\Vert\mathbf{Ax - Ay}\Vert\leq\mathbf{x-y},\quad \forall \mathbf{x, y} \qquad(20)

使用随机收缩理论，可以证明：存在一条等待A的较短采样路径，并且该较短采样路径的估计误差受原始估计误差的限制。 因此，我们可以在更早的step开始生成，以获得更好的结果。 最近，DSB [42] 通过将逆过程学习视为薛定谔桥（Schrödinger Bridge）问题来扩展 SGM。它提出了使用迭代比例拟合过程的近似来解决具有一定离散化的SB问题。 此外，DSB 提供了生成建模和最优运输问题（optimal transport problem）之间的联系。

3.1.2 ODE 求解器

ODE求解器不需要高斯采样作为SDE求解器的过程，因此可以提高扩散模型的采样效率。 如 SGM [195] 所示，每个扩散模型都有一个对应的 ODE，其边缘分布与扩散 SDE 相同：

d\mathbf{x} = \mathbf{f}(\mathbf{x}, t) - \frac{1}{2}g(t)^2\nabla_{\mathbf{x}}\log q_t(\mathbf{x})dt \qquad(21)

因此我们可以设计更好的 ODE 求解器，并使用派生的离散化 ODE [99, 126, 129, 245] 生成数据。 DPM求解器 [129] 演示了扩散 ODE 解的精确公式。 该公式解析计算该解的线性部分，而非线性部分可以通过神经网络的指数加权积分来近似。 形式上，它将以下包含 DDPM 的扩散 ODE 视为特例：

\frac{d\mathbf{x}_t}{dt} = f(t)\mathbf{x}_t -\frac{1}{2} g^2(t)\nabla_{\mathbf{x}}\log q_t(\mathbf{x}_t) \qquad(22) \\\mathbf{x}_t = e^{\int_s^tf(\tau)d\tau}\mathbf{x}_s + \int_{s}^t\left(e^{e^{\int_\tau^t}f(r)dr}\frac{g^2(\tau)}{2\sigma_\tau}\epsilon_\theta(\mathbf{x}_\tau, \tau)\right)d\tau \qquad (23)

其中学习的得分函数 -\frac{\epsilon_\theta(\mathbf{x}_\tau, \tau)}{\sigma_\tau} 用于替换 oracle 得分函数。 该公式可以减少线性部分的离散化误差，从而可以在保持样本质量的同时减少采样步数。 此外，它可以通过将分数函数扩展到高阶来减少拟合误差，这种方法在理论上是有保证的。 它进一步提出了结合不同阶数的求解器来动态调整步长以提高效率，如[96]。

DEIS [245] 还利用了学习扩散过程的半线性结构，并为方程（23）得出了类似的解。 该方法提出使用二次时间步长离散化扩散 ODE，如 DDIM [188]。 它还提出使用指数积分器来近似计算 ODE 在时间步中的解，并使用多项式外推法来进行更好的分数估计。 在估计时间离散化 \{t_i\}_{i=0}^N 时的得分函数 \epsilon_\theta(x_{t_i}, t_i) 后，它拟合了关于插值点 (t_i, \epsilon_\theta(\mathbf{x}_{t_i}, t_i)) 的r次多项式 \mathbf{P}_r(t) ：

\mathbf{P}_r(t) = \sum_{j=0}^{r}\left[\prod_{k\neq j} \frac{t - t_{i+k}}{t_{i+j}-t_{i+k}}\right]\epsilon_\theta(\mathbf{x}_{t_{i+j}}, t_{i+j}) \qquad(24)

然后它使用 \mathbf{P}_r(t) 在区间 [t_{i−1}, t_i] 上逼近 \epsilon_\theta(x_\tau , \tau) 。 结合所有成分可以减少离散化和拟合误差，从而减少了估计steps。 PNDM [126] 证明我们可以通过求解流形上的 DDPM 微分方程来设计更快的高阶 ODE。 [99] 说明了解决方案轨迹的切线应该指向去噪输出，通过适当设计噪声调度来减少离散化误差。

3.2 非马尔可夫过程

马尔可夫过程只依赖于最后一步的样本进行预测，限制了对先前丰富的样本信息进行利用。 相比之下，非马尔可夫过程的转换核可以依赖更多的样本，并且可以利用来自这些样本的更多信息。 因此，它可以以较大的步长进行准确的预测，从而相应地加快了采样过程。 DDIM [188] 将原始的 DDPM 扩展到非马尔可夫情况。 形式上，DDIM 提出前向扩散链为：

q(\mathbf{\mathbf{x}_1}, ..., \mathbf{x}_T \vert \mathbf{x}_0) = \prod_{t=1}^Tq(\mathbf{x}_t\vert\mathbf{x}_{t-1}, \mathbf{x}_0) \qquad (25)\\q_\sigma(\mathbf{x}_{t-1}\vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}\vert\widetilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0), \sigma_t^2\mathbf{I}) \qquad (26) \\\widetilde{\mu}_t(\mathbf{x}_t\vert\mathbf{x}_0) = \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0 + \sqrt{\bar{\beta}_{n-1}-\sigma_t^2} \cdot \frac{\mathbf{x}_n - \sqrt{\bar{\alpha}_t}\mathbf{x}_0}{\sqrt{\bar{\beta}_t}} \qquad(27)

该公式将 DDPM 和 DDIM 封装为特殊情况。 此外，DDIM 的生成方案可以看作是 ODE 的特殊离散化； 因此，可以确定性地对数据进行采样。 gDDIM [246] 对 DDIM [188] 的优势提供了深刻的解释，并提出了一种将 DDIM 扩展到通用扩散模型的算法，如 CLD [49]。 PNDM [126] 证明了 DDPM 应该被视为在流形上求解微分方程，并提出了一种具有快速采样速度的伪数值求解器。 他们的方法也将 DDIM 封装为一个特例。 GGDM [213] 提出在生成过程的每个步骤中使用所有先前的样本来预测下一个样本，这对 DDIM 进行了推广。 它还利用 DDSS [213] 通过区分样本质量分数在几个时间steps内优化快速采样器。

3.2 部分取样

或者，可以通过仅使用反向过程中的部分steps来生成样本，以样本质量换取采样速度。 [213] 建议使用动态规划算法选择一个最优子轨迹，使训练的 VLB 最大化。 那么这个子轨迹只能用一代。 这里关键的一点是，我们可以根据子轨迹分解 VLB。 给定推理时间steps 0 \leq t'_0 \leq t'_1 \leq ... \leq t'_{K-1} \leq t'_K = T 的路径，可以得出相应的 ELBO：

-L_{VLB} = \mathbf{E}_q\mathbf{D}_{KL}[q(x_1\vert x_0) \Vert p_\theta(\mathbf{x}_1)]+\sum_{i=1}^K L(t_i', t_{i-1}') \qquad (28) \\L(t, s)= \left\{\begin{aligned}-\mathbf{E}_q \log p_\theta(\mathbf{x}_t\vert \mathbf{x}_0) \qquad s = 0 \\ \mathbf{E}_q\mathbf{D}_{KL}q(\mathbf{x}_s\vert \mathbf{x}_t, \mathbf{x}_0)p_\theta(\mathbf{x}_s\vert\mathbf{x}_t) \qquad s > 0\end{aligned} \qquad (29)\right.

因此，每个 L(i，j) 都会被记住，并且可以应用动态规划，为所有预训练的 DDPM 选择具有连续时间steps的最优轨迹。 结合 Analytic-DPM 中的结果，确实可以选择最优的子轨迹。

或者，可以通过提前停止或截断正向和反向过程来实现部分采样[141、251]，或者通过知识蒸馏来重新训练学生网络并跳过部分steps[131、178]。 在 Progressive Distillation [178] 中，它提出从预训练的扩散模型中提炼出新的扩散模型，而新的扩散模型只使用了预训练扩散模型中一半的采样steps。 具体来说，给定一个训练有素的教师扩散模型，学生扩散模型的训练方式是学生模型中的一个step匹配教师模型中的两个steps。 然后它逐步将此“蒸馏”过程应用于学生扩散模型，以进一步减少采样步骤。

4.具有似然最大化增强的扩散模型

与其他基于似然的模型 [78, 106] 相比，去噪扩散概率模型 (DDPM) [78] 中最有竞争力的是对数似然，并且最近有各种方法可以增强对数似然的最大化。 由于直接计算对数似然的难处理性，研究主要集中在设计和分析变分下界。 优化 VLB 的方法有三种：噪声调度优化、可学习反向方差和目标设计。 在下文中，我们将详细讨论它们。

4.1 噪声调度优化

在离散时间的条件中，我们可以通过调整前向过程中的噪声调度来优化 VLB [106, 149]。 在 [149] 中，人为制造的噪声调度和反向方差估计已经实现了具有竞争力的对数似然。 它提出了以下噪音调度（noise schedule）：

\bar{\alpha}_t = \frac{h(t)}{h(0)}, \quad h(t) = \cos \left(\frac{t/T + m}{1+m} \cdot \frac{\pi}{2}\right) \qquad (30)

其中 \bar{\alpha}_t 在公式(4)中定义。 可以使用 \beta_t = 1 - \frac{\bar{\alpha}_t}{\bar{\alpha}_t - 1} 来计算公式 (2) 中的前向方差。 在这个方案中， \bar{\alpha}_t 平滑变化，且防止了噪声水平的突然变化。 因此，反向过程可以很容易地恢复数据结构。

VDM [106] 表明，数据 \mathbf{x} 的变分下限可以通过扩散数据的信噪比的 \mathrm{R}(t) = \frac{\alpha^2(t)}{\sigma^2(t)} 简化成一个简短的表达式：

\begin{align} \mathcal{L}(\mathbf{x}_0) &= \frac{T}{2}\mathbb{E}_{\epsilon ,t}\left[\left(\mathrm{R}\left(\frac{t-1}{T}\right)-\mathrm{R}\left(\frac{t}{T}\right)\right)\Vert\mathbf{x}_0 - \hat{\mathbf{x}}_\theta(\mathbf{x}_t;t)\Vert_2^2\right] \qquad(31) \\ &\approx -\frac{1}{2}\mathbb{E}_\epsilon\int_0^1\mathrm{R}'(t)\Vert \mathbf{x}_0-\hat{\mathbf{x}}_\theta(\mathbf{x}_t;t)\Vert_2^2\quad \text{as}\;\;T \rightarrow \infty \qquad(32)\\ &= -\frac{1}{2}\mathbb{E}_{\epsilon,t\sim\mathcal{U}(0,1)}[\mathrm{R}'(t)\vert\mathbf{x}_0 - \hat{\mathbf{x}}_\theta(\mathbf{x}_t;t)\vert^2_2] \qquad(33) \end{align}

其中， \mathbf{x}_t 表示经过 t 个steps后损坏的数据（corrupted data） \mathbf{x} ， \mathbf{x}_t = \alpha(t)\mathbf{x}_0 +\sigma^2(t)\epsilon 。 将变量变化公式应用于公式(32)中的目标函数表明，在无限深的条件下，VLB 完全由噪声调度的终点决定：

\mathcal{L}(\mathbf{x}) = \frac{1}{2}\mathbb{E}_{\epsilon\sim \mathcal{N}(0, \mathbf{I})}\int_{\mathrm{R_{min}}}^{\mathrm{R_{max}}}\Vert\mathbf{x}-\widetilde{\mathbf{x}}_\theta(\mathbf{x}_v, v)\Vert_2^2dv \qquad (34)

因此，在无限深的设置条件下，端点之间的噪声调度不会影响VLB。可以交替优化端点之间的噪声调度以减少方差，并优化VLB端点。

4.2 可学习反向方差

或者，优化反向方差估计，从而减少拟合误差，可以有效地最大化VLB和对数似然。[149]观察到，在逆向过程中学习方差可以减少数量级的采样步骤。它人为地将方程（6）中的反向方差设置为：

\Sigma_\theta(\mathbf{x}_t, t) = \exp(v\cdot \log \beta_t + (1-v)\cdot\log \widetilde{\beta}_t)\qquad (35)

其中 \widetilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} 。 \beta_t 和 v 是使用VLB学习的参数。 这种简单的调整可以减少采样的时间步长。Analytic-DPM [10] 证明了一个令人瞩目的结果，即： 即VLB的最优反向方差DDPM具有与其得分函数相关的分析形式：

\Sigma_\theta(\mathbf{x}_t, t) = \sigma_t^2 + \left(\sqrt{\frac{\bar{\beta}_t}{\alpha_t} } -\sqrt{\bar{\beta}_{t-1} - \sigma_t^2}\right)^2 \cdot \left(1 - \bar{\beta}_t\mathbb{E}_{q_t(\mathbf{x}_t)}\frac{\Vert\nabla_{\mathbf{x}_t}\log q_t(\mathbf{x}_t)\Vert^2}{d}\right) \qquad (36)

因此，在准确估计得分函数的情况下，可以实现最优逆向过程，从而实现最优 VLB。

4.3 目标设计

利用扩散 SDE，可以得出生成数据的对数似然与分数匹配目标之间的联系。 通过适当地设计目标，可以最大化 VLB 和对数似然。 在连续时间的设置条件下，新数据由具有学习得分函数 s_\theta(\mathbf{x}_t, t) 的插入反向 SDE（ plug-in reverse SDE ）生成：

d\mathbf{x} = f(\mathbf{x}, t) - g^2(t)s_\theta(\mathbf{x}_t, t)dt + g(t)d\mathbf{w} \qquad(37)

此外，数据可以由学习的扩散 ODE 生成：

\frac{d\mathbf{x}_t}{dt} = f(t, \mathbf{x}_t) - \frac{1}{2}g^2(t)s_\theta(\mathbf{x}_t, t) \qquad (38)

研究集中在最大化上述 SDE 和 ODE 在时间 0 的解的可能性，分别表示为 p_0^{sde} 和 p_0^{ode} [87, 128, 190]。 [190]证明，使用特定的加权方案，目标可以是生成样本的负对数似然的上限； 因此，它可以对基于得分的扩散模型进行近似最大似然训练：

\mathbf{D}_{KL}(q_0 \Vert p_0^{sde}) \leq \mathcal{L}(\theta; g(\cdot)^2) + \mathbf{D}_{KL}(q_T\Vert \pi) \qquad (39)

其中， \mathcal{L}(\theta; g(\cdot)^2) 是等式 (14) 中的目标，权重函数为 \lambda(t) = g(t)^2 。 由于 \mathbf{D}_{KL}(q_0 \Vert p_0^{sde}) = -\mathbb{E}_{q_0}\log (p_0^{sde}) + C ，所提出的加权方案可以限制生成样本的负对数似然。同时，[87] 和 [190] 都证明了任何给定样本的负对数似然可以限制如下：

-\log p_0^{sde} (\mathbf{x}) \leq \mathcal{L}'(\mathbf{x}) \qquad (40)

\mathcal{L}'(\mathbf{x}) 定义如下：

\int_0^T\mathbb{E}\left[\left.\frac{1}{2}\Vert g(s)s_\theta(\mathbf{x}_s, s)\Vert^2 + \nabla\cdot (g(s)^2 - f(s, \mathbf{x}_s))\right|\mathbf{x}_0 = \mathbf{x}\right]ds - \mathbb{E}_{\mathbf{x}_T}\left[\log p_0^{sde}\right(\mathbf{x}_T) \vert \mathbf{x}_0 = \mathbf{x}]

公式(41)的第一部分（注：原文似乎弄混了公式标号）可以看作是隐式分数匹配方法的目标[89]。 因此，匹配得分函数相当于最小化由插入反向SDE 生成的样本负对数似然的上限。

另一方面，[128] 证明我们需要限制一阶、二阶和三阶分数匹配误差，以最大化学习扩散 ODE 的似然性。 它表明，匹配一阶分数不足以最大化扩散 ODE 中生成数据的对数似然：

\mathbf{D}_{KL}(q_0\Vert p_0^{ode}) = \mathbf{D}_{KL}(q_T\Vert p_T^{ode}) + \mathcal{L}_{ode}(\theta) \qquad (41)

其中， \mathcal{L}_{ode}(\theta) = \mathcal{L}(\theta, g(\cdot)^2) + \mathcal{L}_{dif}(\theta) ，且：

\mathcal{L}_{dif}(\theta) := \frac{1}{2}\int_0^Tg(t)^2\mathbb{E}_{q_t(\mathbf{x}_t)}\left[(s_\theta(\mathbf{x}_t, t) - \nabla_{\mathbf{x}}\log q_t(\mathbf{x}_t))^\top(\nabla_{\mathbf{x}}\log p_t^{ode}(\mathbf{x}_t)-s_\theta(\mathbf{x}_t, t))\right]dt \;\; (42)

因此，单独优化 \mathcal{L}(\theta; g(\cdot)^2) 并不等同于最小化概率流 ODE 中样本似然的上限。 此外，可以证明，在温和的条件下，可以通过匹配得分函数的一阶、二阶和三阶来最小化似然的上限。 此外，目前也有行之有效的训练算法。 SB-FBSDE [27] 使用随机最优控制技术，为薛定谔桥 (SB) 模型的似然训练提供了一种新颖的计算框架。 它为 SB 模型构建了新的似然目标，并将 SGM 的似然目标封装为特例 [87, 190]。

5.具有数据泛化增强的扩散模型

扩散模型假设数据支持欧几里得空间，即具有平面几何形状的流形。 而添加高斯噪声将不可避免地将数据转换为连续的状态空间。 各种研究都集中在解决这些限制上 [7, 19, 41, 71, 86, 126, 153, 204, 215, 225]。 数据泛化有两种方法：特征空间统一（Feature Space Unification）和 数据依赖的转换核（Data-Dependent Transition Kernels），我们将详细讨论它们。

5.1 特征空间统一

要将扩散模型应用于任何数据类型，可以通过首先将数据编码到连续隐空间然后将扩散模型应用于空间来统一特征空间，这依赖于 VAE 框架。 这里的关键问题是如何设计损失函数来联合学习 VAE 和扩散模型，因为隐变量的先验分布应该同时实现灵活性和易处理性。 LSGM [204] 直接处理连续时间设置中的问题。 它确定，由于隐式先验的难处理性，分数匹配损失不再适用：

\nabla_{\mathbf{x}}\log p_t(\mathbf{x}) = \int \log q_{0t}(\mathbf{x}_t\vert\mathbf{x}_0)p_\theta(\mathbf{x}_0)d\mathbf{z} \qquad(43)

其中 p_\theta(\mathbf{x}_0) 是由神经网络参数化的隐式先验。 对于基于得分的生成模型中的目标来说，这个问题是不可避免的，因为它们需要前向过程中的得分函数可用或加前缀。 使用 VAE 中的 ELBO 作为损失函数，LSGM [204] 将 ELBO 与基于得分的生成模型中的得分匹配目标联系起来，从而实现高效的训练和采样。已被证明，ELBO中的交叉熵项 \mathcal{H}(q(\mathbf{x}_0 |\mathbf{x}), p(\mathbf{x}_0)) 可以转化为：

\mathbb{E}_t\left[\frac{g(t)^2}{2}\mathbb{E}_{q_{0t}(\mathbf{x}_t, \mathbf{x}_0\vert\mathbf{x})}\left[\Vert\nabla_{\mathbf{x}_t}\log q(\mathbf{x}_t\vert \mathbf{x}_0) - \nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t)\Vert_2^2\right]\right] \qquad (44)

其中 q(\mathbf{x}_0\vert \mathbf{x}) 和 p(\mathbf{x}_0) 是SDE 的边际分布（方程（11））， \mathbf{x} 是原始数据， t\sim \mathcal{U}[0, 1] 。 使用这个公式和 \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t |\mathbf{x}_0) ，事实上是易于处理的，可以参数化 \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t) 并优化 ELBO。 [215]使用了另一种方法并通过设计扩散模型的VLB结合VAE的重建损失来规避该问题。

或者，可以采取统一的观点，即特征空间是一个流形。 最近的研究已经将扩散模型推广到流形中的数据，包括作为特例的图 [86, 126, 203]。 假设温和的条件适合一大类流形，例如球体和环面，RSGM [19] 证明我们可以扩展流形上的扩散模型，而 PNDM [126] 提出了一种伪数值方法来求解流形上的微分方程。

5.2 数据依赖的转换核

还可以通过设计适合数据类型的转换核来直接扩散数据。 VQ-Diffusion 和 D3PM [7, 71, 225] 将 DDPM 推广到离散状态情况，其中数据是二进制或者分类的。 这里的噪声是对所有状态的随机游走或随机掩码操作。 转换核可以写成如下的样子：

q(\mathbf{x}_t\vert\mathbf{x}_{t-1}) = \mathbf{v}^\top(\mathbf{x}_t)\mathbf{Q}_t\mathbf{v}(\mathbf{x}_{t-1}) \qquad(45)

其中 \mathbf{v(x)} 是独热码（one-hot）列向量， \mathbf{Q}_t 是惰性随机游走的转换核。其他方法包括使用吸收状态核或离散高斯核[7]。[21]为离散数据的去噪扩散模型提供了连续时间框架，并推导出了新的转换核和采样器。 这里未解决的问题是：离散空间中的数据没有得分函数，即使在连续时间设置中也是如此。 如需进一步讨论，请参阅第 8 节。

还有其他数据结构的泛化示例，例如图形和点云[153, 228]。为了获得有序不变的图分布，EDP-GNN [153] 设计了一个等变置换（permutation-equivariant）图神经网络，通过添加对称噪声来对数据分布的梯度进行建模。 为了生成在旋转和平移下不改变的点云数据分布，GEODIFF [228] 证明了，从不变先验开始并随着等变马尔可夫核演化的马尔可夫链可以产生不变的边际分布。 形式上， \mathcal{T} 是旋转或平移操作，如果：

p(\mathbf{x}_T) = p(\mathcal{T}(\mathbf{x}_T)), \quad p(\mathbf{x}_{t-1}\vert\mathbf{x}_t) = p(\mathcal{T}(\mathbf{x}_{t-1})\vert \mathcal{T}(\mathbf{x}_t)) \qquad(46)

那么边际分布是不变的，即 p_0(\mathbf{x}) = p_0(\mathcal{T}(\mathbf{x})) 。他们进一步为等变马尔可夫核构建了blocks。

6.与其他生成模型的联系

生成模型是一个有很多种应用的热门研究领域。 例如，它们可用于生成高质量图像 [100]、合成逼真的语音和音乐 [205]、推进半监督学习 [38、108]、识别对抗性示例 [193]、进行模仿学习 [77] ，并在强化学习中进行优化[156]。 在每个小节中，我们首先介绍其他五类重要的生成模型，并分析它们的优点和局限性。 然后我们介绍了扩散模型是如何与它们联系起来的，并说明了这些生成模型是如何通过结合扩散模型来提升的。 将扩散模型与其他生成模型集成的算法总结在表 3 中，我们还在图 3 中提供了示意图。

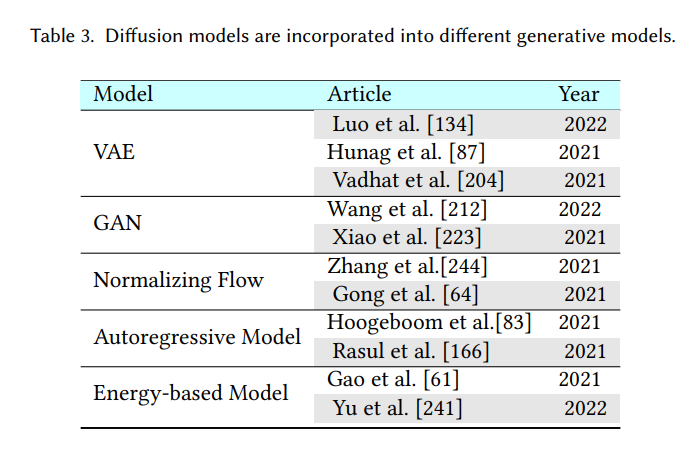
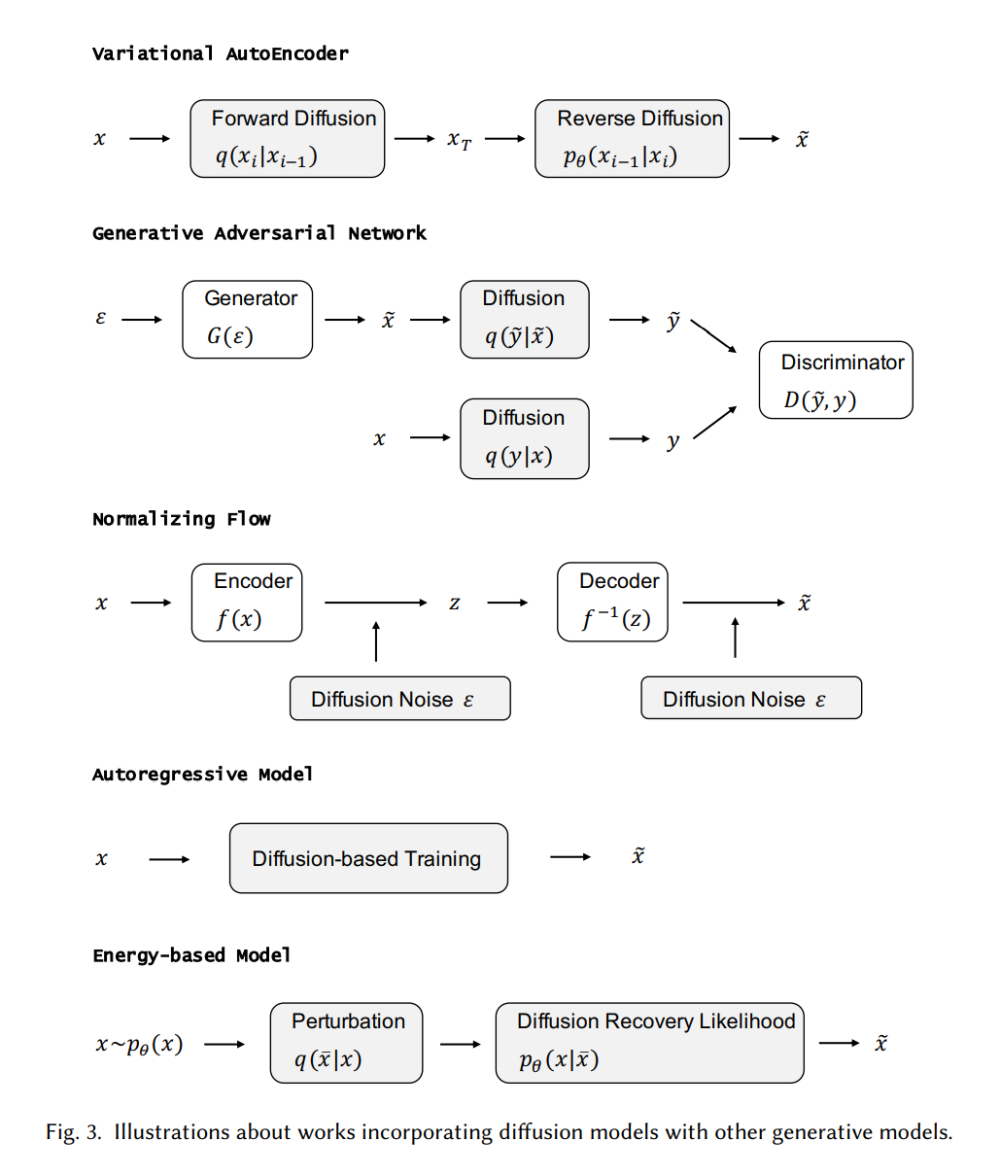
6.1 变分自编码器及其与扩散模型的联系

变分自动编码器 [50, 109, 171] 期望同时学习编码器和解码器，以将输入数据映射到连续隐空间中的值。 它们提供了一个公式，其中嵌入（embedding）可以解释为概率生成模型中的隐变量，概率解码器可以通过参数化似然函数来公式化。 该模型假设数据 \mathbf{x} 是由一些未观察到的隐变量 \mathbf{z} 使用条件分布 p_\theta(\mathbf{x}|\mathbf{z}) 生成的，并且它使用 q_\phi(\mathbf{z}|\mathbf{x}) 来近似推断 \mathbf{z} 。 为了保证推理有效，一种变分贝叶斯方法和这个过程是通过最大化证据下限（ELBO）来实现的：

\mathcal{L}(\phi, \theta; \mathbf{x}) = \mathbb{E}_{q(\mathbf{z}\vert \mathbf{x})}[\log p_\theta(\mathbf{x}, \mathbf{z}) - \log q_\phi(\mathbf{x} \vert \mathbf{z})] \qquad (47)

其中 \mathcal{L}(\phi, \theta; \mathbf{x}) \leq \log p_\theta(x) 。假设参数化似然函数 p_\theta (\mathbf{x}|\mathbf{z}) 和参数化后验近似值 q_\phi(\mathbf{z}|\mathbf{x}) 可以逐点计算，并且可以通过它们的参数进行微分，则可以通过梯度下降来最大化 ELBO。 它允许灵活选择编码器和解码器模型。 通常，它们将由指数族分布表示，其参数由多层神经网络生成。

DDPM 可以被视为分层马尔可夫 VAE 并带有前缀编码器。 前向过程表示编码器，反向过程表示解码器。 此外，DDPM 跨多个层共享解码器，并且所有隐变量与样本数据的大小相同 [134]。 在连续时间设置中，[87] 证明了分数匹配目标可以通过深度分层 VAE 的 ELBO 进一步近似。 通过这种方式，优化扩散模型可以被视为训练一个无限的、深度的、分层的 VAE，这证明了扩散模型可以被解释为分层 VAE 的连续限制的普遍信念。 [204]还通过扩散隐空间来说明ELBO是一个特殊的分数匹配目标。

6.2 生成对抗网络及其与扩散模型的联系

生成对抗网络 (GAN) [36, 65, 72] 因其有趣的对抗思想和十分有前途的架构而受到了广泛关注。 GAN 主要由两个模型组成：生成器 和鉴别器 。 这两个模型通常由神经网络构建，但可以以任何形式的可微系统实现，该系统将输入数据从一个空间映射到另一个空间。 生成器 尝试对真实示例的分布进行建模，并生成新的示例。 鉴别器 通常是一个二元分类器，用于以最大可能的准确度从真实示例中识别生成的示例。GAN 的优化可以看作是一个minimax优化问题，其价值函数 ( , ) 如下：

\min_G\max_D\mathbb{E}_{x\sim p_{\mathrm{data}}(x)}[\log D(\mathbf{x})] + \mathbb{E}_{\mathbf{z}\sim p_z(\mathbf{x})}[\log(1-D(G(\mathbf{z})))] \qquad (48)

优化在鞍点（saddle point）处结束，该鞍点产生关于生成器的最小值和关于判别器的最大值。 这意味着GAN优化的目标是实现纳什平衡（Nash equilibrium）[169]。 此时，可以认为生成器已经捕获了真实示例的准确分布。

GAN 的主要实际问题之一是训练过程中的不稳定性，这主要是由于输入数据的分布与生成数据的分布不重叠造成的。 一个实用的解决方案是将噪声作为鉴别器的输入。 利用灵活的扩散模型，[212] 提出使用由扩散模型确定的自适应噪声调度向鉴别器注入噪声。 相反，GAN 可以帮助提高扩散模型的采样速度。 [223] 认为慢采样是由去噪step中的高斯假设引起的，这仅适用于小步长。 因此，它建议使用条件 GAN 对每个去噪step进行建模，从而允许更大的步长。

6.3 归一化流及其与扩散模型的联系

因其精确的密度评估和对高维数据建模的能力 [48, 107]，归一化流（Normalizing flows）[47, 170] 是一类很有前途的模型。 归一化流可以将简单的概率分布转化为极其复杂的概率分布，可用于生成模型、强化学习、变分推理等领域。 构建它所需的工具是行列式、雅可比矩阵和随机变量的变量替换定理（Change of Variable Theorem）。 归一化流的轨迹由微分方程表示。 在离散时间设置中，归一化流中从数据 \mathbf{x} 到隐式 \mathbf{z} 的映射是一系列双射函数的组合，如 = _ \circ _{ -1} \circ ... \circ _1 。对所有 i \leq N 轨迹 \{\mathbf{x}_1, \mathbf{x}_2, . . .,\mathbf{x}_ \} 都满足：

\mathbf{x}_i = F_i(\mathbf{x}_{i-1}, \theta), \quad \mathbf{x}_{i-1} = F_i^{-1}(\mathbf{x}_i, \theta) \qquad (49)

与连续条件类似，在基于随机变量的变量替换定理的规范化流中可以访问精确的对数似然。 不幸的是，无论是在经验上还是理论上来说 [35, 216]，对双射的要求都导致了对复杂数据的建模的局限性。一些工作试图放宽双射的要求 [48, 216]。DiffFlow[244] 提出了一种新颖的生成建模算法，结合了基于流的模型和扩散模型的优点。

因此，它不仅可以获得比归一化流更清晰的边界，还可以通过比扩散概率模型更少的离散化步骤来学习更一般的分布。

6.4 自回归模型及其与扩散模型的联系

自回归模型 (ARM) 是使用概率链规则，将数据的联合分布分解为条件分布的乘积：

\log p(\mathbf{x}_{1:T}) = \sum_{t=1}^T\log p(\mathbf{x}_t\vert\mathbf{x}_{<t}) \qquad (50)

其中 \mathbf{x}_{<t} 是 \mathbf{x}_1, \mathbf{x}_2,..., \mathbf{x}_{t-1} 的简写[13, 113]。深度学习的最新技术在各种模式上都取得了巨大的进步，例如图像 [30、206]、音频 [98、205] 和文本 [14、20、69、144、145]，它们被称为语言文本建模中的模型。可以通过调用单个神经网络来检索ARM的可能性；从模型生成样本需要与数据维度相同数量的网络调用。尽管自回归模型是一个非常强大的密度估计器，但采样本质上也是一个连续过程，并且在高维数据上可能会非常慢。自回归扩散模型 (ARDM) [83] 提出了一种不同的自回归模型，它学习生成任意顺序的数据。 ARDM 扩展了与顺序无关的自回归模型和离散扩散模型 [7, 84, 187]。与 ARM 不同，ARDM 不需要对表示进行因果屏蔽，因此可以以有效的目标进行训练，这类似于扩散概率模型。在测试过程中，ARDM 能够并行地生成，因此它可以应用于任意预算生成任务。

6.5 基于能量的模型及其与扩散模型的联系

基于能量的模型 (EBM) [23, 44, 52, 56, 59, 60, 66-68, 105, 112, 115, 147, 152, 161, 172, 224, 249] 最近受到了很多关注。 EBM 可以看作是鉴别器的一种生成版本 [68, 93, 114, 117]，同时可以从未标记的输入数据中学习。 令 \mathbf{x}\sim p_{data}(\mathbf{x}) 表示训练样本， p_\theta(\mathbf{x}) 表示一个旨在逼近 p_{data}(\mathbf{x}) 模型的概率密度函数。 基于能量的模型 (EBM) 定义如下：

p_\theta(\mathbf{x}) = \frac{1}{Z_\theta}\exp(f_\theta(\mathbf{x})) \qquad(51)

其中 Z_\theta = \int \exp(f_\theta(\mathbf{x}))d \mathbf{x} 是划分函数。对于高维 \mathbf{x} ，在分析上是难以处理的。 对于图像， f_\theta(\mathbf{x}) 由具有标量输出（scalar output）的卷积神经网络参数化。

尽管 EBM 具有许多理想的特性，但在高维数据上训练 EBM 仍然存在两个挑战。首先，通过最大化似然性来学习 EBM 需要马尔可夫链蒙特卡罗 (MCMC) 方法从模型中生成样本，这可能非常昂贵。其次，如 [151] 中所证明的，使用非收敛 MCMC 学习的能量势（energy potentials）不稳定，因为来自长期马尔可夫链的样本可能与观察到的样本有显着差异，因此很难评估学习的能量势。最近的一项研究 [61] 提出了一种扩散恢复似然方法，可以在扩散模型的逆过程中从一系列 EBM 中轻松学习样本。每个 EBM 都经过恢复似然训练，旨在最大化数据在特定噪声水平下的条件概率，因为它们的噪声版本处于较高的噪声水平。 EBM 最大化恢复似然，因为它比边际似然更容易处理，因为从条件分布中抽样比从边际分布中抽样容易得多。该模型可以生成高质量的样本，并且来自条件分布的长期 MCMC 样本仍然类似于真实图像。

7.扩散模型的应用

扩散模型由于其灵活性和强度，最近已有了许多实际应用。 在本节中，我们将这些应用分为七个部分，包括计算机视觉、自然语言处理、波形信号处理、多模态学习、分子图建模、时间序列建模和对抗性纯化。 在每个小节中，我们首先对每个任务进行简要介绍，然后详细介绍如何利用扩散模型来提升性能。 我们在表 4 中总结了所有使用扩散模型的应用。

7.1 计算机视觉

7.1.1 图像生成

图像超分辨率和修复（Image Super Resolution and Inpainting）。图像超分辨率旨在从低分辨率 (LR) 图像中恢复高分辨率 (HR) 图像，而图像修复则是重建图像中缺失或损坏的区域。超分辨率扩散 (SRDiff) [119] 是基于扩散的单图像超分辨率模型，通过数据可能性的变分界限进行了优化。 SRDiff 能够通过对带有马尔可夫链的 LR 输入的高斯噪声进行逐步变换，从而提供多样化和逼真的超分辨率 (SR) 结果。 通过反复优化实现超分辨率（Super-Resolution via Repeated Refinement, SR3) [177] 采用去噪扩散概率模型[78, 186]进行条件图像生成，并通过随机迭代去噪过程进行图像超分辨率。 LDM [173] 提出了隐扩散模型，这是一种在不损失质量的情况下提高去噪扩散模型的训练和采样效率的有效方法。为了帮助使用有限的计算资源进行扩散模型训练，同时保持质量和灵活性，LDM 还通过预训练的自动编码器在隐空间中利用它们。 RePaint [130] 设计了一种改进的去噪策略，通过重采样迭代来更好地调节图像。 RePaint 并没有减慢扩散过程 [46]，而是在扩散过程中前进和后退，产生语义上有意义的图像。 Palette [175] 提出了一个基于条件扩散模型的统一框架，并在四个具有挑战性的图像生成任务 [91] 上对该框架进行了评估，例如着色、修复、取消裁剪和 JPEG 恢复。级联扩散模型 (CDM) [79] 由级联多个扩散模型组成，这些模型生成分辨率逐渐增加的图像。 CDM 能够在类别条件 ImageNet [43] 下在基准数据集上生成高质量图像，而无需来自辅助图像分类器的任何监督信息。多速扩散 (MSDiff) [12] 产生条件多速扩散估计器 (CMDE)，它是条件分数的估计器，它结合了以前的条件分数估计方法 [177, 200]。此外，还有一些工作将扩散模型应用于医学图像去噪和超分辨率 [32, 34, 157, 194]。

语义分割（Semantic Segmentation）。语义分割是对图像中属于同一类别的部分进行聚类。预训练可以提高语义分割模型的标签利用率，预训练语义分割模型的另一种方法是生成建模。最近的一项研究 [11] 调查了最先进的 DDPM [78] 学习的表示（representations），并证明它可以捕获对下游视觉任务有价值的高级语义信息。它在少样本（few-shot）操作点开发了一种简单的方法，该方法利用了这些学习到的表示，并显着优于包括 VDVAE [29] 和 ALAE [159] 在内的替代方案。受扩散模型成功的启发，学者们还研究了通过去噪自动编码器 [207] 学习的表示在语义分割中的有效性。解码器去噪预训练 (DDeP) [6] 使用监督学习过程初始化编码器，并仅预训练由去噪目标引导的解码器。

点云完成和生成（Point Cloud Completion and Generation）。3D 点云是用于捕获真实世界 3D 对象的 3D 表示的关键形式。然而，由于部分观察和自遮挡问题，现实世界中扫描的点云通常是不完整的。能够通过推理许多下游任务的缺失部分来恢复完整形状非常重要，包括 3D 重建、增强现实 (AR) 和场景理解 [140]。概率模型捕获了生成或完成问题的不确定性、多模态性质：它可以从头或部分观察中采样并产生不同的形状[136]。 PVD [253] 将去噪扩散模型与 3D 形状的点体素表示相结合。受非平衡热力学中扩散过程的启发，[135] 将点云中的点视为与热浴相关的热力学系统中的粒子，这使得从原始分布扩散到噪声分布。 Point Diffusion-Refinement (PDR) [140] 利用条件 DDPM 在给定部分观察的情况下生成粗略补全，并在生成的点云和统一的真值（ground truth）之间构建一对一的逐点映射。随后，其优化均方误差损失以实现均匀生成。

7.1.2 视频生成

在深度学习时代，由于视频帧的时空连续性和复杂性[233, 242]，高质量视频的生成仍然具有挑战性。最近的研究采用了扩散模型来提高生成视频的质量。灵活扩散模型 (FDM) [76] 提出了一种基于 DDPM 的新视频生成框架，可在不同的现实场景中生成长期视频完成。它引入了一个生成模型，可以在测试期间对任何其他子集上的视频帧的任意子集进行采样，并提出了一种为此目的而设计的体系结构。受神经视频压缩 [236] 最新进展的启发，残差视频扩散 (RVD) [235] 提出了一种自回归、端到端优化的视频扩散模型。它通过使用逆扩散过程生成的随机残差来校正确定性下一帧预测，从而连续生成未来帧。视频扩散模型（VDM）[81]引入了一种用于时空视频扩展的条件采样方法。它的性能优于先前提出的方法，并且可以生成较长、更高分辨率的视频。

7.2 自然语言处理

自然语言处理（Natural language processing）是旨在理解、建模和管理人类语言的研究领域。文本生成，也称为自然语言生成，已经成为自然语言处理中最关键和最具挑战性的任务之一[90]。它的目的是在给定输入数据（例如，序列和关键字）或随机噪声的情况下，用人类语言生成看似合理且可读的文本。研究人员开发了多种技术，广泛应用于文本的生成[121，121]。离散去噪扩散概率模型（D3PMs）[7]为字符级文本生成引入了类似扩散的生成模型[25]。他们通过超越具有均匀转移概率的腐败过程（corruption processes），推广了多项式扩散模型[85]。

大型自回归语言模型（LMs）能够生成高质量的文本[20，31，164，247]。为了在实际应用中可靠地部署这些LM，文本生成过程通常是可控的。这意味着我们需要生成能够满足所需要求的文本（例如主题、句法结构）。在不重新训练的情况下，控制语言模型 (LM) 的行为是文本生成中的一个主要且重要的问题 [39, 102]。尽管最近的工作在控制简单句子属性（如情感）方面取得了显著的成功[111，231]，但在复杂的细粒度控制（如句法结构）方面进展甚微。为了处理更复杂的控制，Diffusion LM[123]提出了一种基于连续扩散的新语言模型。扩散LM从一系列高斯噪声矢量开始，并逐步使其成为与单词对应的矢量。逐步去噪步骤有助于生成层次连续的隐式表示。这种层次连续的隐变量可以使简单的基于梯度的方法实现复杂的控制。模拟位（Analog Bits）[28]生成模拟位来表示离散变量，并通过自我调节和非对称时间间隔进一步提高样本质量。

7.3 波形信号处理

在电子学、声学和一些相关领域中，信号的波形通过图形形状来表示，它是时间的函数，与时间和量级无关。波形生成模型在语音生成任务中非常重要。WaveGrad [26] 引入了用于估计数据密度梯度的波形生成条件模型。该模型是在先验分数匹配和扩散概率模型的基础上构建的。它接收高斯白噪声信号作为输入，并使用基于梯度的采样器迭代地细化信号。WaveGrad通过调整细化步骤的数量，自然地用推理速度换取样本质量，并在音频质量方面建立起非自回归模型和自回归模型之间联系。DiffWave[110]为有条件或无条件波形生成提供了一个通用且强大的扩散概率模型。该模型是非自回归的，通过优化数据似然的变分界变量，可以有效地训练该模型。此外，它可以在不同的波形生成任务中生成高保真音频，例如类型条件生成和无条件生成。

7.4 多模态学习

7.4.1 文本到图像的生成

由于潜在应用的数量众多，视觉语言模型最近吸引了很多关注[163]。文本到图像生成是从描述性文本生成相应图像的任务[51]。混合扩散[8]利用预先训练的DDPM[45]和CLIP[163]模型，提出了一种通用的基于区域的图像编辑解决方案，该解决方案使用自然语言指导，适用于真实和多样的图像。unCLIP[165]提出了一个两阶段模型，一个先前的模型可以生成基于CLIP的、以文本标题为条件的图像嵌入，另一个基于扩散的解码器可以生成以图像嵌入为条件的图片。Imagen[176]提出了一种文本到图像的扩散模型，它具有更好的语言理解能力和前所未有的真实感。受引导扩散模型[45,80]生成照片级真实感样本的能力以及文本到图像模型处理自由形式提示的能力的启发，GLIDE[148]将引导扩散应用于文本条件图像合成的应用。VQ Diffusion[71]提出了一种用于文本到图像生成的矢量量化扩散模型，它消除了单向偏差并避免了累积预测误差。

7.4.2 文本到音频的生成

文本到音频生成是将正常语言文本转换为语音输出的任务[118，124，219]。Grad TTS[160]提出了一种新的文本到语音模型，该模型具有基于分数的解码器和扩散模型。它逐渐转换编码器预测的噪声，并通过单调对齐搜索方法进一步与输入的文本对齐[162]。Grad-TTS2[104]以自适应方式改进了Grad-TTS。Diffsound[229]提出了一种基于离散扩散模型的非自回归解码器[7186]，它在每个步骤中预测所有梅尔频谱（mel-spectrogram）符号，然后在以下步骤中细化预测的符号。EdiTTS[198]利用基于分数的文本到语音模型，在对mel谱图进行粗修改之前对其进行细化。ProDiff[88]通过直接预测干净数据，将去噪扩散模型参数化，而不是估计数据密度的梯度。

7.5 分子图建模

图形神经网络[73，221，234，252]和相应的表示学习[74]技术在许多领域取得了巨大成功[16，201，220，227，232，255]，包括在从属性预测[53，63]到分子生成[94，183]的各种任务中建模分子图，其中分子由节点边图自然表示。尽管它们在不同的应用中都很有效，但更多的内在和信息特性开始与扩散模型相结合，以增强分子图建模。扭转扩散[95]提出了一个新的扩散框架，该框架利用超空间上的扩散过程在扭转角空间上进行操作，并提出了一种从外在到内在的评分模型。等变扩散[82]提出了一种三维分子生成的扩散模型，该模型与欧氏变换等变。另一个等变扩散模型[3]为蛋白质结构和序列提出了一个完全数据驱动的去噪扩散概率模型，该模型能够在蛋白质数据库（PDB）的所有域中生成高度真实的蛋白质[15]。受模拟分子动力学的经典力场方法的启发，ConfGF[182]直接估计了分子构象生成中原子坐标对数密度的梯度场。动态图形分数匹配（DGSM）[137]根据原子在训练和测试过程中的空间相关性动态构建原子之间的图形结构，从而可以为预测分子构象的局部和远程交互建模。几何扩散[228]将每个原子视为一个粒子，并学习将扩散过程逆转为马尔可夫链。模体支架问题的一般解决方案[202]提出了一个3D蛋白质骨架生成模型，能够生成结构上与AlphaFold2[97]预测一致的骨架样本。

7.6 时间序列建模

7.6.1 时间序列插补

时间序列数据广泛用于许多重要的现实应用[54, 155, 233, 248]。然而，由于多种原因，时间序列通常包含缺失值，这些原因是由机械或人为错误引起的[185, 199, 238]。近年来，基于深度神经网络的插补方法在确定性插补[22, 24, 139]和概率插补[57]方面都取得了显著的成功。这些插补方法通常利用一种不同形式的自回归模型来处理时间序列，最近的工作已经开始利用强大的扩散模型来处理这个问题。CSDI[200]提出了一种新的时间序列插补方法，该方法利用了基于分数的扩散模型。具体来说，为了利用时间数据中的相关性，它采用了自我监督训练的形式来优化扩散模型。它在一些实际数据集中的应用表明了它优于以前的方法。CSDE[158]提出了一种新的概率框架，用于用神经控制的随机微分方程建模随机动力学。SSSD[2]集成了条件扩散模型和结构化状态空间模型[70]，以特别捕获时间序列中的长期依赖关系。它在时间序列插补和预测任务中都表现良好。

7.6.2 时间序列预测

时间序列预测是在一段时间内预报或推测未来值的任务。神经方法最近被广泛用于解决单变量点预测方法[154]或单变量概率方法[179]的预测问题。在多元设置中，我们也有点预测方法[122]和概率方法，它们使用高斯copulas[180]、GANs[240]或归一化流[168]明确建模数据分布。TimeGrad[167]提出了一种预测多元概率时间序列的自回归模型，该模型通过估计其梯度从每个时间步的数据分布中抽样。为此，它使用了扩散概率模型，该模型与分数匹配和基于能量的方法密切相关。具体来说，TimeGrad通过优化数据可能性的变分界限来学习梯度，并在推理期间使用Langevin采样[191]，通过马尔可夫链将白噪声转换为兴趣分布的样本。

7.7 对抗性净化

对抗净化[18，150，210，218，239]表示一类使用生成模型消除对抗干扰的防御方法[150]。虽然对抗性训练[142]被视为针对图像分类器的对抗性攻击的标准防御方法，但对抗性净化作为替代防御方法[239]表现出了显著的性能，它使用独立的净化模型将受攻击的图像净化为干净的图像。举一个对抗性的例子，DiffPure[150]在前向扩散过程之后用少量噪声对其进行扩散，然后用反向生成过程恢复干净的图像。自适应去噪净化（ADP）[239]表明，使用去噪分数匹配（DSM）训练的基于能量的模型EBM可以在短短几个steps内有效净化受攻击的图像。它进一步提出了一种有效的随机净化方案，在净化前向图像中注入随机噪声。投影梯度下降（PGD）[17]提出了一种新的基于随机扩散的预处理鲁棒化，旨在成为一种模型无关的对抗性防御，并产生高质量的去噪结果。

一些工作建议将引导扩散过程应用于高级对抗性净化。净化引导扩散模型（GDMP）[210]将净化纳入DDPM的扩散去噪过程；因此，它的扩散过程可以用逐渐增加的高斯噪声淹没对抗性扰动，并且可以通过引导去噪过程同时消除这两种噪声。[218]揭示了基于非制导扩散模型的对抗性净化和随机平滑技术之间的基本关联，从而产生了可证明的防御机制。

8.未来方向

重新审视实际情况（Re-Examining Practical Conditions）。我们仍然需要检查扩散模型中一些普遍相信的前提条件。例如，在实践中，人们普遍认为扩散模型的正向过程会将数据转换为标准高斯噪声。然而，前向扩散SDE的有限时间解仍然记得原始数据的分布。[58]对此问题进行了研究，但其结果只有在能够准确估计分数函数时才有效。因此，需要在长期扩散和短期扩散之间进一步考虑权衡。长期扩散确保扰动数据分布接近给定的先验值，而短扩散时间可以减少拟合误差和采样时间。然而，理想条件很难获得，因此，实际操作会导致不匹配的问题。我们应该认识到这种情况，并设计适当的扩散模型。

从离散时间到连续时间（From Discrete to Continuous Time）。由于扩散模型的灵活性，许多经验方法可以通过进一步分析得到加强[9，99，103，192]。例如，研究发现，分析连续时间扩散模型可以获得更好的样本质量[7，21]。因此，可以将离散时间扩散模型转换为相应的连续时间扩散模型，然后对模型进行分析和设计。这一研究方向很有前景，特别是当已经在离散时间设置中确定了噪声类型和时间表[9，21]的时候。

新一代程序（New Generation Procedure）。扩散模型通过两种主要的方法生成样本：一种是离散逆扩散SDE，然后通过离散逆SDE生成样本；另一种是在逆过程中利用马尔可夫链的性质对样本进行逐步去噪。然而，对于一些扩散模型，在实际中很难应用这些方法生成样本。例如，离散状态扩散模型很难找到对应的反向SDE，因为这些扩散模型通常利用随机游走或噪声遮罩（masking noises），因此在不引入额外方差的情况下无法估计反向扩散链的转换核。因此，应进一步研究新一代程序[7, 9, 40, 184, 189]。

推广到复杂场景和更多研究领域（Generalizing to Complex Scenarios and More Research Areas）。 如第 7 节所示，从计算机视觉到对抗性纯化，扩散模型已应用于七种不同类型的场景。 然而，仍然存在一些未充分探索的场景[211]，例如文本到视听语音合成[37]和视觉问答[5]。 此外，我们明显可以发现，大多数现有的应用程序仅限于单一输入/输出或简单输入/输出。 因此，对于研究人员来说，使扩散模型能够处理复杂的输入并生成多个输出，并在现实世界场景中获得更好的性能是至关重要且具有挑战性的。 尽管现已在鲁棒学习、代表性学习和强化学习等一些研究领域对扩散模型进行了研究，但其仍然存在与更多研究领域联系的机会 [143, 208]。

9.总结

在本文中，我们提出了扩散模型及其应用的新系统分类法。 具体来说，针对扩散模型增强的不同方面，我们将现有的扩散模型分为三类：采样加速、似然最大化和数据泛化。 此外，我们将扩散模型的应用分为七类：计算机视觉、自然语言处理、波形信号处理、多模态学习、分子图生成、时间序列建模和对抗性纯化。 最后，我们就算法和应用程序中的扩散模型的发展提出了新的观点。

参考文献略，请见原文。