传送门:
请点击我
如果点击有误:https://github.com/LeBron-Jian/DeepLearningNote
在整理这些知识点之前,我建议先看一下原论文,不然看我这个笔记,感觉想到哪里说哪里,如果看了论文,还有不懂的,正好这篇博客就是其详细解析,包括源码解析。
我翻译的链接:
下面开始:
1,Siamese Network 名字的由来
(名字的由来参考博客:https://www.jianshu.com/p/92d7f6eaacf5)
Siamese和Chinese有点像。Siam是古时候泰国的称呼,中文译作暹罗(xianluo)。Siamese也就是“暹罗”人或“泰国”人。Siamese在英语中是“孪生”、“连体”的意思,这是为什么呢?
十九世纪泰国出生了一对连体婴儿,当时的医学技术无法使两人分离出来,于是两人顽强地生活了一生,1829年被英国商人发现,进入马戏团,在全世界各地表演,1839年他们访问美国北卡罗莱那州后来成为“玲玲马戏团” 的台柱,最后成为美国公民。1843年4月13日跟英国一对姐妹结婚,恩生了10个小孩,昌生了12个,姐妹吵架时,兄弟就要轮流到每个老婆家住三天。1874年恩因肺病去世,另一位不久也去世,两人均于63岁离开人间。两人的肝至今仍保存在费城的马特博物馆内。从此之后“暹罗双胞胎”(Siamese twins)就成了连体人的代名词,也因为这对双胞胎让全世界都重视到这项特殊疾病。
回到孪生网络,简单来说,Siamese Network 就是“连体的神经网络”,神经网络的“连体”是通过共享权值来实现的。如下图:
孪生网络是一种特殊类型的神经网络架构。与一个学习对其输入进行分类的模型不同,该神经网络是学习在两个输入中进行区分。它学习了两个输入之间的相似之处。
当我们在做单样本分类任务的时候,网络可以比较测试集与训练集中的每张图片,然后挑选出哪一张与他最可能是同样类别。所以我们想让神经网络架构同时输入两张图片,输出他们属于同一个类别的概率。
假设 x1 和 x2是数据集中的两个类别,我们让 x1•x2 表示 x1 和 x2 是同一个类别。注意 x1•x2 与 x2•x1 是等价的——这意味着如果我们颠倒输入图片的顺序,输出的概率是完全相等的——p( x1•x2 ) 与 p( x2•x1 ) 相等。这被称为对称性,孪生网络就是依赖他设计的。
对称性是非常重要的,因为他要学习一个距离度量——x1到 x2 的距离应该等于 x2 到 x1的距离。
如果我们仅仅把两个样本拼接起来,把它作为神经网络的单一的输入,每个样本将会是与一个不同权重集合的矩阵相乘(或缠绕),这会打破对称性。没问题,这样子网络依然能成功的为每个输入学习到完全相对的权重,但是对两个输入学习相等的权重集合会更容易一些。所以我们可以让两个输入通过完全相对共享参数的网络,然后使用绝对差分作为线性分类器的输入——这是孪生网络必须的结构。两个完全相等的双胞胎,共用一个头颅,这就是孪生网络的由来。感觉放这个图再切实不过了。
 2,孪生神经网络的疑问及用途
2,孪生神经网络的疑问及用途
孪生神经网络是一类包含两个或更多个相同子网络的神经网络架构。这里相同是指他们具有相同的配置即相同的参数和权重。参数更新在两个子网上共同进行。
孪生神经网络在涉及发现相似性或两个可比较的事物之间的关系的任务中留下。一些例子是复述评分,其中输入是两个句子,输出是他们是多么相似的得分;或者签名验证,确定两个签名是否来自同一个人。通常,在这样的任务中,使用两个相同的子网络来处理两个输入,并且另一个模型将取得他们的输出并产生最终输出。
2.1,共享权值是什么?左右两个神经网络的权重一模一样吗?
答:是的,在代码实现的时候,甚至可以是同一个网络,不用实现另外一个,因为权值都一样。对于Siamase network,两边可以是lstm或者 cnn,都可以。
2.2,如果左右两边不共享权值,而是两个不同的神经网络,叫什么呢?
答:pseudo-siamese network,伪孪生神经网络,如下图所示,对于pseudo-siamese network ,两边可以是不同的神经网络(如一个是 lstm,一个是cnn)也可以是相同类型的神经网络。
2.3,孪生神经网络的用途是什么呢?
简单来说,衡量两个输入的相似程度。孪生神经网络有两个输入(Input1 and input2),将两个输入 feed 进入两个神经网络(Network1 and Network2),这两个神经网络分别将输入映射到新的空间,形成输入在新的空间中的表示。通过Loss的计算,评价两个输入的相似度。
据知乎作者查到的资料,养乐村同志在NIPS 1993上发表了论文《Signature Verification using a ‘Siamese’ Time Delay Neural Network》用于美国支票上的签名验证,即验证支票上的签名与银行预留签名是否一致。1993年,养乐村同志就在用两个卷积神经网络做签名验证了。
下面的图片来自于Bromley et al (1993)[1],他们为签名验证任务提出了一个孪生体系结构。
又比如在人脸领域,输入两个人的人脸图片信息,两个网络分别提取这两个人脸图片中不同的部分。在图中的网络,左右两个网络的作用是用于提取输入图片的特征。即特征提取器
我们通过使用两个网络提取出来了两个图片的特征,然后我们需要计算特征之间的差距distance,之后返回网络的输出结果,看两张图片是否属于同一个人。
2.4,孪生神经网络和伪孪生神经网络分别适用于什么场景呢?
孪生神经网络用于处理两个输入“比较类似”的情况。伪孪生神经网络适用于处理两个输入“
有一定差别
”的情况。比如,我们要计算两个句子或者词汇的语义相似度,使用 Siamese Network 比较适合;如果验证标题与正文描述是否一致(标题和正文长度差别很大),或者文字是否描述了一幅图片(一个是图片,一个是文字),就应该使用 pseudo-siamese network。也就是说要根据具体的应用,判断应该使用哪一种结构,哪一种Loss。
2.5,Siamese Network loss function 一般用哪一种呢?
Softmax 当然是一种好的选择,但是不一定是最优选择,即使在分类问题中。传统的Siamese Network使用Contrastive Loss。损失函数还有更多的选择,Siamese Network的初衷是计算两个输入的相似度,。左右两个神经网络分别将输入转换成一个"向量",在新的空间中,通过判断cosine距离就能得到相似度了。Cosine是一个选择,exp function也是一种选择,
欧式距离什么的都可以
,
训练的目标是让两个相似的输入距离尽可能的小,两个不同类别的输入距离尽可能的大
。其他的距离度量没有太多经验,这里简单说一下cosine和exp在NLP中的区别。
根据实验分析,cosine更适用于词汇级别的语义相似度度量,而exp更适用于句子级别、段落级别的文本相似性度量。其中的原因可能是cosine仅仅计算两个向量的夹角,exp还能够保存两个向量的长度信息,而句子蕴含更多的信息。
2.6,Siamese Network是双胞胎连体,整一个三胞胎连体可以不?
这个问题其实已经有人做过了,叫Triplet Network,论文是《Deep metric learning using Triplet network》,输入是三个,一个正例 + 两个负例,或者一个负例 + 两个正例,训练的目的是让相同类别间的距离尽可能的小,让不同类别间的距离尽可能的大。Triplet 在cifar,mnist的数据集上,效果都是很不错的,超过了Siamese Network。
Triplet Network 图如下:
2.7,Siamese Network 的用途有哪些?
这个可以说太多了,nlp&cv领域都有很多应用。
前面提到的词汇的语义相似度分析,QA中question和answer的匹配,签名/人脸验证。
手写体识别也可以用siamese network,网上已有github代码。
还有kaggle上Quora的question pair的比赛,即判断两个提问是不是同一问题,冠军队伍用的就是n多特征+Siamese network。
在图像上,基于Siamese网络的视觉跟踪算法也已经成为热点《
Fully-convolutional siamese networks for object tracking
》。
3,Siamese Network 概述
Siamese Network 是一种神经网络的架构,而不是具体的某种网络,就像Seq2Seq一样,具体实现上可以使用RNN也可以使用CNN。
Siamese Network 就像“连体的神经网络”,神经网络的“连体”是通过共享权值来实现的(共享权值即左右两个神经网络的权重一模一样)
Siamese Network的作用就是衡量两个输入的相似程度。孪生神经网络有两个输入(input1 and input2),将两个输入 feed 进入两个神经网络(Network1 andNetwork2),这两个神经网络分别将映射到新的空间,形成输入在新的空间中的表示。通过Loss的计算,评价两个输入的相似度。
Siamese Network和其他网络的不同之处就在于,首先他是两个输入,他输入的不是标签,而是是否是同一类别,如果是同一类别就是0,否则就是1。
4,Contrastive Loss 损失函数
孪生架构的目的不是对输入图像进行分类,而是区分它们。因此,分类损失函数(如交叉熵)不是最合适的选择。相反,这种架构更适合使用对比函数。根据直觉而言,这个函数只是评估网络区分一对给定的图像的效果如何。
在传统的孪生神经网络(Siamese Network)中,其采用的损失函数时Contrastive Loss,这种损失函数可以有效的处理孪生神经网络中的 paired data的关系。contrastive loss 的表达式如下:
Dw被定义为孪生网络的输出之间的欧式距离,代表两个样本特征 X1 和 X2 的欧式距离(二范数)P表示样本的特征维数,Y表示两个样本是否匹配的标签,Y=1代表两个样本相似或者匹配,Y=0代表不匹配,m即margin为设定的阈值。
所以对于孪生神经网络而言,当输入的是同一张图片的时候,我们希望他们之间的欧式距离很小,损失也越小;当不是同一张图片的时候,欧式距离很大,损失也很大。简单来说就是我们要最小化相同类的数据之间的距离,最大化不同类之间的距离。而观察上述的 Contrastive Loss 的表达式可以发现,这种损失函数可以很好的表达成对样本的匹配程度,也能够很好地用于训练提取特征的模型。
当Y=1(即样本相似时),损失函数只剩下:
即当样本相似时,如果在特征空间的欧式距离较大,则说明当前的模型不好,因此加大损失。
当Y=0(即样本不相似时),损失函数为:
即当样本不相似时,其特征空间的欧式距离反而小的话,损失值会变大,这也正好符合我们的要求。
注意:这里设置了一个阈值 margin,表示我们只考虑不相似特征欧式距离在 0~margin之间的,当距离超过 margin的,则把其loss看做为 0 (即不相似的特征离的很远,其 loss 应该是很低的;而对于相似的特征反而离的很远,我们就需要增加其 loss, 从而不断更新成对样本的匹配程度)
下面这张图就是损失函数值与样本特征的欧式距离之间的关系,其中红线虚线表示的是相似样本的损失值,蓝色实现表示的是不相似样本的损失值。
5,网络架构
Koch 等人使用卷积孪生网络去分类成对的Omniglot图像,所以这两个孪生网络都是卷积神经网络。这两个孪生网络每个的架构如下:64通道的10*10卷积核,relu -> max pool -> 128 通道的 7*7 卷积核, relu -> max pool -> 128 通道的 4*4 卷积核,relu -> max pool -> 256通道的 4*4 卷积核。孪生网络把输入降低到越来越小的3d张量上,最终他们经过一个 4096 神经元的全连接层。两个向量的绝对差作为线性分类器的输入。这个网络一共有 38951745 个参数——96%的参数属于全连接层。这个参数量很大,所以网络有很高的过拟合风险,但是成对的训练意味着数据集是很大的,所以过拟合问题不曾出现。
输出被归一化到 [0, 1]之间,使用 Sigmoid函数让它变成一个概率,当两个图像是相同类别的时候,我们使目标 t=1,类别不相同的时候 t=0,它使用Logistic回归来训练。这意味着损失函数应该是预测和目标之间的二分类交叉熵。损失函数中还有一个 L2 权重衰减项,以让网络可以学习更小的\更平滑的权重,从而提高泛化能力:
当网络做单样本学习的时候,孪生网络简单的分类一下测试图像与训练集中的图像中那个最相似就可以了:
这里使用argmax 而不是近邻方法中的 argmin,因为类别越不同,L2度量的值越高,但是这个模型的输出 p( x1•x2 ) ,所以我们要这个值最大。这个方法有一个明显的缺陷:对于训练集中的 Xa,概率 x1•x2 与训练集中每个样本都是独立的!这意味着概率值的和不为1.言归正传,测试图像与训练图像应该是相同类型的。。。
5.1逐对训练的有效的数据集大小
作者注意到:采用逐对训练的话,将会有平方级别对的图像对来训练模型,这让模型很难过拟合,很好。假设我们有 E 类,每类有 C 个样本。一共有 C•E 张图片,总共可能的配方数量可以这样计算:
对于 omniglot 中的 964类(每类20个样本),这会有 185849560 个可能的配对,这是巨大的!然而,孪生网络需要相同类的和不同类的配对都有。每类 E 个训练样本,所以每个类别有
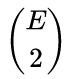 对,这意味着有
对,这意味着有
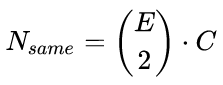 个相同类别的配对。对于 Omniglot 有 183160对。即使 183160对已经很大了,但他只是所有可能配对的千分之一,因为相同类别的配对数量随着 E平方级的增大,但是随着C是线性增加。这个问题非常重要,因为孪生网络训练的时候,同类别和不同类别的比例应该是1:1,或许它表明逐对训练在那种每个类别有更多样本的数据集上更容易训练。
个相同类别的配对。对于 Omniglot 有 183160对。即使 183160对已经很大了,但他只是所有可能配对的千分之一,因为相同类别的配对数量随着 E平方级的增大,但是随着C是线性增加。这个问题非常重要,因为孪生网络训练的时候,同类别和不同类别的比例应该是1:1,或许它表明逐对训练在那种每个类别有更多样本的数据集上更容易训练。
5.2 代码
下面是模型定义,如果你见过Keras,那很容易理解。这里只用 Sequential() 来定义一次孪生网络,然后使用两个输入层来调用它,这样两个输入使用相同的参数。然后我们把他们使用绝对距离合并起来,添加一个输出层,使用二分类交叉熵损失来编译这个模型。
# _*_coding:utf-8_*_
from keras.layers import Input, Conv2D, Lambda, merge, Dense, Flatten, MaxPooling2D
from keras.models import Model, Sequential
from keras.regularizers import l2
from keras import backend as K
from keras.optimizers import SGD, Adam
from keras.losses import binary_crossentropy
import numpy.random as rng
import numpy as np
import os
import dill as pickle
import matplotlib.pyplot as plt
from sklearn.utils import shuffle
import tensorflow as tf
def W_init(shape, name=None):
''' Initiallize weights as in paper'''
values = rng.normal(loc=0, scale=1e-2, size=shape)
return K.variable(values, name=name)
# //TODO figure out how to initialize layer biases in keras
def b_init(shape, name=None):
"""Initialize bias as in paper"""
values = rng.normal(loc=0.5, scale=1e-2, size=shape)
return K.variable(values, name=name)
input_shape = (105, 105, 1)
left_input = Input(input_shape)
right_input = Input(input_shape)
# build convnet to use in each siamese 'leg'
convnet = Sequential()
convnet.add(Conv2D(64, (10, 10), activation='relu', input_shape=input_shape,
kernel_initializer=W_init, kernel_regularizer=l2(2e-4)))
convnet.add(MaxPooling2D())
convnet.add(Conv2D(128, (7, 7), activation='relu',
kernel_regularizer=l2(2e-4), kernel_initializer=W_init, bias_initializer=b_init))
convnet.add(MaxPooling2D())
convnet.add(Conv2D(128, (4, 4), activation='relu', kernel_initializer=W_init, kernel_regularizer=l2(2e-4),
bias_initializer=b_init))
convnet.add(MaxPooling2D())
convnet.add(Conv2D(256, (4, 4), activation='relu', kernel_initializer=W_init, kernel_regularizer=l2(2e-4),
bias_initializer=b_init))
convnet.add(Flatten())
convnet.add(
Dense(4096, activation="sigmoid", kernel_regularizer=l2(1e-3), kernel_initializer=W_init, bias_initializer=b_init))
# encode each of the two inputs into a vector with the convnet
encoded_l = convnet(left_input)
encoded_r = convnet(right_input)
# merge two encoded inputs with the l1 distance between them
L1_distance = lambda x: K.abs(x[0] - x[1])
both = merge([encoded_l, encoded_r], mode=L1_distance, output_shape=lambda x: x[0])
prediction = Dense(1, activation='sigmoid', bias_initializer=b_init)(both)
siamese_net = Model(input=[left_input, right_input], output=prediction)
# optimizer = SGD(0.0004,momentum=0.6,nesterov=True,decay=0.0003)
optimizer = Adam(0.00006)
# //TODO: get layerwise learning rates and momentum annealing scheme described in paperworking
siamese_net.compile(loss="binary_crossentropy", optimizer=optimizer)
siamese_net.count_params()
原论文中每个层的学习率和冲量都不相同,因为使用Keras来实现这个太麻烦,并且超参数不是重点。Koch等人增加向训练集中增加失真的图像,使用 150000 对样本训练模型。因为这个太大了,我的内存放下下,所以我决定使用随机采样的方法。载入图像对或许是这个模型最难实现的部分,因为这里每个类别有20个样本,我们把数据调整为 N_Classes*20*105*105 的数组,这样可以很方便的来索引。
class Siamese_Loader:
"""For loading batches and testing tasks to a siamese net"""
def __init__(self, Xtrain, Xval):
self.Xval = Xval
self.Xtrain = Xtrain
self.n_classes, self.n_examples, self.w, self.h = Xtrain.shape
self.n_val, self.n_ex_val, _, _ = Xval.shape
def get_batch(self, n):
"""Create batch of n pairs, half same class, half different class"""
categories = rng.choice(self.n_classes, size=(n,), replace=False)
pairs = [np.zeros((n, self.h, self.w, 1)) for i in range(2)]
targets = np.zeros((n,))
targets[n // 2:] = 1
for i in range(n):
category = categories[i]
idx_1 = rng.randint(0, self.n_examples)
pairs[0][i, :, :, :] = self.Xtrain[category, idx_1].reshape(self.w, self.h, 1)
idx_2 = rng.randint(0, self.n_examples)
# pick images of same class for 1st half, different for 2nd
category_2 = category if i >= n // 2 else (category + rng.randint(1, self.n_classes)) % self.n_classes
pairs[1][i, :, :, :] = self.Xtrain[category_2, idx_2].reshape(self.w, self.h, 1)
return pairs, targets
def make_oneshot_task(self, N):
"""Create pairs of test image, support set for testing N way one-shot learning. """
categories = rng.choice(self.n_val, size=(N,), replace=False)
indices = rng.randint(0, self.n_ex_val, size=(N,))
true_category = categories[0]
ex1, ex2 = rng.choice(self.n_examples, replace=False, size=(2,))
test_image = np.asarray([self.Xval[true_category, ex1, :, :]] * N).reshape(N, self.w, self.h, 1)
support_set = self.Xval[categories, indices, :, :]
support_set[0, :, :] = self.Xval[true_category, ex2]
support_set = support_set.reshape(N, self.w, self.h, 1)
pairs = [test_image, support_set]
targets = np.zeros((N,))
targets[0] = 1
return pairs, targets
def test_oneshot(self, model, N, k, verbose=0):
"""Test average N way oneshot learning accuracy of a siamese neural net over k one-shot tasks"""
n_correct = 0
if verbose:
print("Evaluating model on {} unique {} way one-shot learning tasks ...".format(k, N))
for i in range(k):
inputs, targets = self.make_oneshot_task(N)
probs = model.predict(inputs)
if np.argmax(probs) == 0:
n_correct += 1
percent_correct = (100.0 * n_correct / k)
if verbose:
print("Got an average of {}% {} way one-shot learning accuracy".format(percent_correct, N))
return percent_correct
下面是训练过程了。没什么特别的,除了我监测的时验证机精度来测试性能,而不是验证集上的损失。
evaluate_every = 7000
loss_every=300
batch_size = 32
N_way = 20
n_val = 550
siamese_net.load_weights("PATH")
best = 76.0
for i in range(900000):
(inputs,targets)=loader.get_batch(batch_size)
loss=siamese_net.train_on_batch(inputs,targets)
if i % evaluate_every == 0:
val_acc = loader.test_oneshot(siamese_net,N_way,n_val,verbose=True)
if val_acc >= best:
print("saving")
siamese_net.save('PATH')
best=val_acc
if i % loss_every == 0:
print("iteration {}, training loss: {:.2f},".format(i,loss))
5.3 结果
一旦学习曲线变平整了,我使用在20类验证集合上表现最好的模型来测试。我的网络在验证集上得到了大约83%的精度,原论文精度是93%,或许这个差别是因为我没有实现原论文中的很多增强性能的技巧,像逐层的学习率/冲量,使用数据失真的数据增强方法,贝叶斯超参数优化,并且其迭代次数也不够。但是没关系,这个教程侧重于简要介绍单样本的学习,而不是在其百分之几的分类性能上钻牛角尖。
5.4 讨论
现在我们只是训练了一个来做鉴别相同还是不同的二分类网络。更重要的是,我们展现了模型能够在没有见过的字母表上的20类单样本学习的性能。当然,这不是使用深度学习来做单样本学习的唯一方式。
正如前面提到的,孪生网络的最大缺陷是它要拿测试图像与训练集中图像逐个比较。当这个网络将测试图像与任何图像 x1 相比,不管训练集是什么,P(xhat*x1) 都是相同的。这很愚蠢,假如你在做单样本学习任务,你看到一张图片与测试图像非常类似。然而,当你看到训练中另外一张图片也与测试集非常相似,你就会对他的类别没有那么自信了。训练目标与测试目标是不同的,如果有一个模型可以很好地比较测试图片与训练集,并且使用仅仅有一个训练图片与之拥有相同类别的限制,那么模型会表现的更好。
Matching Networks for One Shot learning这篇论文就是做这个的。它们使用深度模型来端到端的学习一个完整的近邻分类器,而不是学习相似度函数,直接在单样本任务上训练,而不是在一个图像对上。Andrej Karpathy’s notes很好的解释了这个问题。因为你正在学习机器分类,所以你可以把他视为元学习(meta learning)。One-shot Learning with Memory-Augmented Neural Networks 这篇论文解释了单样本学习与元学习的关系,它在omniglot数据集上训练了一个记忆增强网络,然而,我承认我看不懂这篇论文。
6,Keras 实现Siamese Network
整理了这么多,就是说自己想学习Siamese network ,但是网上目前找到的资源就这么多,而且自己都整理出来了,大概也明白了其意义,了解了其损失函数,明白了网络架构原理。接下来就是练习的时刻了。
6.1 在MNIST数据集上训练Siamese network
既然都会了,那么就实践一下,首先,我们用mnist 数据集做实践,而这个的代码是keras官方给的,代码如下:
from __future__ import absolute_import
from __future__ import print_function
import numpy as np
import random
from keras.datasets import mnist
from keras.models import Model
from keras.layers import Input, Flatten, Dense, Dropout, Lambda
from keras.optimizers import RMSprop
from keras import backend as K
num_classes = 10
epochs = 20
def euclidean_distance(vects):
x, y = vects
sum_square = K.sum(K.square(x - y), axis=1, keepdims=True)
return K.sqrt(K.maximum(sum_square, K.epsilon()))
def eucl_dist_output_shape(shapes):
shape1, shape2 = shapes
return (shape1[0], 1)
def contrastive_loss(y_true, y_pred):
'''Contrastive loss from Hadsell-et-al.'06
http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf
margin = 1
square_pred = K.square(y_pred)
margin_square = K.square(K.maximum(margin - y_pred, 0))
return K.mean(y_true * square_pred + (1 - y_true) * margin_square)
def create_pairs(x, digit_indices):
'''Positive and negative pair creation.
Alternates between positive and negative pairs.
pairs = []
labels = []
n = min([len(digit_indices[d]) for d in range(num_classes)]) - 1
for d in range(num_classes):
for i in range(n):
z1, z2 = digit_indices[d][i], digit_indices[d][i + 1]
pairs += [[x[z1], x[z2]]]
inc = random.randrange(1, num_classes)
dn = (d + inc) % num_classes
z1, z2 = digit_indices[d][i], digit_indices[dn][i]
pairs += [[x[z1], x[z2]]]
labels += [1, 0]
return np.array(pairs), np.array(labels)
def create_base_network(input_shape):
'''Base network to be shared (eq. to feature extraction).
input = Input(shape=input_shape)
x = Flatten()(input)
x = Dense(128, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(128, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(128, activation='relu')(x)
return Model(input, x)
def compute_accuracy(y_true, y_pred):
'''Compute classification accuracy with a fixed threshold on distances.
pred = y_pred.ravel() < 0.5
return np.mean(pred == y_true)
def accuracy(y_true, y_pred):
'''Compute classification accuracy with a fixed threshold on distances.
return K.mean(K.equal(y_true, K.cast(y_pred < 0.5, y_true.dtype)))
# the data, split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
input_shape = x_train.shape[1:]
# create training+test positive and negative pairs
digit_indices = [np.where(y_train == i)[0] for i in range(num_classes)]
tr_pairs, tr_y = create_pairs(x_train, digit_indices)
digit_indices = [np.where(y_test == i)[0] for i in range(num_classes)]
te_pairs, te_y = create_pairs(x_test, digit_indices)
# network definition
base_network = create_base_network(input_shape)
input_a = Input(shape=input_shape)
input_b = Input(shape=input_shape)
# because we re-use the same instance `base_network`,
# the weights of the network
# will be shared across the two branches
processed_a = base_network(input_a)
processed_b = base_network(input_b)
distance = Lambda(euclidean_distance,
output_shape=eucl_dist_output_shape)([processed_a, processed_b])
model = Model([input_a, input_b], distance)
# train
rms = RMSprop()
model.compile(loss=contrastive_loss, optimizer=rms, metrics=[accuracy])
model.fit([tr_pairs[:, 0], tr_pairs[:, 1]], tr_y,
batch_size=128,
epochs=epochs,
validation_data=([te_pairs[:, 0], te_pairs[:, 1]], te_y))
# compute final accuracy on training and test sets
y_pred = model.predict([tr_pairs[:, 0], tr_pairs[:, 1]])
tr_acc = compute_accuracy(tr_y, y_pred)
y_pred = model.predict([te_pairs[:, 0], te_pairs[:, 1]])
te_acc = compute_accuracy(te_y, y_pred)
print('* Accuracy on training set: %0.2f%%' % (100 * tr_acc))
print('* Accuracy on test set: %0.2f%%' % (100 * te_acc))
结果如下:
106112/108400 [============================>.] - ETA: 0s - loss: 0.0101 - accuracy: 0.9903
107136/108400 [============================>.] - ETA: 0s - loss: 0.0100 - accuracy: 0.9903
108160/108400 [============================>.] - ETA: 0s - loss: 0.0101 - accuracy: 0.9903
108400/108400 [==============================] - 8s 75us/step - loss: 0.0101 - accuracy: 0.9903 - val_loss: 0.0263 - val_accuracy: 0.9730
* Accuracy on training set: 99.59%
* Accuracy on test set: 97.30%
分析结果,我们可以知道在MNIST数据集中,我们成对的训练Siamese Network,然后通过计算共享网络输出上的欧几里得距离,通过20个epochs 后,准确率达到了97.3%。
我们可以画出损失图,画损失图代码如下:
import matplotlib.pyplot as plt
def plot_training(history):
plt.figure(figsize=(8, 4))
plt.subplot(1, 2, 1)
train_acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
plt.plot(train_acc, '-o', label='train_acc')
plt.plot(val_acc, '-o', label='test_acc')
plt.xlabel('Epochs')
plt.legend()
plt.subplot(1, 2, 2)
train_acc = history.history['loss']
val_acc = history.history['val_loss']
plt.plot(train_acc, '-o', label='train_loss')
plt.plot(val_acc, '-o', label='test_loss')
plt.xlabel('Epochs')
plt.legend()
损失图如下:
下面对上面代码进行分析。
其实代码比较简单,Contrastive loss function 代码如下:
def contrastive_loss(y_true, y_pred):
'''Contrastive loss from Hadsell-et-al.'06
http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf
margin = 1
square_pred = K.square(y_pred)
margin_square = K.square(K.maximum(margin - y_pred, 0))
return K.mean(y_true * square_pred + (1 - y_true) * margin_square)
这是照着公式写的,就不多说。
而此模型,我们仔细观察,就是多层感知器,只不过是使用Keras的函数式完成的。
def create_base_network(input_shape):
'''Base network to be shared (eq. to feature extraction).
input = Input(shape=input_shape)
x = Flatten()(input)
x = Dense(128, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(128, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(128, activation='relu')(x)
return Model(input, x)
这个代码是一个三层的感知器,其实理解了代码之后,实现 n 层感知器都不是问题。所以只需要理解好这个三层的MLP模型即可。概况的说,MLP的输入层X其实就是我们的训练数据,而这里的处理就是Flatten 。输入层实现后,输入层到隐含层就是一个全连接的层,利用Dense() 函数(此函数为Keras内置的全连接层函数)即可。
下面要说的就是他数据的输入方式:
def create_pairs(x, digit_indices):
'''Positive and negative pair creation.
Alternates between positive and negative pairs.
pairs = []
labels = []
n = min([len(digit_indices[d]) for d in range(num_classes)]) - 1
for d in range(num_classes):
for i in range(n):
z1, z2 = digit_indices[d][i], digit_indices[d][i + 1]
pairs += [[x[z1], x[z2]]]
inc = random.randrange(1, num_classes)
dn = (d + inc) % num_classes
z1, z2 = digit_indices[d][i], digit_indices[dn][i]
pairs += [[x[z1], x[z2]]]
labels += [1, 0]
return np.array(pairs), np.array(labels)
从代码中,我们可以看出,它将数据绑成一对一对的,将两个同类的数据绑一起,用label 1表示;将两个不同类的照片绑一起,用label 0表示。前面5.1提到过数据两两组合有很多种方式,大概有平方级别的图像对。这里采用了一种巧妙的方法,就是将第n张图片与n+1张相同的照片绑一起,这样一来就避免了大量的图像对了。而且这种方式我们的图像是不需要标签的。我们的标签是函数里面设定好的,这个和传统的分类算法也是有区别的,简单来说就是这里输入的不是标签,而是是否是同一类别。
这里强调一下,使用图像对训练模型,这样模型就很难过拟合。
最后就是喂入数据,进行训练了,训练就不说了,和传统的分类是一样的。但是喂入数据还是不同的,是Siamese Network特有的方式,代码如下:
# network definition
base_network = create_base_network(input_shape)
input_a = Input(shape=input_shape)
input_b = Input(shape=input_shape)
processed_a = base_network(input_a)
processed_b = base_network(input_b)
distance = Lambda(euclidean_distance,
output_shape=eucl_dist_output_shape)([processed_a, processed_b])
model = Model([input_a, input_b], distance)
我们也看到过,上面只使用函数定义了一次网络,然后这里使用两个输入层(input_a, input_b)来调用它,这样两个输入使用相同的参数,然后feed进入相同的神经网络,这两个神经网络分别映射到新的空间(processed_a, processed_b)。然后我们需要将他们使用绝对距离合并起来,添加一个输出层(distance),最后使用二分类交叉熵来编译这个模型。
总体来说,使用Keras实现的话,代码简单,易于理解。
6.2 在自己的数据集上训练Siamese network
既然可以在MNIST的数据集训练数据,那么也可以在自己的数据集训练。这里我采用的数据集是五分类。
数据描述:
共有500张图片,分为大巴车、恐龙、大象、鲜花和马五个类,每个类100张。下载地址:http://pan.baidu.com/s/1nuqlTnN
我们先导入数据:
def get_image_data(imagePaths, label):
data = []
labels = []
for image_name in os.listdir(imagePaths):
imagePath = os.path.join(imagePaths, image_name)
image = cv2.imread(imagePath)
image = cv2.resize(image, target_size)
data.append(image)
labels.append(label)
data = np.array(data, dtype='float')
data /= 255.0
labels = np.array(labels)
data, labels = shuffle(data, labels, random_state=0)
return data, labels
def load_train_test_data():
filelist = []
for i in os.listdir(file_path):
filelist.append(i)
data = []
labels = []
for i in range(len(filelist)):
filedir = filelist[i]
allpath = os.path.join(file_path, filelist[i])
data_i, labels_i = get_image_data(imagePaths=allpath, label=filedir)
data_i, labels_i = list(data_i), list(labels_i)
data.extend(data_i)
labels.extend(labels_i)
data, labels = np.array(data), np.array(labels)
x_train, x_test, y_train, y_test = train_test_split(data, labels, test_size=0.2, random_state=123456)
return x_train, x_test, y_train, y_test, filelist
def load_data():
x_train, x_test, y_train, y_test, filelist = load_train_test_data()
print(x_train.shape, y_train.shape)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
# x_train /= 255.0
# x_test /= 255.0
input_shape = x_train.shape[1:] # (80, 80)
digit_indices = [np.where(y_train == filelist[i])[0] for i in range(num_classes)]
tr_pairs, tr_y = create_pairs(x_train, digit_indices)
digit_indices = [np.where(y_test == filelist[i])[0] for i in range(num_classes)]
te_pairs, te_y = create_pairs(x_test, digit_indices)
# print(te_pairs.shape, te_y.shape) # (980, 2, 80, 80) (980,)
return input_shape, tr_pairs, tr_y, te_pairs, te_y
然后我们使用MLP模型训练:
def create_base_network(input_shape):
'''Base network to be shared (eq. to feature extraction).'''
input = Input(shape=input_shape)
x = Flatten()(input)
x = Dense(128, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(128, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(128, activation='relu')(x)
return Model(input, x)
其他与上面类似,这里不重复贴了。结果如下:
- 2s - loss: 14.9671 - accuracy: 0.5171 - val_loss: 0.2103 - val_accuracy: 0.6643
Epoch 2/100
- 0s - loss: 0.2774 - accuracy: 0.5684 - val_loss: 0.2842 - val_accuracy: 0.5071
Epoch 3/100
- 0s - loss: 0.2781 - accuracy: 0.5776 - val_loss: 0.1577 - val_accuracy: 0.7643
Epoch 4/100
- 0s - loss: 0.4256 - accuracy: 0.5224 - val_loss: 0.1693 - val_accuracy: 0.7857
Epoch 5/100
- 0s - loss: 0.4215 - accuracy: 0.5224 - val_loss: 0.2731 - val_accuracy: 0.5214
Epoch 6/100
- 0s - loss: 0.4870 - accuracy: 0.5263 - val_loss: 0.3136 - val_accuracy: 0.6571
Epoch 7/100
- 0s - loss: 1.3985 - accuracy: 0.5211 - val_loss: 0.4132 - val_accuracy: 0.5000
Epoch 8/100
- 0s - loss: 1.0154 - accuracy: 0.5250 - val_loss: 0.1802 - val_accuracy: 0.7929
Epoch 9/100
- 0s - loss: 0.6538 - accuracy: 0.5382 - val_loss: 0.1928 - val_accuracy: 0.7429
Epoch 10/100
- 0s - loss: 0.3917 - accuracy: 0.5461 - val_loss: 0.2226 - val_accuracy: 0.6786
Epoch 11/100
- 0s - loss: 0.3202 - accuracy: 0.5737 - val_loss: 0.2040 - val_accuracy: 0.7000
Epoch 12/100
。。。。。。
Epoch 91/100
- 0s - loss: 0.1849 - accuracy: 0.7605 - val_loss: 0.1677 - val_accuracy: 0.7429
Epoch 92/100
- 0s - loss: 0.1782 - accuracy: 0.7816 - val_loss: 0.2753 - val_accuracy: 0.5857
Epoch 93/100
- 0s - loss: 0.2656 - accuracy: 0.6671 - val_loss: 0.1685 - val_accuracy: 0.7857
Epoch 94/100
- 0s - loss: 0.2607 - accuracy: 0.6684 - val_loss: 0.1785 - val_accuracy: 0.7643
Epoch 95/100
- 0s - loss: 0.1780 - accuracy: 0.7868 - val_loss: 0.1800 - val_accuracy: 0.7429
Epoch 96/100
- 0s - loss: 0.2324 - accuracy: 0.7263 - val_loss: 0.3307 - val_accuracy: 0.5071
Epoch 97/100
- 0s - loss: 0.1957 - accuracy: 0.7250 - val_loss: 0.1646 - val_accuracy: 0.7857
Epoch 98/100
- 0s - loss: 0.1809 - accuracy: 0.7605 - val_loss: 0.1704 - val_accuracy: 0.7643
Epoch 99/100
- 0s - loss: 0.2097 - accuracy: 0.7276 - val_loss: 0.1719 - val_accuracy: 0.7500
Epoch 100/100
- 0s - loss: 0.2314 - accuracy: 0.6842 - val_loss: 0.1709 - val_accuracy: 0.7786
* Accuracy on training set: 89.61%
* Accuracy on test set: 77.86%
看起来效果一般。
这里我将网络加深,修改后的网络如下:
def create_deep_network(input_shape, out_dims=num_classes):
inputs_dim = Input(shape=input_shape)
x = Conv2D(filters=32, kernel_size=3, strides=1, padding='same',
activation='relu')(inputs_dim)
x = Conv2D(filters=32, kernel_size=3, strides=1, padding='same',
activation='relu')(x)
x = MaxPooling2D(pool_size=(2, 2))(x)
x = Conv2D(filters=64, kernel_size=3, strides=1, padding='same',
activation='relu')(x)
x = Conv2D(filters=64, kernel_size=3, strides=1, padding='same',
activation='relu')(x)
x = MaxPooling2D(pool_size=(2, 2))(x)
x_flat = Flatten()(x)
fc1 = Dense(512, activation='relu')(x_flat)
dp_1 = Dropout(0.4)(fc1)
fc2 = Dense(out_dims)(dp_1)
fc2 = Activation('softmax')(fc2)
model = Model(inputs=inputs_dim, outputs=fc2)
return model
训练结果:
- 7s - loss: 0.2834 - accuracy: 0.6355 - val_loss: 0.2863 - val_accuracy: 0.5286
Epoch 2/100
- 2s - loss: 0.1638 - accuracy: 0.7829 - val_loss: 0.1462 - val_accuracy: 0.7714
Epoch 3/100
- 2s - loss: 0.1101 - accuracy: 0.8539 - val_loss: 0.1601 - val_accuracy: 0.7929
Epoch 4/100
- 2s - loss: 0.1067 - accuracy: 0.8592 - val_loss: 0.1240 - val_accuracy: 0.8143
Epoch 5/100
- 2s - loss: 0.0857 - accuracy: 0.8829 - val_loss: 0.1280 - val_accuracy: 0.8429
Epoch 6/100
- 2s - loss: 0.0714 - accuracy: 0.9132 - val_loss: 0.1148 - val_accuracy: 0.8214
Epoch 7/100
- 2s - loss: 0.0549 - accuracy: 0.9382 - val_loss: 0.0855 - val_accuracy: 0.8929
Epoch 8/100
- 2s - loss: 0.0408 - accuracy: 0.9658 - val_loss: 0.0671 - val_accuracy: 0.9214
Epoch 9/100
- 2s - loss: 0.0351 - accuracy: 0.9618 - val_loss: 0.0660 - val_accuracy: 0.9000
Epoch 10/100
- 2s - loss: 0.0253 - accuracy: 0.9750 - val_loss: 0.1011 - val_accuracy: 0.8714
Epoch 11/100
- 2s - loss: 0.0291 - accuracy: 0.9684 - val_loss: 0.0538 - val_accuracy: 0.9214
Epoch 12/100
- 2s - loss: 0.0231 - accuracy: 0.9803 - val_loss: 0.0621 - val_accuracy: 0.9214
Epoch 13/100
- 2s - loss: 0.0192 - accuracy: 0.9882 - val_loss: 0.0498 - val_accuracy: 0.9286
。。。。。。
Epoch 90/100
- 2s - loss: 2.3402e-05 - accuracy: 1.0000 - val_loss: 0.0120 - val_accuracy: 0.9929
Epoch 91/100
- 2s - loss: 1.4936e-05 - accuracy: 1.0000 - val_loss: 0.0127 - val_accuracy: 0.9929
Epoch 92/100
- 2s - loss: 2.3215e-05 - accuracy: 1.0000 - val_loss: 0.0148 - val_accuracy: 0.9857
Epoch 93/100
- 2s - loss: 0.0376 - accuracy: 0.9579 - val_loss: 0.1812 - val_accuracy: 0.8143
Epoch 94/100
- 2s - loss: 0.1855 - accuracy: 0.7987 - val_loss: 0.1621 - val_accuracy: 0.8143
Epoch 95/100
- 2s - loss: 0.1093 - accuracy: 0.8737 - val_loss: 0.1229 - val_accuracy: 0.8500
Epoch 96/100
- 2s - loss: 0.0875 - accuracy: 0.8987 - val_loss: 0.1216 - val_accuracy: 0.8571
Epoch 97/100
- 2s - loss: 0.0973 - accuracy: 0.8882 - val_loss: 0.1086 - val_accuracy: 0.8786
Epoch 98/100
- 2s - loss: 0.0883 - accuracy: 0.8947 - val_loss: 0.1234 - val_accuracy: 0.8429
Epoch 99/100
- 2s - loss: 0.0821 - accuracy: 0.8934 - val_loss: 0.1168 - val_accuracy: 0.8357
Epoch 100/100
- 2s - loss: 0.0376 - accuracy: 0.9513 - val_loss: 0.0460 - val_accuracy: 0.9429
* Accuracy on training set: 97.89%
* Accuracy on test set: 94.29%
这时候准确率大大的提高了。。
预测代码:
def predict(model_path, image_path1, image_path2, target_size):
saved_model = load_model(model_path, custom_objects={'contrastive_loss': contrastive_loss})
image1 = cv2.imread(image_path1)
image2 = cv2.imread(image_path2)
# 灰度化,并调整尺寸
image1 = cv2.cvtColor(image1, cv2.COLOR_BGR2GRAY)
image1 = cv2.resize(image1, target_size)
image2 = cv2.cvtColor(image2, cv2.COLOR_BGR2GRAY)
image2 = cv2.resize(image2, target_size) # <class 'numpy.ndarray'>
# print(image2.shape) # (80, 80)
# print(image2)
# 对图像数据做scale操作
data1 = np.array([image1], dtype='float') / 255.0 / 255.0
data2 = np.array([image2], dtype='float') / 255.0 / 255.0
print(data1.shape, data2.shape) # (1, 80, 80) (1, 80, 80)
pairs = np.array([data1, data2])
print(pairs.shape) # (2, 80, 80)
y_pred = saved_model.predict([data1, data2])
print(y_pred)
# print(y_pred) # [[4.1023154]]
# pred = y_pred.ravel() < 0.5
# print(pred) # 如果没有 <0.5则为 [4.1023154] 有的话则是 [False]
# y_true = [1] # 1表示两个是一个类,0表示不同的类
# if pred == y_true:
# print("是同一类")
# else:
# print("不是同一类")
我们再使用保存的模型来预测,效果大致上是不错的,但是还是会有误识别。可能我的想法还是有点问题。。。。这个我会再学习。
PS:这篇博文主要是自己学习Siamese Network 做的笔记,参考各路大神的笔记,整理于此,然后自己实践。
参考文献:https://www.zhihu.com/search?type=content&q=%E5%AD%AA%E7%94%9F%E7%BD%91%E7%BB%9C%E7%9A%84%E5%8E%9F%E7%90%86
https://blog.csdn.net/weixin_45250844/article/details/102765678?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-4&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-4
https://blog.csdn.net/bestrivern/article/details/88605384?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-2&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-2
https://zhuanlan.zhihu.com/p/29058453
https://github.com/keras-team/keras/blob/master/examples/mnist_siamese.py
关于mnist 数据集训练Siamese Network的地址:http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf
https://sorenbouma.github.io/blog/oneshot/
https://zhuanlan.zhihu.com/p/35040994
https://blog.csdn.net/autocyz/article/details/53149760
不经一番彻骨寒 怎得梅花扑鼻香
 2,孪生神经网络的疑问及用途
2,孪生神经网络的疑问及用途