还是数学建模中的一个小问题,具体概念分析在百度上的大佬说的已经足够详细,在此不再赘述。
链接:
多元回归分析
.
我主要根据实例讲解如何通过spss进行建模,并进行模型参数的分析和验证。
打开spss(如果遇到打不开的情况,可能是由于SPSS加载excel表格时,如果excel表格中的数字没有设置保留位数,就会自动在各位四舍五入。在excel中预先设置小数位数,然后用SPSS加载即可。),点击【分析】——【回归】——【线性】

依次设置因变量,自变量,个案标签(即为序号),方法设为【逐步】。

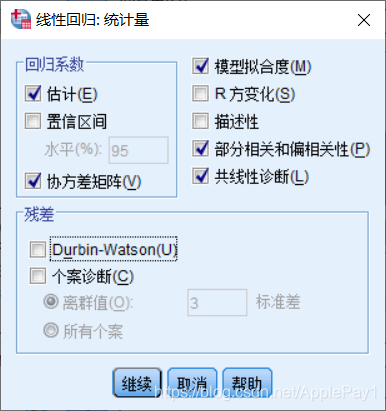
点击【统计量】,勾选图表如下,具体作用后文中将详述。
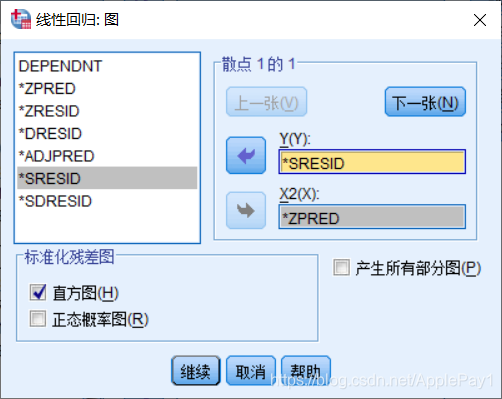
依次分别点击【绘制】和【选项】,操作如下。
最后,点击【确定】,开始建模,结果图如下。
1、首先采用逐步选择法根据设置的移入移出概率筛选自变量。
2、再用R的平方判断变异性能,例如自变量流速,r2=0.262,表明室外温度的变异中有26.2%是由变量流速Xn的变异引起的。所以,r2叫判定系数。
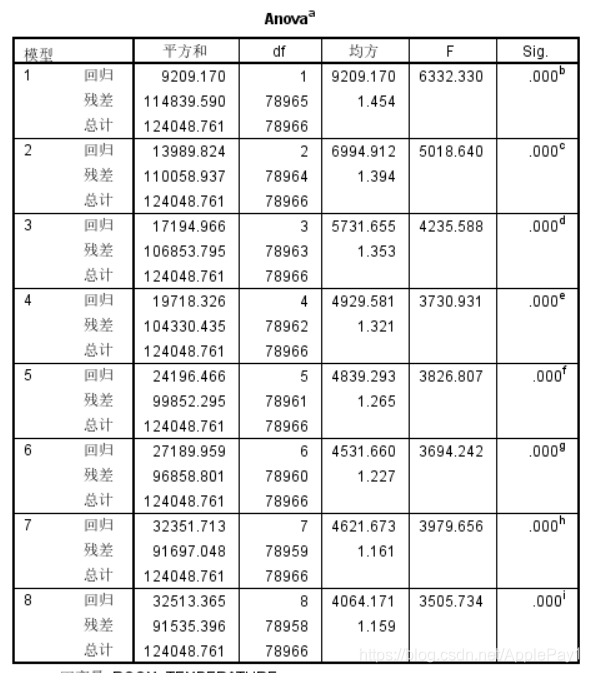
3、观察sig值判断显著性,若sig值近似为零则可以判断显著,一般采用的是小于0.05,即置信区间是95%,如图所示,sig值完全满足要求,模型显著性强。
4、根据系数矩阵中的值判定模型的系数,此处我采用的是模型8。
5、由残差直方图可知残差完美符合正态分布
至此建模结束。
有问题的同学可以私聊我或者在评论区留言。
还是数学建模中的一个小问题,具体概念分析在百度上已经有了足够详细的描述,在此不再赘述。我主要根据实例讲解如何通过spss进行建模,并进行模型参数的分析和验证。链接: 多元回归分析....
一、实际应用
回归分析方法理论成熟,它可以确定变量之间的定量关系并进行相应的预测,反映统计变量之间的数量变化规律,为研究者准确把握自变量对因变量的影响程度和方向提供有效的方法,在经济、金融和社会科学方面具有广泛的应用。
回归分析研究分析某一变量受其他变量影响的分析方法,它以被影响变量为因变量,以影响变量为自变量,研究因变量与自变量之间的因果关系,包括简单线性回归、多重线性回归、
2,在【字段】中选择使用预定角色;
3,在【
模型
】中按需求选择建模方法;
注:当
模型
不再将新字段纳入
模型
,也不再将已有字段移出
模型
时,完成回归
模型
的建立。建模时,纳入F概率<移除F概率,纳入F值>移除F值。
4,在【专家】中,一般...
1.【分析】【回归】【多项logistic】,打开主面板—— 因变量、自变量分别按照箭头指示移入对应的变量框内,点击【参考类别】按钮,默认勾选【最后一个类别】。(指以因变量和自变量的最后一个分类水平为参照,用其他分类依次与之对比,考察不同水平间的倾向。)
2.主面板中,点击【
模型
】,打开【多项logistic回归:
模型
】对话框,勾
数据分析
记录(六)–多元线性回归在
SPSS
中的实现(步骤及指标含义)
本文仅作为自己的学习记录以备以后复习查阅
在回归分析中,如果有两个或两个以上的自变量,就称为多元回归。事实上,一种现象常常是与多个因素相联系的,由多个自变量的最优组合共同来预测或估计因变量,比只用一个自变量进行预测或估计更有效,更符合实际。因此多元线性回归比一元线性回归的实用意义更大。
以上这段解释来自百度百科,我觉得解释的已经比较清楚了,就直接这样放上来,下面放一下
SPSS
进行多元线性回归的步骤。
一 明确自变量和因变量
多元线性回归的
1、 在回归分析中,回归系数的显著性检验通常采用的统计量是 F。 ( 错 )
回归方程通常是F检验 回归系数是T检验
2、 多元线性回归数学
模型
为 。 (对)
3、 回归系数显著性检验时通常采用的统计量是F。 ( 错 )
4、 回归方程显著性检验时通常采用的统计量是 F。 ( 对 )
5、t 检验用于检验回归方程中各个参数的显著性。 ( 错 )
6、F 检验用于检验整个回归关系的显著性。 ( 对 )
整个回归关系指的就是整个方程
7、 各解释变量合起来对被解释变量有显著的线性关系,并不意味着每一个解释变量对被解释
变量有显著线性关系。 ( 对 )
共线性的另一种解释,也
SPSS
(Statistical Package for the Social Sciences)是一种统计软件,常用于社会科学研究中的
数据分析
和统计建模。
多元回归分析
是其中的一种常见方法,用于研究多个自变量对一个因变量的影响。
以下是一个
多元回归分析
案例数据的示例:
假设我们想研究某个公司员工的工资与其学历、工作经验和性别之间的关系。我们收集了该公司不同员工的工资、学历、工作经验和性别等数据。
使用
SPSS
进行
多元回归分析
,首先我们需要导入数据。在
SPSS
中,我们可以将工资作为因变量,而学历、工作经验和性别作为自变量。然后,我们将运行
多元回归分析
模型
,来探索自变量与因变量之间的关系。
在分析过程中,我们可以观察到每个自变量对工资的影响。例如,通过分析结果,我们可以得出结论:学历对工资有显著的正向影响,即具备更高学历的员工往往获得更高的工资;工作经验对工资也有正向影响,即工作经验越丰富的员工往往获得更高的工资;性别可能对工资没有显著的影响,即男性和女性在工资上没有明显差异。
通过
SPSS
多元回归分析
,我们可以进行统计推断并得出关于各个自变量对因变量的影响程度的结论。这些结论可以帮助我们更好地理解变量之间的关系,并为公司制定薪酬政策、员工培训等提供依据。
总之,
SPSS
多元回归分析
可以帮助我们揭示变量之间的关系,为研究和决策提供有益的信息。