1. 第一次扫描数据集或者是数据库，导出频繁项（一项集）的集合，并统计出各自的支持度计数（频度），按照支持度计数，将所有的一项集从大到小排列成一个结果集L。
2. 第二次扫描数据集或者是数据库，将每个事务中的项都按照L中的次序排列。
3. 针对于每个频繁项，构造它的条件模式基，然后再构造它的条件FP-树。
4. 在新构造的条件FP-树上重复上一过程，直到结果条件FP-树为空，或者它只包含一条路径（单个路径将产生其子路径的所有组合，每个子路径是一个频繁模式）

如下图的数据表单L1，该数据库有9个事务，第一列为购买Id，第二列为购买的物品。
最小支持度计数：2。

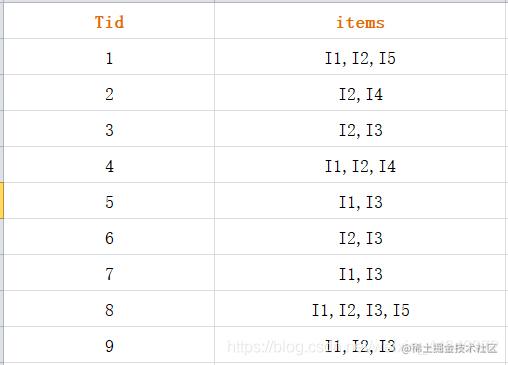
▲第一步，扫描数据库，得出结果集L：{ { I2 : 7 } , { I1 : 6 } , { I3 : 6 } , { I4 : 2 } , { I5 : 1 } ,}
其中，{ I2 : 7 } 表示 I2 出现 7次。
因此我们得出一个顺序：②①③④⑤。
▲第二步，再次扫描数据库，将items里面的事务按照上一步的顺序进行排列，得出以下表L2:

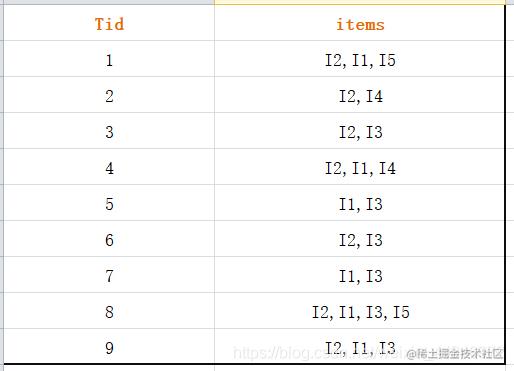
▲第三步，接下来我们开始构造每个单项集的 条件模式基 （一个“子数据库”，由FP树中与该后缀模式一起出现的前缀路径集组成）。

• 我们从支持度最小的 I5 开始：

  我们在L2表中寻找以 I5 为后缀的项集：{I2 , I1 , I5} ，{I2 , I1 , I3 , I5}
  去掉后缀I5，得出 I5 的 条件模式基 {I2 , I1} ，{I2 , I1 , I3 } ——> {I2 , I1 :1} ，{I2 , I1 , I3 :1} ，后面的1代表计数，意思就是两者均出现一次。
  然后我们根据{I2 , I1 :1} ，{I2 , I1 , I3 :1}构造 条件FP树 。
  第一次{I2 , I1 :1} 创建节点I2，I1并计数，第二次延续节点I2，I1并创建节点I3，计数。

因为I3支持度计数是1，小于最小支持度计数2，故将I3去掉，剩下I2和I1。
该分支是以I5为后缀，并且该分支为单路径，所以该单个路径产生频繁模式的所有组合是：
{I2，I5：2}、{I1，I5：2}、{I2，I1，I5：2}。
根据上述步骤我们可以找到 I4 的频繁项集： {I2，I4：2} 。
以上I5和I4这种单个路径的可以依据这个过程求出频繁项集，如果遇到多个路径呢？我们来看一下I3：
首先还是找出I3的条件模式基：寻找以I3为后缀的项集并计数，得出{I2，I1：2}、{I2：2}、{I1：2}。
然后构造条件FP树，如下图

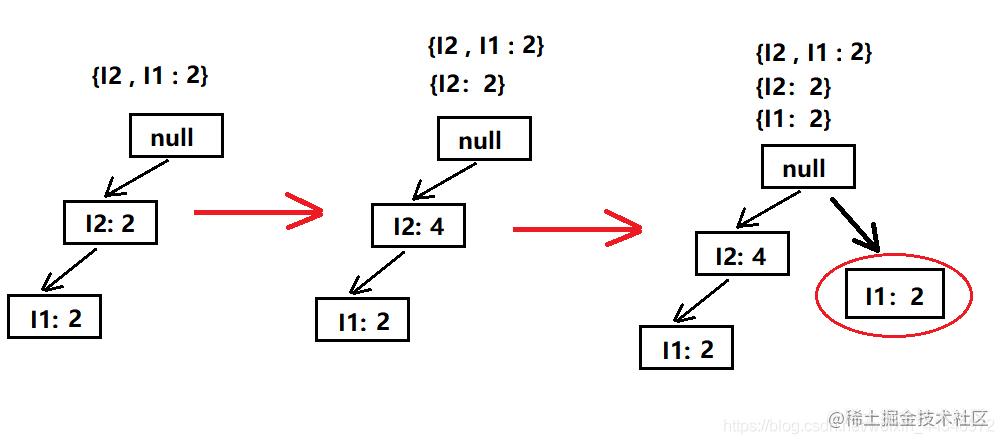
当添加{I1：2}项的时候由于没有I2为前缀，所以产生了分支。
这下该怎么找频繁项集呢？不急，按照前面的模式我们先把当前的频繁项集找出来：I2出现了四次，I1也出现了四次（两个I1相加），因为我们是以I3为后缀的，所以得出频繁项集：
{I2，I3：4}、{I1，I3：4}。
此时频繁项集还没有找完，因为是多分支，所以我们需要将树往上“推”，原先我们的后缀是I3，这个时候我们要再增加一个树中最底层的I1，也就是把{I1，I3}当作后缀，此时右边的分支就“推”没了，左边的分支只剩下I2，原来的两条路径变成了单个路径，所以得出频繁项集：{I2，I1，I3：2}。
这个时候 以I3为后缀 的所有频繁项集我们就都找出来了：{I2，I3：4}、{I1，I3：4}、{I2，I1，I3：2}。

• 最后，I1产生的频繁项集是{I2，I1：4}，由于数据中没有以I2为后缀的项集，故I2没有产生频繁项集。

文中侧重于算法的理解，并无代码实现，还望小伙伴们多多包涵！