度量学习中的pair-based loss
度量学习
度量学习(Metric Learning)是一种空间映射的方法,其能够学习到一种特征(Embedding)空间,在此空间中,所有的数据都被转换成一个特征向量,并且相似样本的特征向量之间距离小,不相似样本的特征向量之间距离大,从而对数据进行区分 。度量学习应用在很多领域中,比如图像检索,人脸识别,目标跟踪等等。
在深度学习中,很多度量学习的方法都是 使用成对成对的样本进行loss计算的,这类方法被称为 pair-based deep metric learning 。例如,在训练模型的过程,我们随意的选取两个样本,使用模型提取特征,并计算他们特征之间的距离。 如果这两个样本属于同一个类别,那我们希望他们之间的距离应该尽量的小,甚至为0;如果这两个样本属于不同的类别,那我们希望他们之间的距离应该尽量的大,甚至是无穷大。正是根据这一原则,衍生出了许多不同类型的pair-based loss,使用这些loss对样本对之间的距离进行计算,并根据生成的loss使用各种优化方法对模型进行更新。本文将介绍一些常见的pair-based metric learning loss。
Contrastive los
Contrastive loss [1] 是最简单最直观的一种pair-based deep metric learning loss,其思想就是:
1) 选取一对样本对,如果其是正样本对,则其产生的loss就应该等于其特征之间的距离(例如L2 loss);因为我们的期望是他们之间的距离为0,所以凡是大于零的loss都需要被保留。
2) 如果是负样本对,他们之间的距离应该尽可能的大,至于应该大到多少则由我们人为的设定,假设设定的阈值为 m ,如果距离大于 m ,则说明模型已经不错了,不需要对模型进行更新了,如果小于 m ,则认为模型还不够好,需要继续训练。
根据这一思想, 可以得到如下形式的Contrastive Loss:
\mathcal{L} \left( \left \lbrace D_{i j} \right \rbrace \right)=\sum_{y_{i j}=1} D_{i j}+\sum_{y_{i j}=0}\left[m-D_{i j}\right]_{+}
上式中 D_{ij} 代表样本 i 和 j 之间的距离 , y_{ij} = 1 代表这两个样本属于同一个类别,是一对正样本对; y{ij} = 0 代表这两个样本属于不同类别,是一对负样本对。 []_+ 是hinge 函数: [x]_+ = max(0, x) 。
如上式,如果是正样本对,其产生的loss就等于两个样本之间的距离,这里的距离函数一般取L2距离。如果是负样本对,当两个样本之间的距离大 m 时,其loss为0,在模型更新的时候,loss为0,意味着不对模型进行更新。
Contrastive loss能够让正样本对尽可能的近,负样本对尽可能的远,这样可以增大类间差异,减小类内差异。 但是其需要指定一个固定的margin,即公式中的 m ,因为 m 是固定的,所以这里就隐含了一个很强的假设,即每个类目的样本分布都是相同的,不过一般情况下这个强假设未必成立 。
例如,有一个数据集有三种动物,分别是狗、狼 、猫,直观上狗和狼比较像,狗和猫的差异比较大,所以狗狼之间的margin应该小于狗猫之间的margin,但是Contrastive loss使用的是固定的margin,如果margin设定的比较大,模型可能无法很好的区分狗和狼,而margin设定的比较小的话,可能又无法很好的区分狗和猫。
Triplet loss
Constrastive Loss的思想是让正样本对之间的距离尽可能的小,负样本对之间的距离尽可能的大。从而达到增大类间差异,减小类内差。在训练的过程中选取的要么是正样本对,要么是负样本对。
Triplet Loss [2] 的思想是让负样本对之间的距离大于正样本对之间的距离,在训练过的过程中同时选取一对正样本对和负样本对,且正负样本对中有一个样本是相同的。仍旧以前面的狗、狼、猫数据为例,首先随机选取一个样本,此样本称之为anchor 样本,假设此样本类别为狗,然后选取一个与anchor样本同类别的样本(另一个狗狗),称之为positive,并让其与anchor样本组成一个正样本对(anchor-positive);再选取一个与anchor不同类别的样本(猫),称之为negative,让其与anchor样本组成一个负样本对(anchor-negative)。这样一共选取了三个样本,即triplet。
其loss形式如下:
\mathcal{L} \left( \left \lbrace D_{i j}\right \rbrace \right) =\sum_{(i,j,k), \atop y_{ij}=1, y_{ik}=0} \left[D_{ij}-D_{ik}+m\right]_+
通过上述公式可以看出,当负样本对之间的距离比正样本对之间的距离大m的时候,loss为0 ,认为当前模型已经学的不错了,所以不对模型进行更新。
Triplet Loss最先被用于人脸识别中,如下图,输入一个triplet对(三张图像),使用同一个网络对这个三张图像进行特征提取,得到三个embedding向量,三个向量输入到Triplet Loss中得到loss,然后根据loss值使用反向传播算法对模型进行更新。
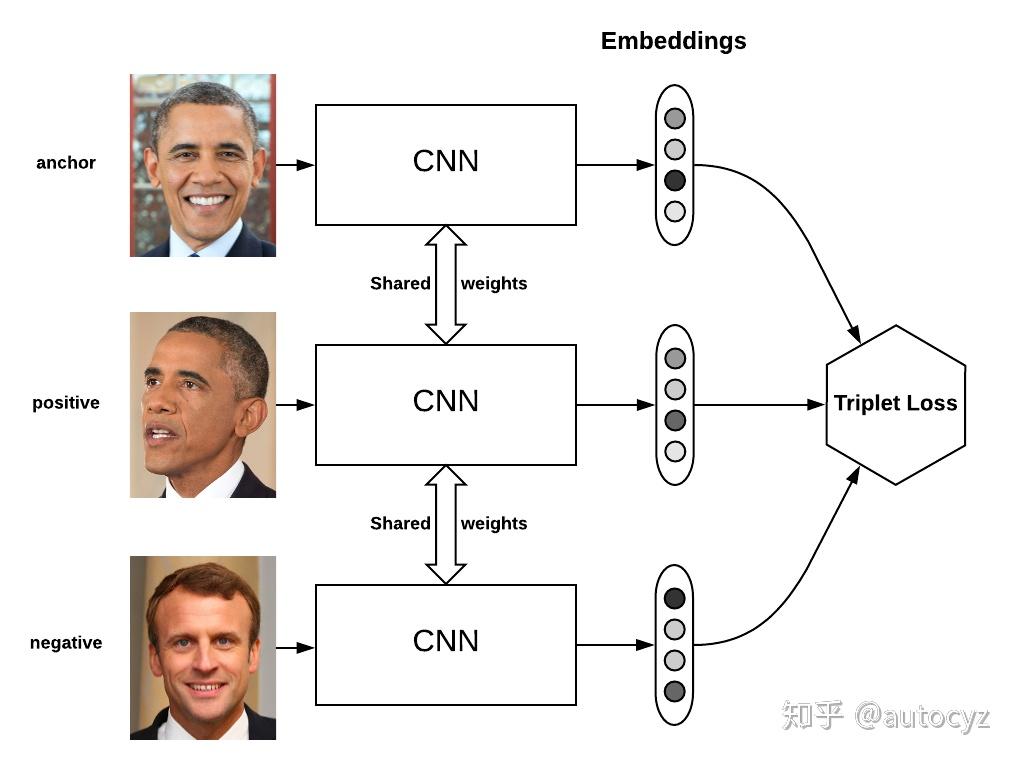
Triplet center loss
Triplet Loss是让正样本对之间的距离小于负样本对之间的距离,并且存在一定的margin。因此triplet样本的选取至关重要,如果选取的triplet对没啥难度,很容就能进行区分,那大部分的时间生成的loss都为0,模型不更新,而如果使用hard mining的方法对难例进行挖掘,又会导致模型对噪声极为敏感。为了对Triplet loss的缺点进行改进,Triplet center loss就被提出来了。
Triplet Center loss [3] 的思想非常简单,原来的Triplet是计算anchor到正负样本之间的距离,现在Triplet Center是计算anchor到正负样本所在类别的中心的距离。类别中心就是该类别所有样本embedding向量的中心。

Triplet Center Loss形式如下:
\mathcal{L}\left(\left\lbrace D\right\rbrace\right)=\sum\left[D_{ap_c}-D_{an_c}+m\right]_+ $$
其中 D_{ap_c} 表示的是anchor样本到正样本类别中心的距离, D_{an_c} 表示的是anchor样本到负样本类别中心的距离。
N-pair loss
triplet loss同时拉近一对正样本和一对负样本,这就导致在选取样本对的时候,当前样本对只能够关注一对负样本对,而缺失了对其他类别样本的区分能力。
为了改善这种情况,N-pair loss [4] 就选取了多个负样本对,即一对正样本对,选取其他所有不同类别的样本作为负样本与其组合得到负样本对。如果数据集中有 N 个类别,则每个正样本对 y_{ii} 都对应了 N-1 个负样本对。

N-pair loss的形式如下:
\mathcal{L} \left( \left \lbrace D_{i k} \right \rbrace \right)=\sum_{y_{i i} =1} \log \left(1+\sum_{y_{i k}=0} \exp \left(D_{i i}-D_{i k}\right)\right)
其中 \left \lbrace D_{i k} | i, k=1, \cdots, N ; y_{i i}=1 ; \text { and } y_{i k}=0, \text { if } k \neq i \right \rbrace
Quadruplet loss
Quadruplet loss [5] 由两部分组成:
一部分就是正常的triplet loss,这部分loss能够让模型区分出正样本对和负样本对之间的相对距离。
另一部分是正样本对和其他任意负样本对之前的相对距离。这一部分约束可以理解成最小的类间距离都要大于类内距离,不管这些样本对是否有同样的anchor。即不仅要要求 A_1A_2 < A_1B_1 ,还需要 A_1A_2 < B_1C_1
Quadruplet loss的形式如下:
\mathcal{L} \left( \left \lbrace D_{i j}\right \rbrace \right) =\sum_{(i,j,k), \atop y_{ij}=1, y_{ik}=0} \left (\left[D_{ij}-D_{ik}+m\right]_+ + \sum _{y _{k_aak_b} = 0} \left[ D_{ij} - D_{k_ak_b} + m\right] _+\right)
Lifted Structure Loss
Lifted Structure loss [6] 的思想是对于一对正样本对而言,不去区分这个样本对中谁是anchor,谁是positive,而是让这个正样本对中的每个样本与其他所有负样本的距离都大于给定的阈值。此方法能够充分的利用mini-batch中的所有样本,挖掘出所有的样本对。
\mathcal{L} \left( \left\lbrace D_{i j} \right \rbrace \right) = \sum_{y_{i j}=1} \left[D_{i j} + \log \left( \sum_{y_{ik} = 0} \exp(m - D_{ik})\right) + \log \left( \sum_{y_{jl} = 0} \exp(m - D_{jl}) \right) \right]_{+}
总结
度量学习中还有很多其他类型的pair-based loss,通过上文可以发现,这些不同的loss基本上都是在Contrastive loss和Triplet loss的基础上改进而来。这些改进思想很值得我们借鉴,尤其是通过观察分析已经存在的loss的缺陷,从而提出针对性的改进,构造一个适合自己应用场景的loss。
参考
- ^ Dimensionality Reduction by Learning an Invariant Mapping http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf
- ^ FaceNet: A Unified Embedding for Face Recognition and Clustering https://arxiv.org/abs/1503.03832
- ^ Triplet-Center Loss for Multi-View 3D Object Retrieval https://arxiv.org/abs/1803.06189
- ^ Improved Deep Metric Learning with Multi-class N-pair Loss Objective http://www.nec-labs.com/uploads/images/Department-Images/MediaAnalytics/papers/nips16_npairmetriclearning.pdf
- ^ Beyond triplet loss: a deep quadruplet network for person re-identification https://arxiv.org/abs/1704.01719
- ^ Deep Metric Learning via Lifted Structured Feature Embedding https://arxiv.org/abs/1511.06452


