感知机,又来一个线性分类器!(二)
线性回归?逻辑斯蒂回归?不再让你傻傻分不清!(一) 这篇文章中,我们学到了一个二分类的分类器 —— Logistic Regression,实际上它是一个对数线性分类器,广义上讲,也属于线性分类器的范畴。我们借由sigmoid函数“映射”,解决了非正态分布的棘手问题,使得可以利用较为熟悉的线性回归的“套路”来解决,同时因为这种“映射”转换,模型假设输出的结果不再是一个拟合的实际数值,而是相对的概率,然后以0.5的概率阈值进行二分类的划分。模型的学习过程,就是确定模型参数的过程,我们定义了损失函数,利用梯度下降的方法,不断迭代参数,最终实现损失函数最小化,此时获得最终的模型参数,模型也就确定下来了。
感知机
其实还有一种简单的二分类的线性分类模型,叫 感知机 (perceptron)。与逻辑斯蒂回归从概率的角度判别不同,感知机可以理解为从几何的角度上做判断,即求得一个分离超平面,可以将对应输入空间中的实例划分为正负两类。感知机模型简单,理解也容易,实际生活中直接应用较少,但却是神经网络和支持向量机的基础,所以还是要掌握扎实的。
李航老师的《统计学习方法》一书中,用线性方程 w\cdot x + b = 0 定义 超平面 S ,其中 w 是超平面的 法向量 , b 是超平面的 截距 ,这个超平面将特征空间划分为两个部分,位于两部分的点被分为正、负两类,如图
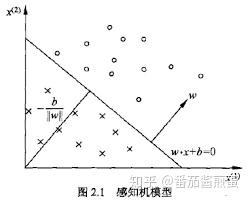
超平面与法向量
看到这里,反正我是一头雾水了,凭什么可以这样定义平面呢?为什么 w 是超平面S的法向量呢?来证明一下!
证明:
有超平面 w\cdot x + b = 0 ,设超平面上任意两点 x_1,x_2 , 它们满足:
\left\{\begin{matrix} w\cdot x_1 + b = 0 & (1)\\ w\cdot x_2 + b = 0&(2) \end{matrix}\right.
(1) - (2) 得
w\cdot (x_1-x_2) = 0
因为 x_1 - x_2 = \overrightarrow{x_2x_1} ,所以 w\cdot \overrightarrow{x_2x_1}= 0 ,即 w 与 \overrightarrow{x_2x_1} 垂直。
超平面上的其他点也类似 x_1,x_2 , w 垂直于平面上的任意直线,所以 w 是超平面 S 的法向量。
其实,上面的不过是初高中的数学内容,时间久没接触,忘了,捡起来就好!
感知机函数
与Logistic Regression里面正负类分别用1和0表示不同,感知机中约定俗成的正负类分别用+1和-1表示。我们希望正实例点完全正确的划分到超平面正类聚集的一侧,也就是 w\cdot x + b > 0 时,输出+1; w\cdot x + b < 0 ,输出-1
我们想到能做到这一点的就是符号函数啦, sign(x) = \left\{\begin{matrix} +1, & x\geqslant0\\ -1, &x<0 \end{matrix}\right.
将 w\cdot x+b 作为输入就得到感知机函数 f(x) = sign(w\cdot x+b) ,模型学习的过程还是确定 w 和 b 的过程。
无论是Linear Regression还是Logistic Regression,模型学习的过程中,我们都有定义损失函数,然后以损失函数最小化为目标,梯度下降迭代确定模型的最终参数。如同之前我们碰到的损失函数都是衡量预测值与真实值“差距”的Mean Square Error,感知机的损失函数也有类似的定义,它的 损失函数是误分类点到超平面 S 的总距离 (为什么不用误分类点的个数?因为没法优化啊!)就是正确的点我不管你离超平面有多远,分对了正负类就行,在感知机中不太“在意”正确分类点距离超平面的距离,但在其他,比如支持向量机中,这个距离是需要“重视”的,也是衡量模型“好坏”的标准之一。
点到平面的距离
损失函数是误分类点到超平面的总距离,就是各个误分类点分别到超平面的距离之和,这涉及到点到平面距离的知识了,又要回顾一下基础的数学知识了~
- 平面一般式方程: Ax + By + Cz + D = 0 ,其中 \overrightarrow{n} = (A,B,C) 是平面法向量(上面我们已经简单证明过), D 是将平面移动到坐标原点所需距离( D = 0 时平面过原点)
- 向量 \overrightarrow{v} = (x,y,z) 的模: \left| \overrightarrow{x} \right| = \sqrt{x^2 + y^2 + z^2}
- 向量 \overrightarrow{v_1} = (x_1,y_1,z_1) 和向量 \overrightarrow{v_2} = (x_2,y_2,z_2) 内积(点积): \overrightarrow{v_1}\cdot \overrightarrow{v_2} = x_1x_2 + y_1y_2 + z_1z_2
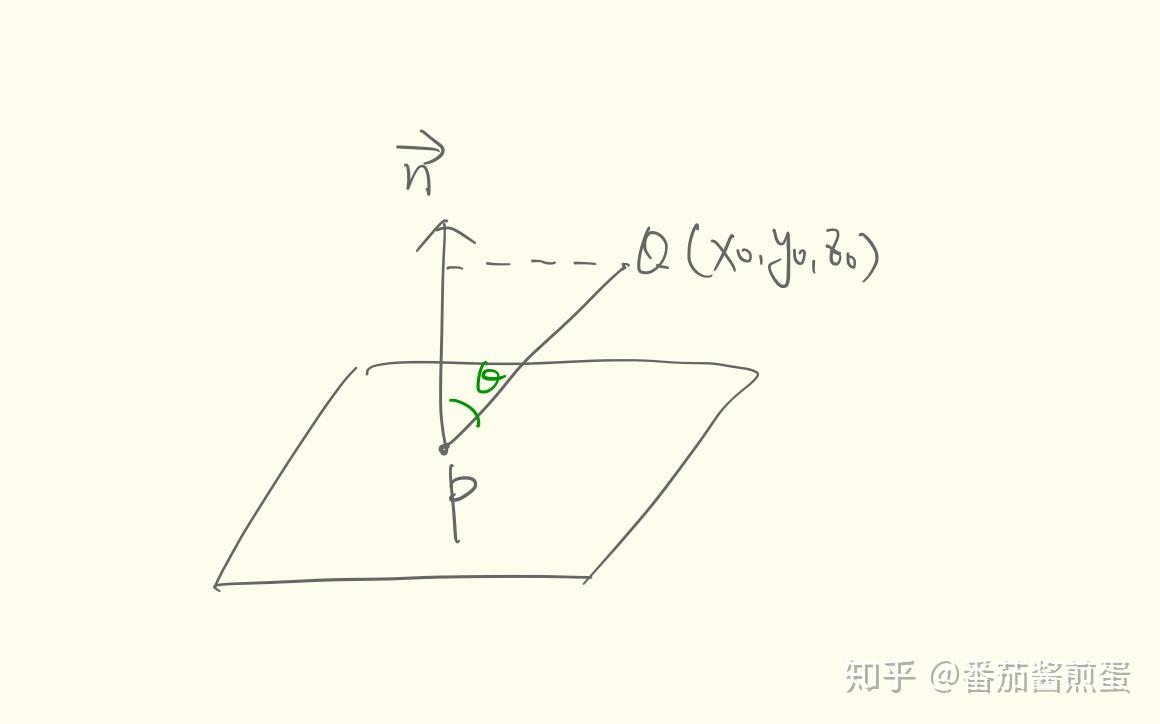
如图,求给定平面 Ax + By + Cz + D = 0 外点 Q(x_0,y_0,z_0) 到平面距离 d :取平面内一点 P(x,y,z) , Q 到平面的距离恰是 \overrightarrow{PQ} 在法向量 \overrightarrow{n} 上投影的长度 d = \left| \overrightarrow{PQ}\right|\cdot cos \theta = \frac{\left| \overrightarrow{n}\right|}{\left|\overrightarrow{n} \right|}\cdot \left| \overrightarrow{PQ}\right|\cdot cos \theta = \frac{\overrightarrow{PQ} \cdot \overrightarrow{n}}{\left|\overrightarrow{n} \right|}
= \frac{A(x_0-x) + B(y_0-y) + C(z_0-z)}{\sqrt{A^2+B^2+C^2}}
=\frac{Ax_0+By_0+Cz_0-(Ax+By+Cz)}{\sqrt{A^2+B^2+C^2}}
由 Ax + By + Cz + D = 0 得 Ax + By + Cz = -D
于是,上式 =\frac{Ax_0+By_0+Cz_0+D}{\sqrt{A^2+B^2+C^2}} ,为保证距离为正值,加绝对值符号
d=\frac{\left| Ax_0+By_0+Cz_0+D\right|}{\sqrt{A^2+B^2+C^2}}
感知机的损失函数
上面的结论带到我们超平面的定义中,点 (x_i,y_i) 到超平面的距离为
d = \frac{1}{\left \| w\right \|}\left|w\cdot x_i + b\right| ,其中 \left \| w\right \| 为向量 w 的 L_2 范数,公式里就是 w 的模呀
求总距离之前我们需要去掉绝对值符号,分情况讨论。
误分类点有两种情况,就是负类分成了正类( w\cdot x_i + b < 0 , y_i = +1 )和正类分成了负类( w\cdot x_i + b > 0 , y_i = -1 ),总是异号的,所以距离可以改写为 d = -\frac{1}{\left \| w\right \|}y_i(w\cdot x_i + b) ,
于是误分类点到平面的总距离可以表示为 -\frac{1}{\left \| w\right \|}\sum_{x_i \in M}{y_i(w\cdot x_i + b)} ,其中 M 为误分类点的集合,
不考虑系数 \frac{1}{\left \| w\right \|} ,得到 感知机的损失函数 L(w,b) = -\sum_{x_i \in M}{y_i(w\cdot x_i + b)}
感知机的学习
与之前Linear Regression和Logistic Regression相同,模型的学习问题可转化为损失函数最小化的问题,即目标是 minL(w,b) = -\sum_{x_i \in M}{y_i(w\cdot x_i + b)}
对 w 的偏导: \frac{\partial}{\partial w}L(w,b) = -\sum_{x_i \in M}{y_ix_i}
对 b 的偏导: \frac{\partial}{\partial w}L(w,b) = -\sum_{x_i \in M}{y_i}
随机 选取一个误分类点 (x_i,y_i) ,对 w,b 进行更新
w:=w-(-\eta y_ix_i) = w+\eta y_ix_i
b:=b-(-\eta y_i) = b+\eta y_i
其中 \eta (0\leqslant \eta \leqslant1) 是“步长”,又称为学习速率。这样通过迭代,可以期待损失函数不断减小直到为0。之所以可以为0,是因为感知机是线性分类器,输入数据集为线性可分数据集,就是无论步骤多少、速度快慢,我们最终总能“全部分对”。
感知机算法的原始形式
输入 :线性可分数据集 T = \{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} ,其中 x_i\in X = R^n, y_i\in \{-1,+1\} , i = 1,2,...,N , 学习速率 \eta (0\leqslant \eta \leqslant1)
输出 : w,b 感知机模型 f(x) = sign(w\cdot x+b)
1、选取初值 w_0,b_0
2、在训练集中选取数据 (x_i,y_i) ( 注意是任意选取的,而且选取不同,后面结果不同 )
3、如果 y_i(w\cdot x_i + b)\leqslant 0
迭代 w,b w:=w+\eta y_ix_i
b:=b+\eta y_i
4、转至步骤2,直到训练集中没有误分类点为止。
算法的直观解释 :当一个实例点被误分类,即位于分离超平面的错误一侧时,则调整 w,b 的值,使分离超平面向该误分类点的一侧移动,以减少该误分类点与超平面间的距离,直至超平面越过该误分类点使其被正确分类。(这个过程,我称为“点不动面动”)
向量角度画图解释 :

李航老师的《统计学习方法》中例2.1可以自己手算一下,过一遍算法的步骤,而且可以发现最开始随机选择不同的误分类点,最终得到的感知机模型不同,但都能够正确划分,不分好坏,这里不再赘述。
感知机的对偶形式
其实感知机的对偶形式没有什么特别的,原理相同,但是算法改进,速度得到提升。思路就是将 感知机原始形式中 w,b 的一步步迭代判断“集成”一部分到矩阵运算中 ,从而加快计算,在对大数据集训练模型的时候,加快模型学习的速度。
还是这样的迭代: w:= w+\eta y_ix_i
b:=b+\eta y_i
逐步修改 w,b ,设修改 n 次,则 w,b 关于 (x_i,y_i) 的增量分别是 \eta n_iy_ix_i 和 \eta n_iy_i 令 \alpha_i = \eta n_i ,最终学习到的 w,b 就可以分别表示为
w = \sum_{i=1}^{N}\alpha_iy_ix_i
b = \sum_{i=1}^{N}\alpha_iy_i
其实就是将迭代 w,b 转化成迭代 \alpha,b ,具体怎么提升速度的,我们后面讲
感知机算法的对偶形式
输入 :线性可分数据集 T = \{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} ,其中 x_i\in X = R^n, y_i\in \{-1,+1\} , i = 1,2,...,N , 学习速率 \eta (0\leqslant \eta \leqslant1)
输出 : \alpha,b 。 感知机模型 f(x) = sign(\sum_{j=1}^{N}\alpha_jy_jx_j\cdot x + b)
其中 \alpha = (\alpha_1,\alpha_2,...,\alpha_N)^T
1、选取初值 \alpha=0,b=0
2、在训练集中选取数据 (x_i,y_i)
3、如果 y_i(\sum_{j=1}^{N}\alpha_jy_jx_j\cdot x_i + b) \leqslant 0
迭代 \alpha_i := \alpha_i + \eta
b := b+\eta y_i
4、转至步骤2,直到训练集中没有误分类点为止。
观察步骤3中,训练实例以 内积 的形式出现 x_j\cdot x_i ,我们可以预先将训练集中实例间的内积计算出来并以矩阵的形式存储,这个就是所谓的 Gram矩阵
G = [x_j\cdot x_i]_{N\times N}
放到例2.1中就是
\begin{bmatrix} x_1\cdot x_1 &x_1\cdot x_2 &x_1\cdot x_3 \\ x_2\cdot x_1 &x_2\cdot x_2 &x_2\cdot x_3\\ x_3\cdot x_1&x_3\cdot x_2 & x_3\cdot x_3 \end{bmatrix}
这下明白什么意思了吧~ 由于这种矩阵“操作”,迭代次数大大减小了
总结
感知机学习算法是基于随机梯度下降法的对损失函数的最优化算法,有原始形式和对偶形式,算法简单易于实现。原始形式中,首先任意选取一个超平面,然后用梯度下降法不断极小化目标函数,在这个过程中一次随机选取一个误分类点使其梯度下降。对偶形式提前计算了实例内积并存储在矩阵中,将参数迭代部分转换为“更新次数”迭代,大大减少了梯度下降迭代次数,使得模型的学习速度得到提升。

