因果推断在度小满金融场景的应用探索
导读: 本文将从因果推断的一些核心概念入手,介绍因果推断与传统机器学习技术的差异,因果推断适合去解决哪些问题,以及因果推断在实际业务中的应用。
文章将分为三大部分:
- 什么是因果推断
- 为什么使用因果推断
- 因果推断的实战应用
分享嘉宾|李东晨 度小满数据智能应用部 资深算法工程师
编辑整理|韩筱 北京航空航天大学
出品社区|DataFun
01/什么是因果推断

首先介绍一个关键概念: 因果关系和相关关系的区别 。
在工作和生活中,人们习惯用协方差来表达两个变量之间的相关关系。如右图,红线代表每年在游泳池的溺水人数,黑线代表影星尼古拉斯·凯奇每年参演电影的数量,从协方差视角来看,这两个变量是强相关的。但是当两个变量强相关的时候,是否对于目标优化产生价值?例如,目标是降低每年在游泳池的溺水人数,而控制尼古拉斯凯奇每年参演的电影数量对此意义不大。
因此,在决策中不希望得到与结果强相关的变量,我们希望找到一种变量:在保持其他条件不变的情况下,对这个变量进行改变,目标值也能随之发生改变。这样的变量才是可以支持决策的变量,才是与目标具有因果关系的变量。比如在经济学领域,物品价格的降低一定会引起物品的交易量的提升,价格和交易量是具有强因果关系的变量。
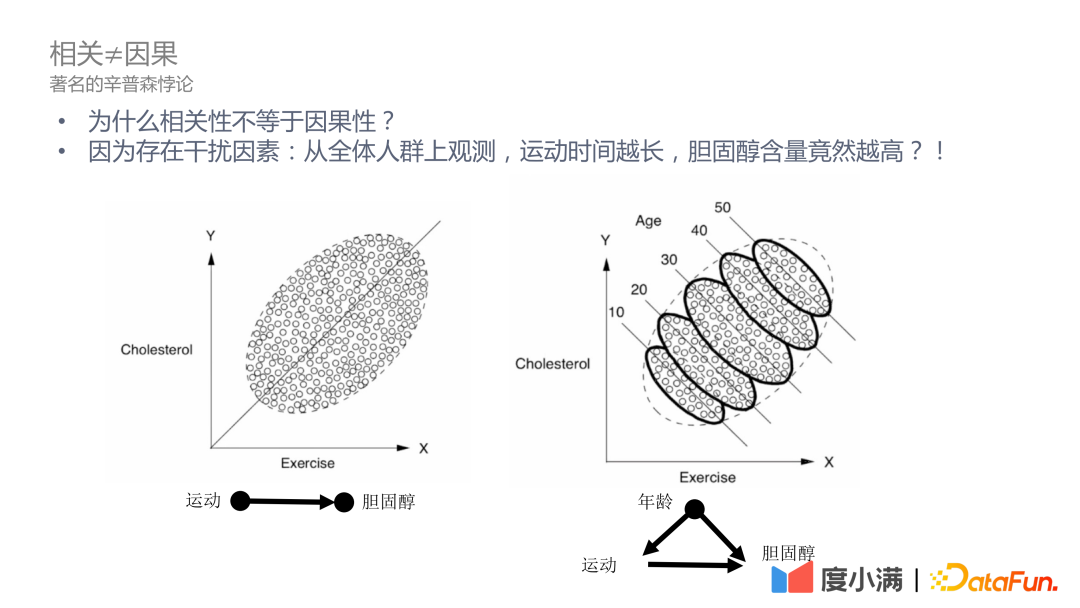
上图解释了相关和因果的关系 。左图从整体人口的角度去观测,随着运动量提升,人体内的胆固醇增加,显然违背常识,原因是观测数据中存在干扰因子。在这个例子中年龄是干扰因子。当我们对年龄进行控制,在不同的年龄分段,人的胆固醇的含量会随着运动的增加而减少,符合我们的认知事实。
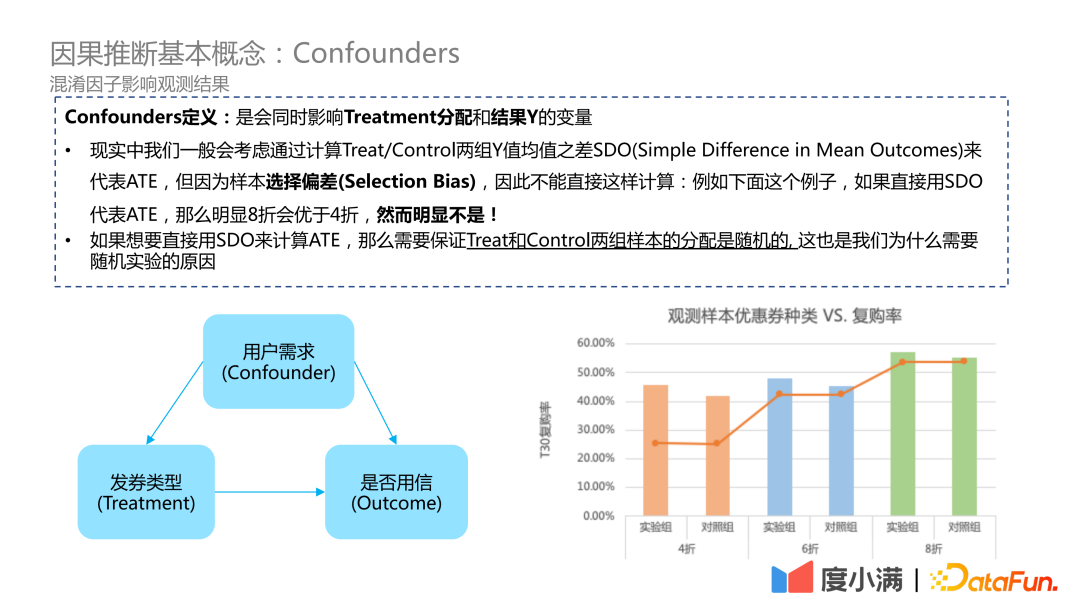
由此引出了因果推断中另一个关键的概念: 混淆因子(Confounders) 。定义为:会同时影响 Treatment 分配和结果 Y 的变量。在实际的线上 A/B 实验中,我们经常会将实验组和对照组结果均值的差异作为实验效果的评估。但是线上实验并不完全随机,而是具有倾向性。
在实际的业务中,假如需要提升整体用户的复购情况,我们会人为地干扰实验的分配:可能会对活跃度较低的用户发放更高的权益,对活跃的用户发放较低的权益。在观测的数据上就会出现权益越好,复购率越低的现象,原因是观测数据中存在干扰因素:用户需求。如果想要用组间Y的均值差异计算群体的因果效应,我们需要确保实验的分配是随机的。
--
02/为什么使用因果推断
接下来介绍一下因果推断在社会科学领域解决的问题。

首先在医学领域 ,存在的问题是:不同用户对药剂的敏感程度不同,如何给用户搭配最合适的服药剂量,达到治愈率最大。解决方法是:做临床控制变量实验:对相似的患者提供不同的药剂,观测两组用户的群体治疗结果,即典型的群体因果效应预估问题。
在经济领域 ,2021 年诺贝尔经济学的问题是:从观测的数据分析教育时长与收入的关系。经济学领域较难做类似医学领域的临床实验,而受教育程度往往跟人本身的年龄和智商有关,因此在观测数据中无法直接证明教育时长与收入有因果关系。解决方法是:找到一组年龄和用户资质水平都近似的样本,这两组样本在其他特征相似的情况下,仅教育时长改变,之后观测两组样本的群体收入差异,即典型的因果关系分析问题。
度小满对两种问题都有所实践。第一个问题是 :不同用户对于不同权益(优惠券)的敏感程度不同,如何在控制成本的情况下,给用户搭配最适合的权益,达到效率最高的目标。与医学领域不同,我们希望因果效应能够预估到个体,即个体因果效应预估。 第二个问题是 :需要从观测样本中分析某些变量是否与结果具有因果关系,即改变了这个变量,是否能改变业务结果?

上面的这些例子反映了 目前主流的因果推断的框架 :
- 第一类是因果效应预估,即预估施加了干预后的效果。但一个用户在同一时间内仅能观测到一种干预下的效果,需要通过潜在输出框架(Potential Outcome Model)预估反事实效果。
- 第二类是因果关系分析,希望借助 SCM 框架(Structure Causal Model),通过观测数据中发现变量间的因果关系。
为什么要使用因果推断技术呢?传统机器学习存在哪些局限性?
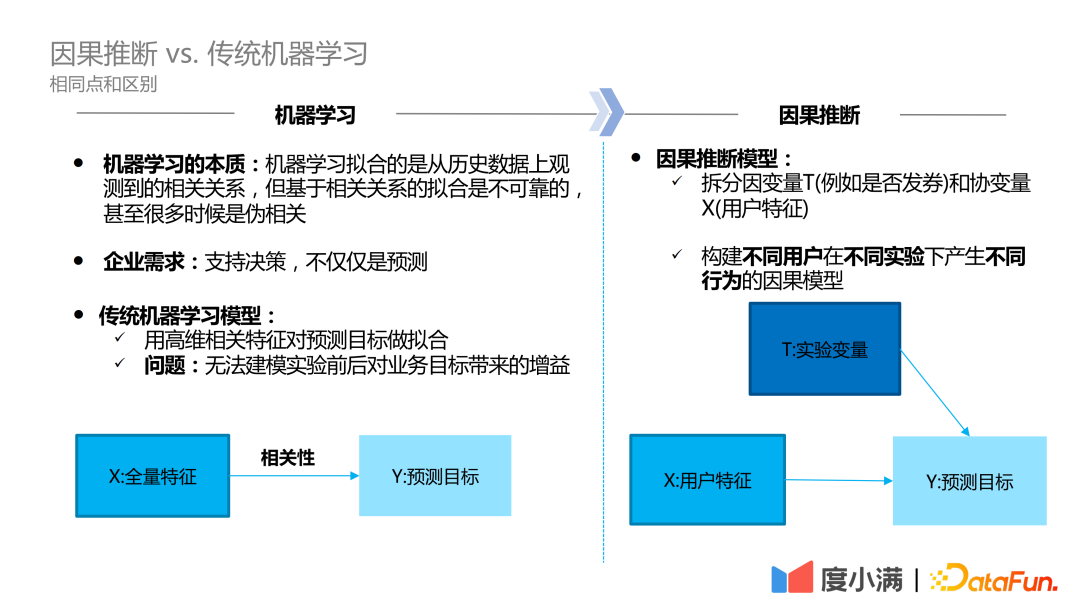
从上图可以看出,传统的机器学习是预测工作,即拟合用户的高维特征与 Y 值之间的相关性,但是相关性有时不能支持决策。因果推断是先拆分因变量 T(例如是否发券)和协变量 X(用户特征),然后构建不同用户在不同实验下产生不同行为的因果模型。
可以更加形式化地去表达机器学习和因果学习之间的差异。
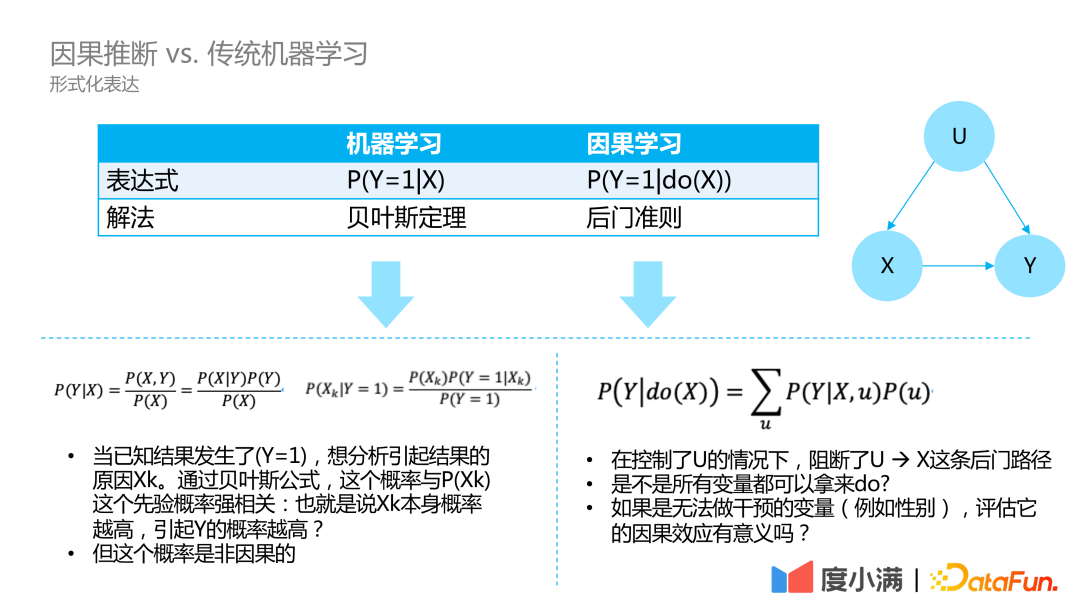
机器学习是一个条件概率,需要去预估在X的情况下 Y=1 的概率,因果学习需要写成 do 算子的形式。do 算子指的是需要预估 X 取不同值的情况下 Y 的差异。
传统机器学习采用贝叶斯定理进行求解 ,而右图反应了一个典型的因果学习,U 是混杂因子 Confounder,U 既会影响 X 的分布,也会影响结果 Y 的分布。因为 U 到 X 之间后门路径的存在,导致观测数据不能体现出正常的因果关系。
因果推断是如何求解的呢? 这是一个形式化的表达,与 Exercise 和体内胆固醇含量的例子相同,需要对 Confounders 进行控制,即分层:在每个分层下做条件概率的预估,最后写成求和形式。在后门准则调整了 Confounders 的情况下,才能正确的对 X 对 Y 的因果效应去做一个正确的预估。
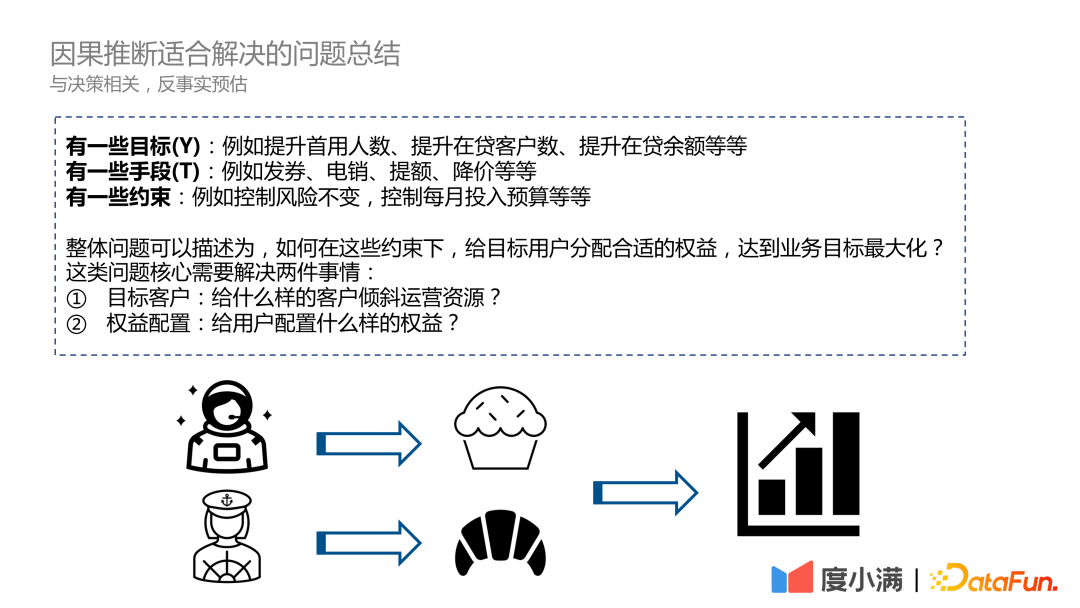
再来总结一下 因果推断适合解决的问题:
- 有一些目标:比如业务目标是提升首用人数,提升在贷客户数,提升在贷余额等。
- 有一些手段:为了达成这些目标,有一些手段,比如对用户做营销的发券,对用户做电销的推广,提额,降价等等。
- 有一些约束:手段存在一些约束,比如金融领域控制风险,预算的限制。
问题可以描述为:在这些约束的情况下,如何给目标客户分配合适的权益,从而达到业务目标最大化。
这类问题核心是两件事情,第一个事情是确定我的目标客户,选择什么样的客户倾斜运营资源;第二个事情是在已知客户情况下,如何给客户分配权益,从而在约束下,达到业务目标最大化。
接下来结合度小满实战的应用案例,来阐释因果推断适合解决什么样的问题。
--
03/因果推断的实战应用
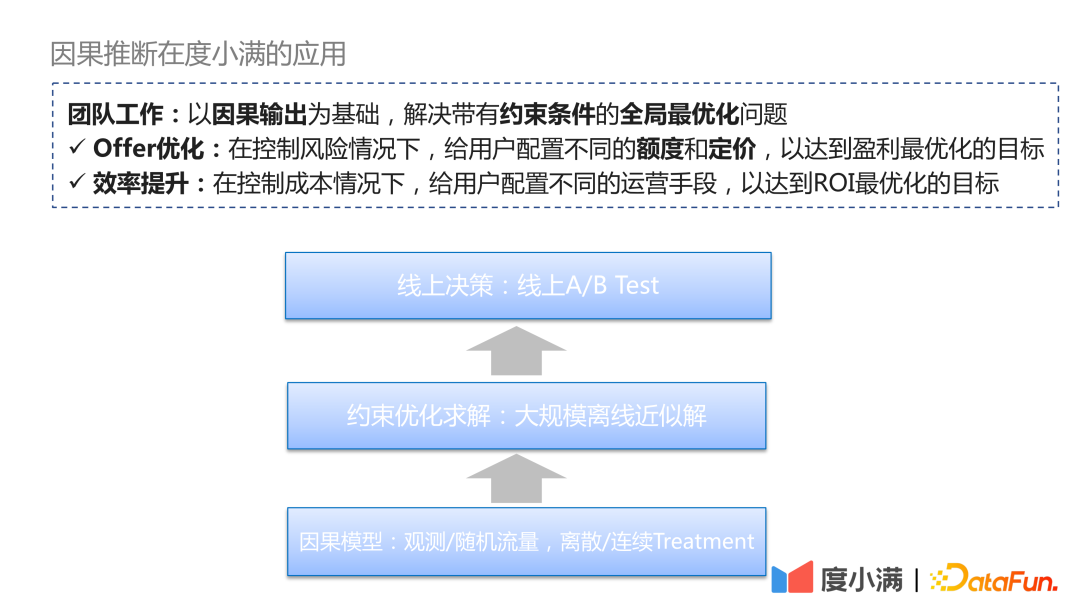
我们的工作是以因果输出作为基础,解决带有约束条件的全局最优化问题。在金融领域有两个比较重要的应用场景:
- 第一个场景是通过因果推断做 Offer 优化。Offer 会影响到用户风险的变化,在 Offer 优化场景下,我们希望在控制风险的前提下,给用户配置不同的额度和定价,从而达到盈利最优。
- 第二个场景是存在一些运营的手段,在控制成本的情况下,给用户配置不同的运营手段,从而达到 ROI 最大化。
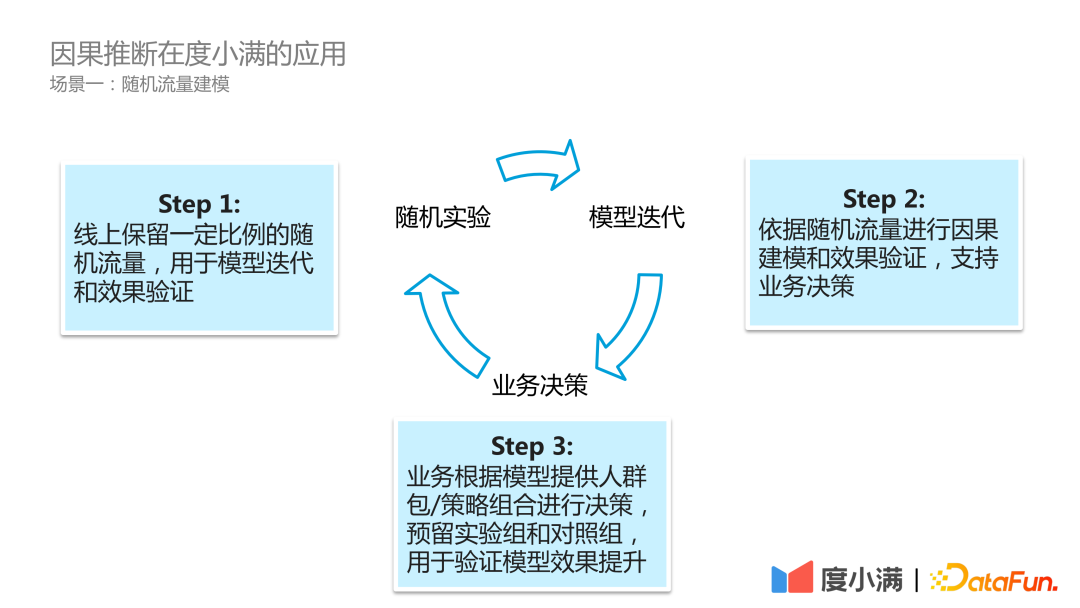
接下来介绍 度小满关于上述两个典型问题的因果推断建模方式 。
首先是一个比较理想的建模方式:
第一步在线上去保留一定比例的随机流量,随机流量可以用于模型的迭代和模型效果的验证。
第二步是拥有了一定的随机流量后,可以依赖随机流量去进行因果模型的建模和离线效果的预估,从而支持业务的决策。
第三步就是业务决策,业务根据因果模型和离线求解获得的人群包或策略组合,进行线上真实的业务决策。业务决策需要预留实验组和对照组,通过实验组和对照组观测模型带来怎样的效果提升。这是一个循环的过程,由于随机流量可以一直线上保留,模型可以一直采用随机流量进行效果迭代和更新。
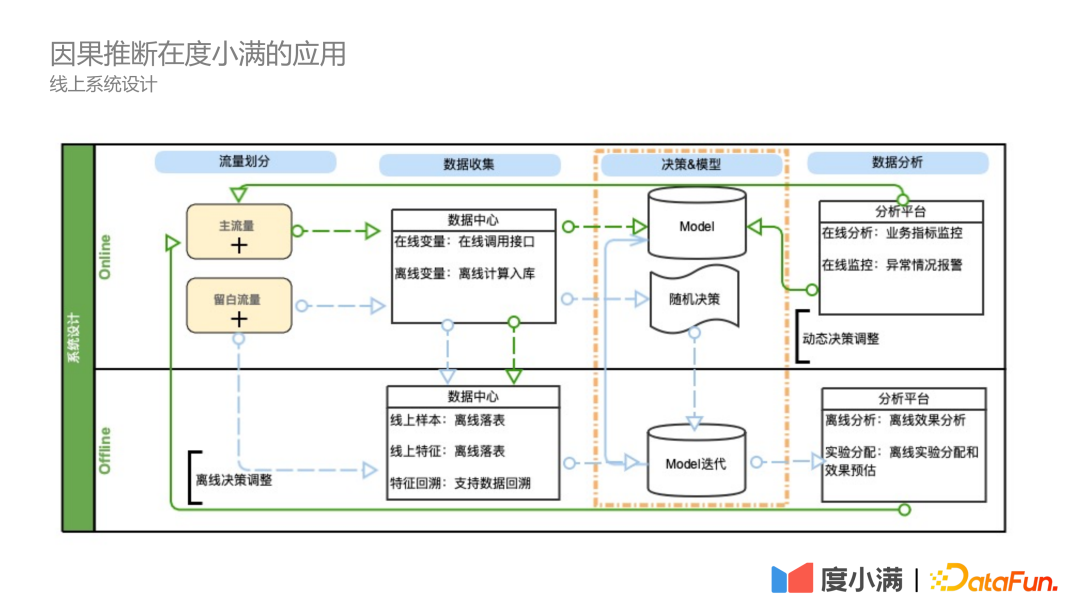
上图表示度小满典型的可支持因果建模和决策的线上系统设计图 。这个因果决策系统分为四个重要部分,依据线上线下,两块具有不同的工作。
- 第一块是流量划分模块。流量划分决定了目前用户是走主流量决策还是主流量对照或者留白流量。
- 第二块是数据中心模块,在线功能是决定实时调用模型决策需要的变量;离线功能是能够进行线上样本和特征的实时落表,以及特征的实时回溯。
- 第三块是决策和模型模块,离线功能是根据线上落表的样本和数据去进行模型的实时迭代;线上功能是部署线下模型进行实时决策。
- 第四块是数据分析平台,在线功能支持线上业务指标的监控,以及业务指标的报警;离线功能支持离线的数据分析以及离线的模型实验分配和效果的预估。
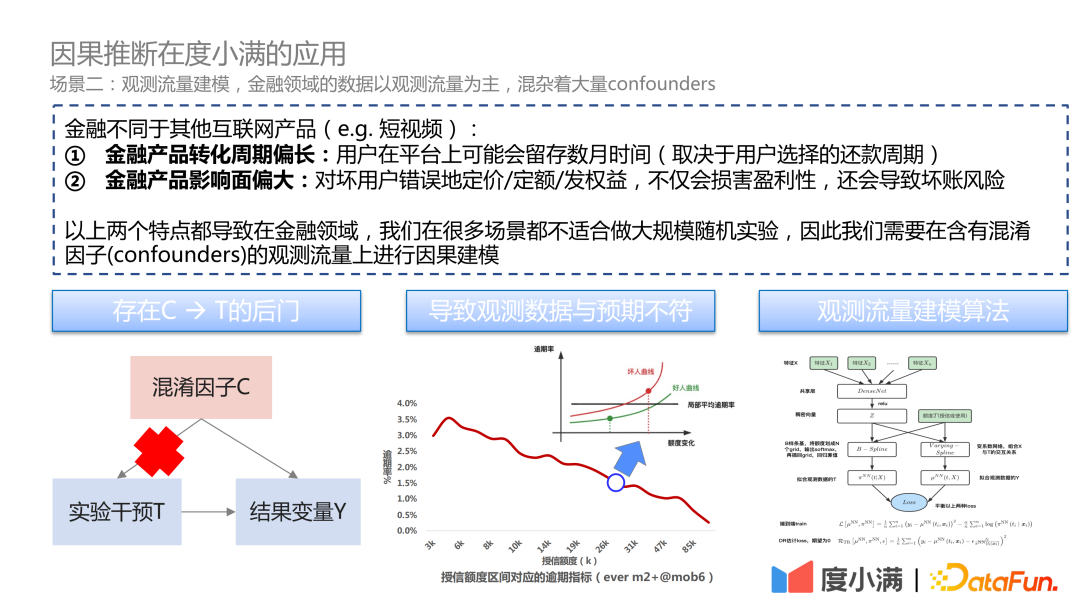
以上是比较理想化的实验设计和分配案例,金融产品特性不同于其他互联网产品,金融产品转化周期偏长,金融平台的用户会留存较长时间,这取决于用户的还款周期。金融产品的影响面也偏大,如果对坏用户进行错误定价、错误定额,或错误发权益,将会损害整体的盈利性,甚至导致坏账风险。
金融产品的两个特点导致金融领域不适合做大规模随机实验。
更多场景是:在含有较多混淆因子的观测流量上进行因果建模。在观测流量上面,因为混淆因子的存在,出现了混淆因子 C 到实验干预 T 的后门,但是我们偏好 C 到 Y 和 T 到 Y 的因果关系。由于后门的存在,在观测流量上观测不到具有因果关系的正常表现。在金融领域,对于好用户,当额度产生变化,好用户逾期的弹性较好;对于坏用户,理想状态将会观测到坏用户的逾期曲线随着额度的变化更加陡峭。
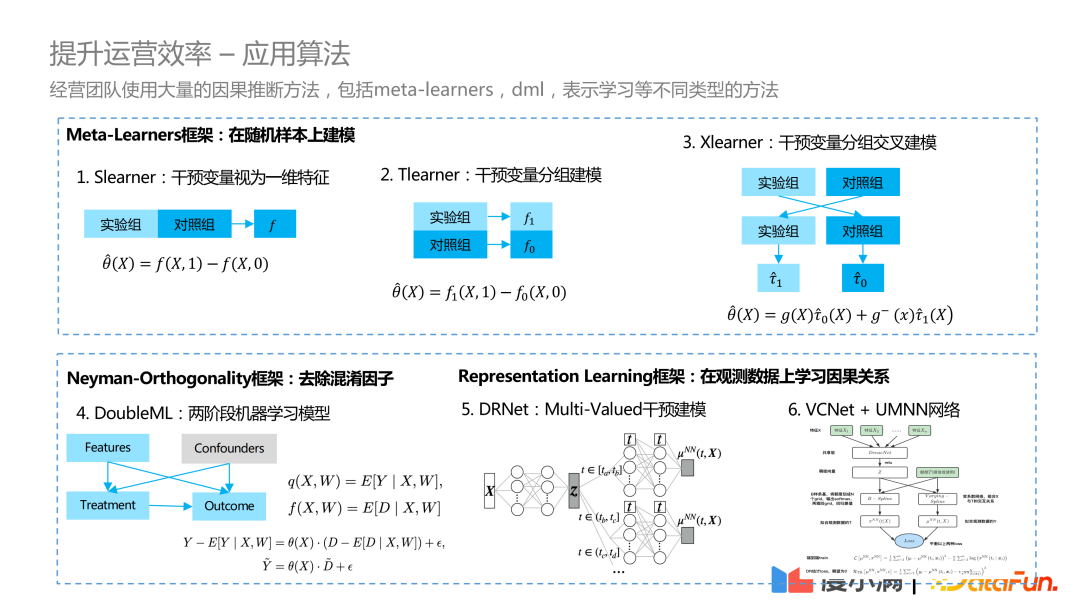
大量的混淆因子观测流量上的建模方式不同于随机实验,我将介绍几个在实战中使用较多的算法框架。度小满进行算法选型时,基本逻辑是考虑样本是否含有随机流量。如果样本是比较好的随机实验,可以用 Meta-Learner 框架解决问题。
Meta-Learner 不是算法而是一种框架,底层算法囊括常见的机器学习算法。首先介绍 T-Learner,它是一种较简单建模评估方式,拆分实验组和对照组去进行单独的拟合建模,因果效应就是两组之间预估的差距。当实验组和对照组的样本的占比差异较大时,T-Learner 具有一定限制。X-Learner 在 T-Learner 上也有所提升,在 X-Learner 中相互介绍对方信息,用对方的信息进行残差拟合,在一定程度上缓解样本不平衡的问题。Meta-Learner 只适合在含有随机流量的样本上进行建模评估。
下面的算法是我们团队常用的一些算法 。首先是 Double-Machine Learning,它是两阶段机器学习的算法。第一阶段用特征和 Confounders 单独对 T 和 Y 进行一阶段预估。在第一阶段预估的基础上,计算 Y 和 \^{Y} 之间的差距以及 T 和 \^{T} 之间的差距。在第二阶段,因果效应可以表达成 ΔT 和 ΔY 之间的参数,或者非参形式,因果效应预估完成。
然后介绍 表示学习框架 。DRNet, 基本思想是 :样本中混淆因子影响 T 的分布,即实验组和对照组的样本特征空间存在差异。那么去寻找无偏的特征空间,在这个特征空间内可以消除 Confounder 产生的 Treatment 差异。
这种是一种比较朴素的想法,我们更多的是关注变量分解的方法,从观测到特征剥离混淆因子、工具变量和协变量,并进行一些表达。
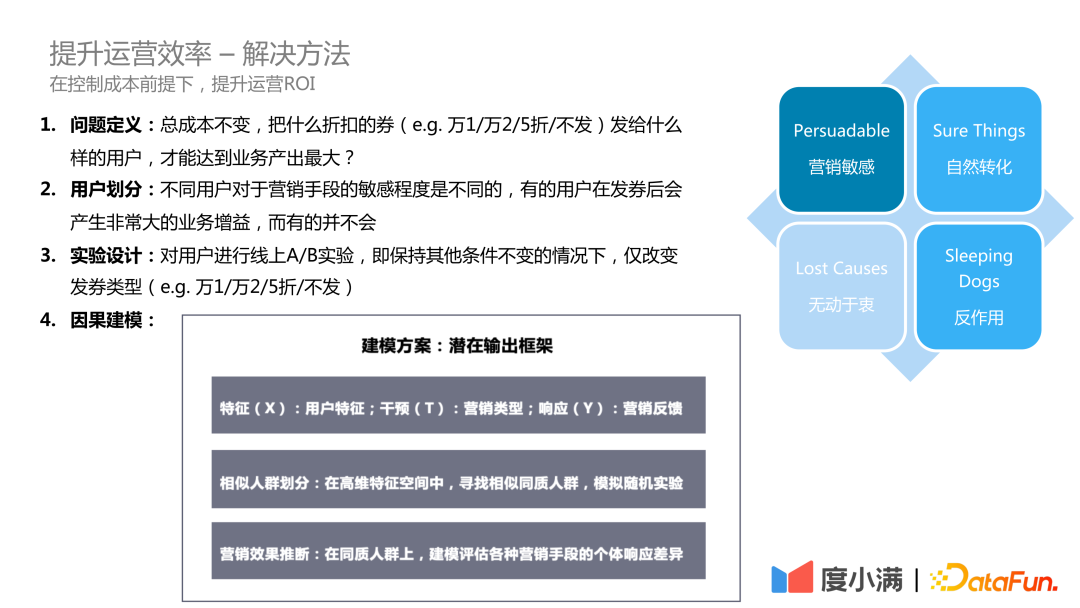
接下来进入 具体的应用案例,需要解决的问题是 :总成本不变,把什么折扣的券(e.g. 万1/万2/5折/不发)发给什么样的用户,达到业务产出最大。
首先进行用户划分,不同用户对于营销手段的敏感程度是不同的,有的用户在发券后会产生较大的业务增益,我希望将资源倾斜给能带来业务增量较大的用户。然后进行实验设计,在理想状态下,对用户进行线上 A/B 实验,即保持其他条件不变的情况下,仅改变发券类型(e.g. 万1/万2/5折/不发)。
在建模中我们使用潜在输出框架,输入是用户的特征 X,干预 T 以及对 T 的反馈 Y。由于社科领域群体的因果效应 ATE 比较粗糙,只对比两个组内差异;个人的因果效应 ITE 很难预估。
目前的工作主要集中于 CATE(Conditional Average Treatment Effect),即在高维的特征空间中对特征进行划分,找到同质的 Subgroups,在 Subgroup 上进行因果效应预估,可以近似代表一类个体的因果效应。

下面介绍一个具体的案例,来阐释因果模型与预测模型之间的差异。如上图,问题是:第一个用户发券带来的增量是 1 万,第二个用户发券带来的增量是 0.5 万,发券后的结果都是 2 万。假设只有一次发券机会,应该将优惠券给谁?
预测模型:只预测收到优惠券后产生的借款。无法区别营销敏感人群和自然转化人群。
因果模型:直接对 Uplift 的增量进行建模,即优惠券而产生的借款,能够精准定位营销敏感人群。

下面我们把上述案例进行形式化的描述。
目标是余额的增量最大化。整体余额增量最大化,可以写为个体增量最大化加和的形式,更具体的,写为个体在不同的 Treatment 下带来的增量形式。增量 ΔTarget 需要依赖第一阶段的 Causal Model 进行预估;第二阶段将根据第一阶段的 Input,以及成本的约束进行离线的整数规划,目标是控制成本最小,即第二阶段给出应该给什么样的人去发什么样的券;第三阶段将策略应用到线上,进行线上的 A/B Test。
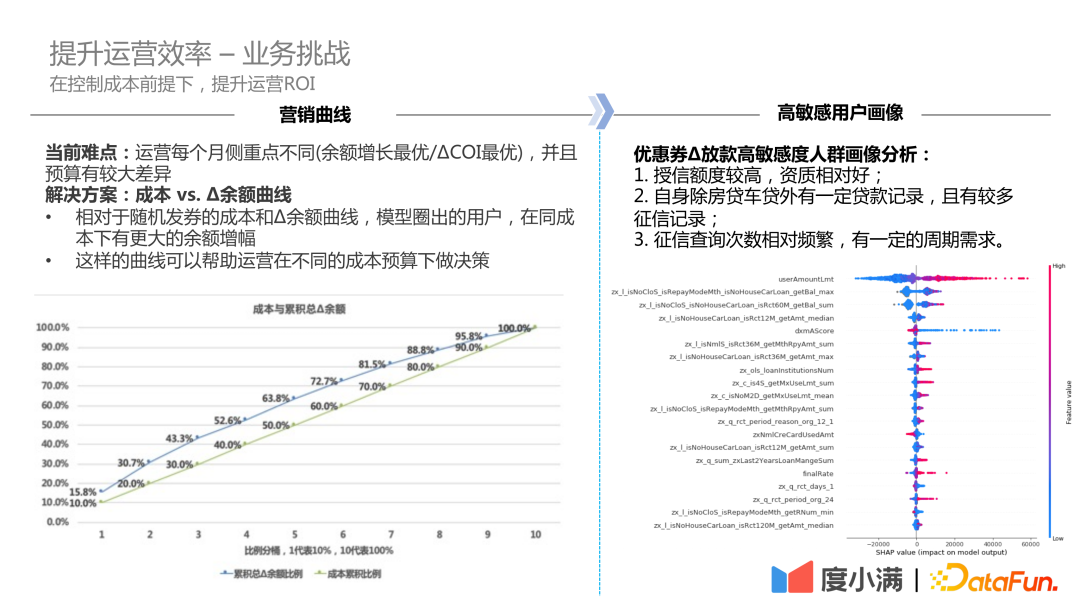
以上是形式化的营销的方法,在实际业务中会有一些具体的问题。
第一个是 每个阶段的侧重点不同(目标可能是余额增长、人头增长、效率最高等等),而且每月之间的预算差异较大。如果根据运营目标调整模型,重新做离线整数规划,那么成本较大。是否有普适化的方式应对这种变化?其实有这样的一种方式。如左下图,绿线代表随机发券方式,发 50% 的券会获得 50% 的业务增量。因果模型把效率更高排在前面,当发同样比例的券可以获得更大的业务增长。当成本发生变化,比如本月只有上月 60% 的预算,但是可以达到比随机大概高 13% 的业务增量。
第二个问题是解释性问题 ,如右图,当给出人群包,目标是分析究竟是什么因素让它用户变得对营销更敏感。关于这个问题,我们对敏感性进行归因。可以发现平台高敏感的用户,本身资质比较好,授信额度比较高,有稳定的外部需求的。对比过其他的用户,有些用户时具有临时需求,具有突增性的一些需求,这时发券会引起较短时间内人头的提升,对长期而言,它还不如有稳定需求的用户。
以上就是度小满应用因果推断进行智能营销的一个具体案例。
下面介绍一些可以 改进的方向 。
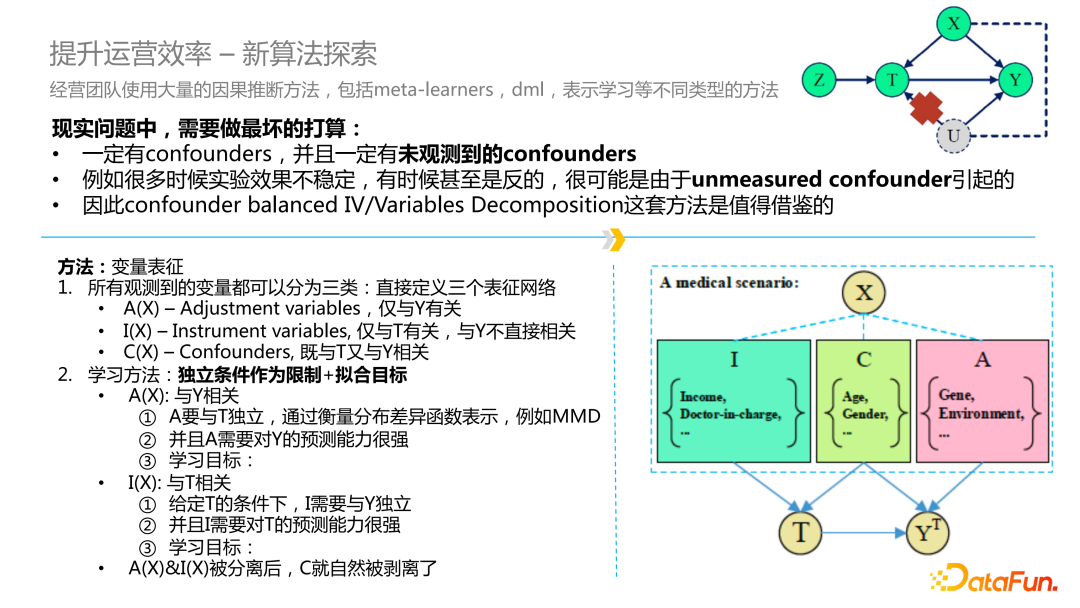
首先,在现实中要做最坏的打算,原因如下:一定有混淆因子,并且一定有未观测到的混淆因子,很多时候实验效果不稳定或者出现反结果,可能是由于未发现的混淆因子引起的。 我们希望借鉴 Confounder Balanced IV/Variables Decomposition 方式对观测到的变量进行拆分。
比如,I 指工具变量,C指混淆因子,I、C 会影响到 T 和 Y 的分布,A 是正常变量可以通过 A、I 的定义去对它们进行特征表示以及神经网络的设计和分离。当拿到 ICA 的分离矩阵之后,可以进一步对 C 和 A 对 Y 和 T 做进一步的预估。这样无需寻找特定的混淆因子,工具变量。虽然没有特定的物理含义表示,但是对于业务的纠偏能力有所提升。
--
04/问答环节
Q1:因果推理是否都需要在对照组中进行干预实验,干预操作是否会影响计算机的自动化处理?
A1:因果推断实际的干预实施在实验组,自动化处理与这个干预没有关系。
Q2:最后一幅图将变量分为 I、C、A 基于什么模型?
A2:这其实是一种表达的方式。比如:把 A 从 X 中剥离需要两个条件,要求A与T独立以及 A 对 Y 有较强的预测能力。那么损失函数是 A 与 T 的 MMD 距离和 A,T 与 Y 之间的交叉熵损失。
Q3:基于历史数据是否可以做高敏感用户画像?与基于 Uplift Model 选出的人群有何差异?
A3:基于历史数据是可以做,但算法选型时要考虑历史的数据是否随机,如果非随机数据,需要通过后门准则调整混杂因子。与 Uplift Model 相比,具体要关注历史数据是如何发放的。
Q4:怎么去做时序方面的一些工作?
A4:这个我们还在探索,可以关注北大苗旺老师的工作。
Q5:因果推断中的因子需要多大程度依赖业务输入?
A5:金融领域的线上实验需要经过业务操作,了解业务选择哪些因素去做的实验控制会极大帮助我们对模型的进行除偏。
今天的分享就到这里,谢谢大家。
分享嘉宾

李东晨|度小满数据智能应用部 资深算法工程师
李东晨,度小满数据智能应用部资深算法工程师,硕士毕业于伦敦大学学院(UCL)计算机系,在互联网金融算法领域深耕6年,当前专注于将因果推断技术与金融业务结合落地。
DataFun新媒体矩阵

关于DataFun
专注于大数据、人工智能技术应用的分享与交流。发起于2017年,在北京、上海、深圳、杭州等城市举办超过100+线下和100+线上沙龙、论坛及峰会,已邀请超过2000位专家和学者参与分享。其公众号 DataFunTalk 累计生产原创文章800+,百万+阅读,15万+精准粉丝。

