Stata是meta分析最常用的软件之一,应用stata做meta分析时,也有很多需要注意的地方,一个小疏忽往往会带来大问题,影响了统计分析的顺利进行。今天给大家总结总结stata操作中的几个常见问题。

1 数据录入问题
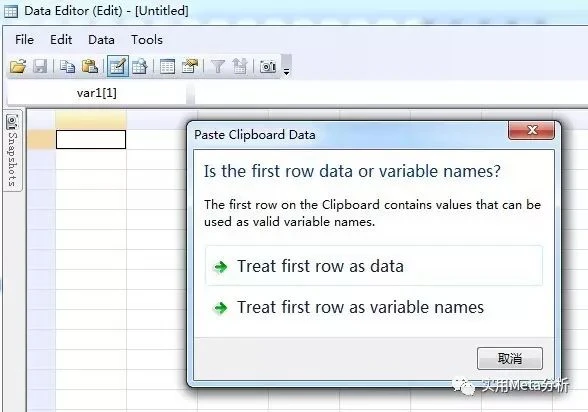
Stata的数据录入,很多时候都是从excel或其它文件中将数据复制,然后粘贴到数据编辑窗口的。此时,stata会有一个弹窗,提示我们:第一行是作为数据还是变量名。
这时候需要根据实际情况选择,复制的时候,第一行是变量名,就需要选择第二项“Treat first row as variable names”;若第一行是数据,则选择“Treat first row as data”,一定不能弄错!
将数据变成了变量名,补救方法就是修改变量名,并重新录入该行数据。
但是,将变量名设置成数据(如图2所示),就不是删除首行,并修改变量名就可以解决的。
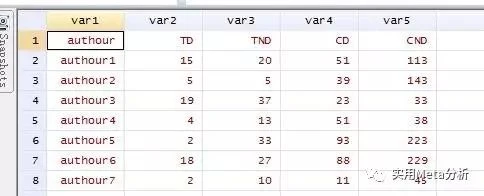
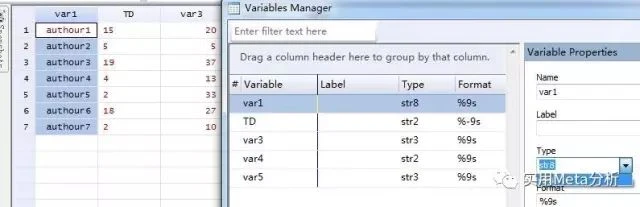
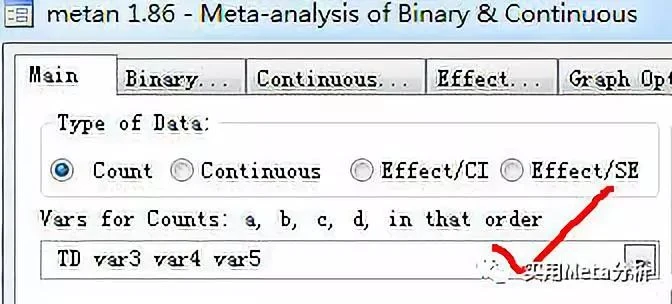
解决方法有两个: 1) 在stata的数据编辑窗口点击:File→New,新建一个空白的数据文件,然后正确录入数据; 2) 通过命令还原数据类型。 如图三所示,删除首行后,TD,var3, var4, var5等数据依然是红色的,而且数据类型不能改变,只能是“str”,也就是string。这类型的数据不能被stata用于统计分析。可以借助命令“destring var, replace”,将其还原为byte格式。然后就可以正常地运行统计分析的操作了。

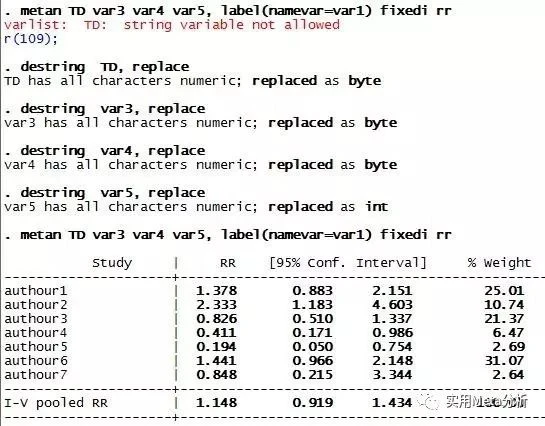
如图5所示,在转换数据类型前,运行“metan”命令做效应值的合并,stata提示数据类型有误“string variable not allowed”,进行数据转换后,meta分析的合并就顺利完成了。
2 Egger或Begg检验运行出错
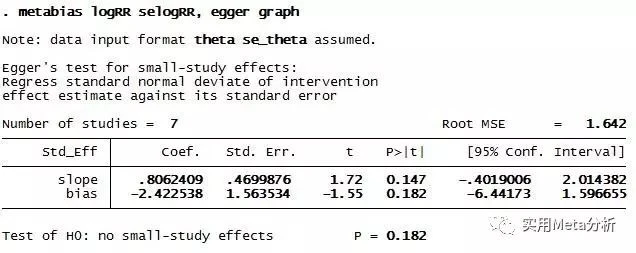
有不少人反映,stata在做Egger、Begg检验的时候报错,命令行:metabias logRR selogRR, graph(egger)运行不了。即便使用菜单操作,也出现同样的问题(图6)。

其实,这是“metabias”的版本升级导致的。“metabias”是Stata完成发表偏倚检验的命令,最早是在1997年编写的,那时候metabias可以做Begg检验和Egger检验,而且只要输入1个命令,Stata就输出2种检验方法的结果。
到了2009年,Harbord对原有的命令进行了修改,增加了两种检验方法:Harbord test和peters test。同时,Egger和Begg检验的命令也有所变化。
此时,Egger检验的命令是怎样的呢?如下图所示,其实命令的变化很小,只是把“graph”放在了最后。
3 效应值没有转换
90%以上的初学者都会犯这个错误,为什么?因为想当然。Stata的一个优点是同时兼容菜单和命令行。有人认为命令行我搞不定,菜单我还不懂吗?然后就开始捣鼓菜单了。 Stata的菜单操作确实很简单,基本上都有说明或操作提示的,按要求操作就行了。可是,你看懂提示了吗? 分类变量要求输入四格表数据,很简单,依次选择试验组的事件发生人数、试验组的事件未发生人数、对照组的事件发生人数、对照组的事件未发生人数。
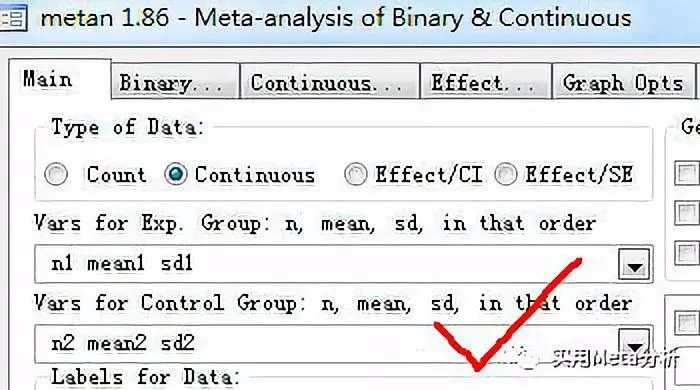
连续资料要求输入两组的“样本量、均数、标准差”,也很简单明了,按顺序选择即可。
效应值的合并,Stata要求输入的是“Effect/CI”,也就是“效应值和95%CI”,下方也有说明:Varsfor Effects: theta, lowerCI, upperCI(效应值、置信区间的下限、上限)。很多人都想当然地以为懂了,于是选择了RR/OR/HR和95%CI(图10)!然而,这里的“theta”是指“logRR”。
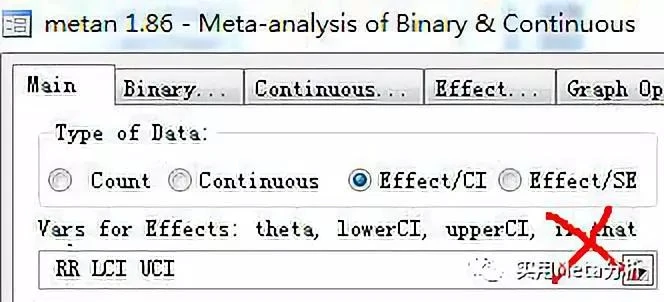
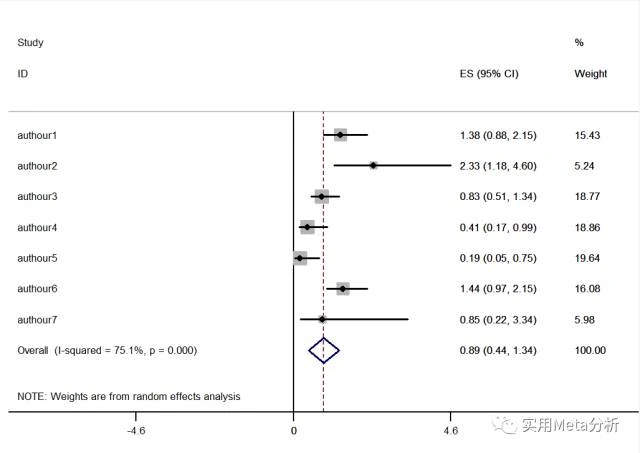
一起来看看用RR和95%CI做出来的结果和森林图吧,合并结果为:0.89 (0.44,1.34),置信区间与1有交集,差异无统计学意义;然而P=0.000<0.05,提示有显著差异。这显然是不对的。
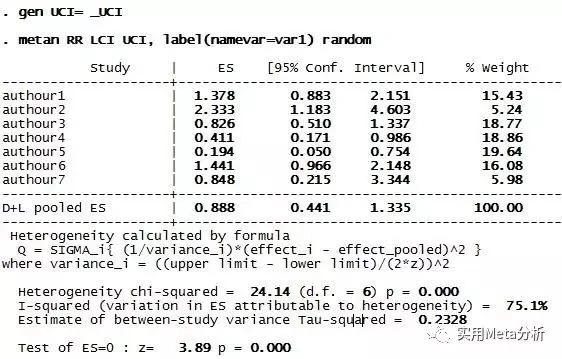
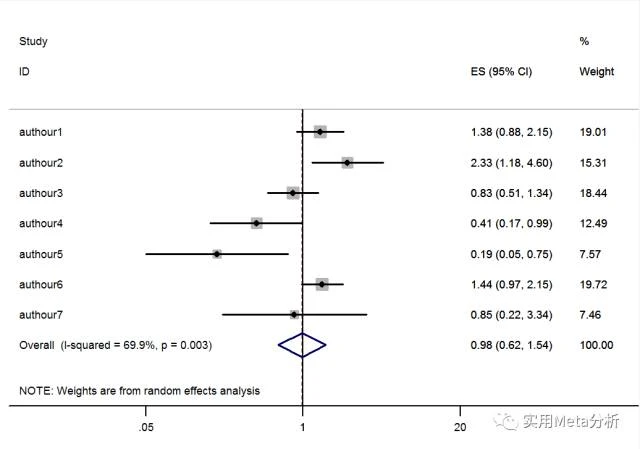
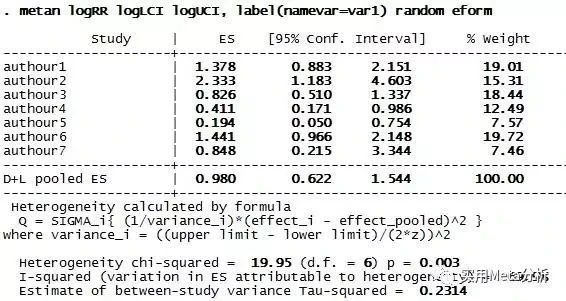
先取对数,后进行meta分析,结果如下:RR(95%CI)=0.98 (0.62, 1.54), P=0.2314>0.05,无疑更为合理。
今天的分享就到这里了~遇到任何问题欢迎后台私信哦~
