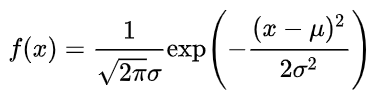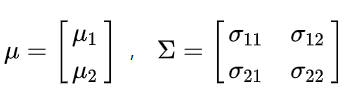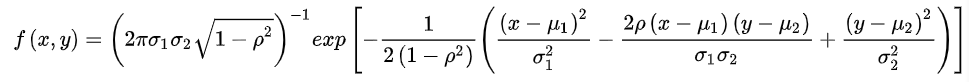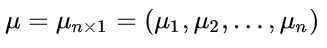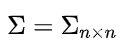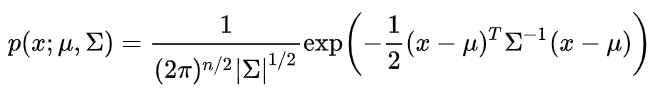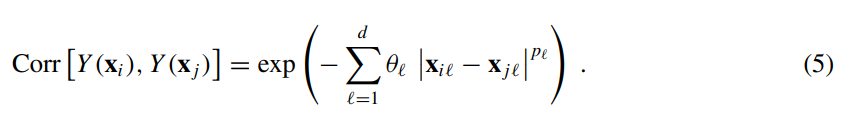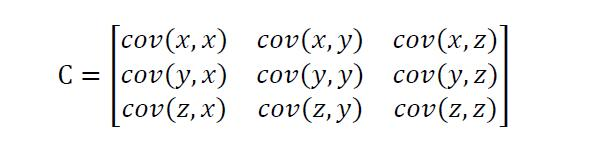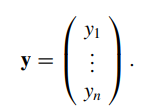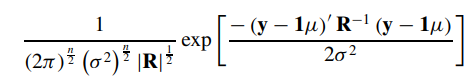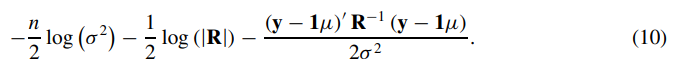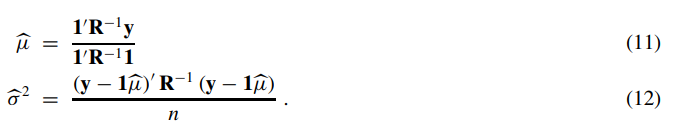简介:Kriging模型是一种通过已知试验点信息来预测未知试验点上响应的无偏估计模型,其最早是由南非矿业工程师D.G.Krige于1951年提出。20世纪70年代,法国的数学家G.Matheron对D.G.Krige的研宄成果进行了进一步的系统化、理论化,并将其命名为Kriging模型。1989年Sacks等将Kriging模型推广至试验设计领域,形成了基于计算机仿真和Kriging模型的计算机试验设计与分析方法。
本文将从原理部分,解析Kriging模型的推导过程。本次克里金模型的推导的参考文献为:
A Taxonomy of Global Optimization Methods Based on Response Surfaces
。
已知给定了一些标记过的数据集
X = { x
1
,x
2
,…,x
n
}
,其对应的目标函数值为
y = { y
1
,y
2
,…,y
n
}
,注意,其中的
x
1
是一个长度为 n 的向量,
y
1
= Y(x
1
)
。我们的目标就是想通过这些已知的点,来实现对未知点的预测。
首先
,克里金模型假设所有数据服从均值为μ方差为σ
2
的n元的正态分布,也就是说这个n元正态分布函数的均值可以认为是在[ μ-3σ, μ+3σ ]的范围内变化(论文原话,实际上刻画的是不确定性)。现在我们考虑两个点 x
i
和 x
j
,在我们采样之前,是不确定这两个点的目标函数值的,然而,我们假设建模所用的函数是连续的,当距离 || xi-xj || 比较小时,y(xi)和y(xj)也倾向于高度相关。我们可以通过下面的式子来衡量相关性:
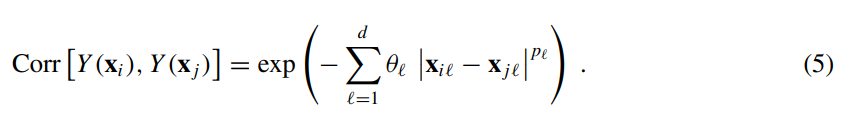
上面是论文中的描述,初学者可能会比较蒙,下面我简单解释一下:
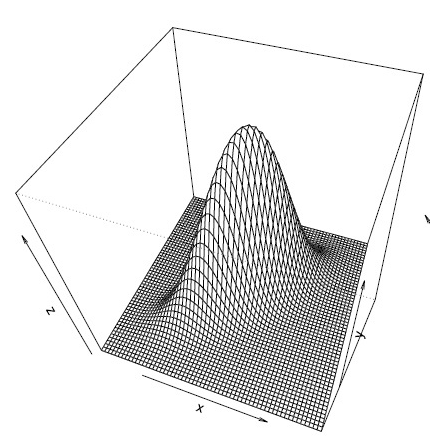
既然克里金模型假设了所有数据服从n维正态分布,那么对于n维的正态分布,如果想要刻画其pdf,最重要的就是均值和协方差了了,由于是n维,均值为各个维度的均值的组合,为nx1的矩阵,而协方差矩阵里面,非对角线上的元素就是两两随机变量之间的协方差,对角线上的元素就是各个随机变量的方差,(如下图示例,cov(z,x)刻画的是变量z和变量x之间的相关性)。论文中的式(5),就是一个刻画随机变量Y(xi)和变量Y(xj)之间的相关性的函数,属于协方差矩阵中的一员。我们令i=j,那么corr[Y(xi),Y(xj)]就为1.
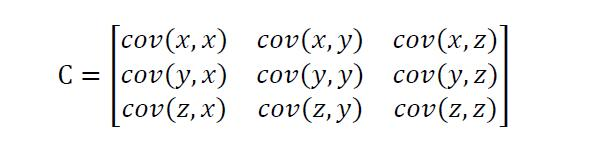
紧接着
,由于Y是服从n元正态分布,我们将n个已知点放到一起,就变成了:

Y的均值为
l
μ,其中
l
是nx1的矩阵。其协方差如下:

注意:文献中得
R
乘以了方差,文献作者应该是想表示协方差矩阵对角线上的值,不过不妨碍我们理解,这里我补充出Cov(Y)的表达式,见下图:
\begin{pmatrix} Corr[Y(X1,X1)]&...&Corr[Y(X1,Xn)]\\ ...&...&...\\ Corr[Y(Xn,X1)]&...&Corr[Y(Xn,Xn)]\\ \end{pmatrix}
⎝
⎛
C
o
r
r
[
Y
(
X
1
,
X
1
)
]
.
.
.
C
o
r
r
[
Y
(
X
n
,
X
1
)
]
.
.
.
.
.
.
.
.
.
C
o
r
r
[
Y
(
X
1
,
X
n
)
]
.
.
.
C
o
r
r
[
Y
(
X
n
,
X
n
)
]
⎠
⎞
上式中的对角线上的值就是向量各自的方差。
这里的
R
的大小为n x n的矩阵,该矩阵中的每个值都是由公式(5)得到的,i和j都是从1取到n。对角线上i=j,所以
R
为1,那么协方差
Cov(Y)
的对角线就是方差。
由上公式可知超参数有μ、σ
2
,θ
l
和p
l
(l=1,2,3…d),我们用观测数据
y
进行最大化似然来估计这些超参数,观测数据
y
如下所示:
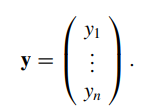
由于服从多维正态分布,最大似然的式子可以写为:
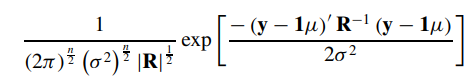
为了方便运算,取对数:
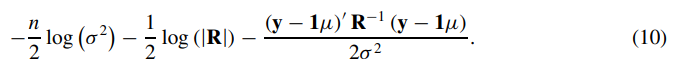
下面分别对均值μ、和方差σ
2
求偏导,即可得到使似然函数最大的均值和方差了,得到结果如下:
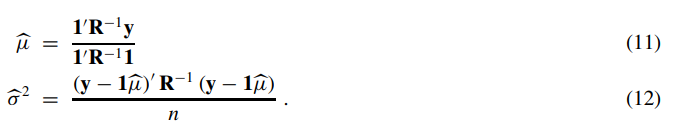
最后,将公式(11)和(12)带入到式(10)中得到log最大似然为:

由式13可知,log最大似然仅和R有关,而R中有参数θ,因此超参数的调节就是选取合适的θ使得log似然最大,可以用遗传算法或多初始点算法求得。
在4.1中,我们对已知得数据点进行了最大似然估计,得到一些先验超参数,预测就是利用4.1得到得超参数来对未知数据点进行预测。这里考虑一个点
Kriging模型理论推导1、前言2、条件3、基础知识3.1、方差的理解3.2、概率密度函数3.3、多元正态分布4、理论推导4.1 模型建立1、前言简介:Kriging模型是一种通过已知试验点信息来预测未知试验点上响应的无偏估计模型,其最早是由南非矿业工程师D.G.Krige于1951年提出。20世纪70年代,法国的数学家G.Matheron对D.G.Krige的研宄成果进行了进一步的系统化、理论化,并将其命名为Kriging模型。1989年Sacks等将Kriging模型推广至试验设计领域,形成了基于
%%% 案例:Y = G(X,t) = -30 + x1^2*x2 - 5*x1*t + ( x2 + 1)*e^(t^2)
%%% x1~N(3.5,0.3^2), x2~N(3.5, 0.3^2), t:[0,0.5]
%%% 本程序可以无偿使用,但不对实际结果做保证。
%%% 2020.08
确定变量空间
在进行实验设计前需要确定变量空间,如果变量是正太分布,那么理论上变量空间是[-∞\infty∞,+∞\infty∞],很明显不能做到,因此研究人员提出了很多确定方法,例如根据预估失效概率的大小1、使用MCS法。
一般情况...
Dace工具箱内dacefit函数自带theta 优化,只需在初始设置 theta0、lob 和upb即可。
猜测初始值theta0的选取,不影响最终结果。但是影响计算效率和加点数。
Dace工具箱手册内给的算例为:
theta=[10 10]; lob=[1e-1 1e-1]; upb=[20 20];
[dmodel,...
MATLAB是一个功能强大的数学软件,可以用于许多科学和工程应用,其中包括地理空间插值技术中的
克里金
模型
。
要使用MATLAB编写
克里金
模型
,您需要使用
kri
gin
g函数。该函数需要输入一组数据点和一组采样点,并使用
克里金
插值来计算采样点的值。
具体的步骤可以参考下面的代码示例:
1. 导入数据:
data = load('data.mat');
2. 定义采样点:
[x,y] = meshgrid(0:0.1:10,0:0.1:10);
sample_points = [x(:) y(:)];
3. 定义
克里金
模型
:
model = fitc
kri
gin
g(data(:,1:2),data(:,3),'
Kri
gin
gMethod','linear','Trend','constant');
4. 计算采样点的值:
[~,~,sample_values] = predict(model,sample_points);
5. 可视化结果:
surf(x,y,reshape(sample_values,size(x)));
这是一个简单的示例,您可以根据实际情况进行调整。希望这可以帮助到您。