参考
Tikhonov正则化选取的方法 - 云+社区 - 腾讯云
最小二乘矩阵求解与正则化，最小二乘是最常用的线性参数估计方法，早在高斯的年代，就用开对平面上的点拟合线，对高维空间的点拟合超平面。
作为最小二乘代价函数的改进
式中 ℷ >0 则称为正则化参数 (regularization parameters)
代价函数关于变元 x 的共轭梯度
使得
替代协方差矩阵的直接求逆
的方法常称为Tikhonov 正则化
在信号处理和图像处理中有时也称为松弛法(relaxation method)
Tikhonov 正则化的本质是通过对非满秩的矩阵A的协方差矩阵
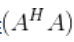的每一个对角元素加入一个很小的扰动
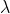
使得奇异的协方差矩阵
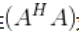求逆变为非奇异矩阵
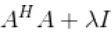的求逆，从而大大改善求解非满秩矩阵
的数值稳定性 也就是降低cond条件数的大小。
增加的项对其施加一个惩罚，其得到的解比仅优化
更切合实际
如果矩阵A是满秩矩阵，但存在误差或者噪声是，需要采用与上面相反的做法，就是对上面的协方差矩阵
加上以恶搞很小的扰动矩阵
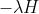去干扰，类似于上面的公式
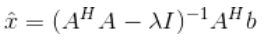
使分离噪声。
其实这两个公式可以合并，
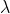本身就带有符号属性，当取得正值的时候是对矩阵的约束，迫使原来的对角协方差元素减少，
取得负值的时候就是分离残差.取0的时候就是普通最小二乘。
参数
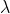是使得原始目标函数值尽可能小的同时保证
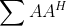不能太大，在二者取得一个很好的平衡。
最小二乘矩阵求解与正则化，最小二乘是最常用的线性参数估计方法，早在高斯的年代，就用开对平面上的点拟合线，对高维空间的点拟合超平面。作为最小二乘代价函数的改进式中 ℷ >0 则称为正则化参数 (regularization parameters)代价函数关于变元 x 的共轭梯度令得到使得替代协方差矩阵的直接求逆的方法常称为Tikhonov 正则化在信...
Tikhonov
正则化
首先我们先给出
Tikhonov
正则化
方法
我们在学习研究反问题和正则化的文章时，往往会直接给出如上定理，但
Tikhonov
泛函和解的给出并没有作过多解释，因此，接下来的内容主要是推导和理解以上内容。
我们在解决如Ax=y的线性算子方程时，通常采用经典的最小二乘法估计，但是这种
方法
会导致过拟合或者产生方程的欠定解。解决过拟合的一种
方法
就是正则化
方法
。
最小二乘法 ：最小二
最近看了看吉洪诺夫正则化
方法
，对其基本内容作了一个简单的了解。现在总结如下。
1、正则化
定义：正则化(regularization)，是指在线性代数理论中，不适定问题通常是由一组线性代数方程定义的，而且这组方程组通常来源于有着很大的条件数的不适定反问题。大条件数意味着舍入误差或其它误差会严重地影响问题的结果。
另外给出一个解释性定义：对于线性方程Ax=b，当解x不存在或者解不唯一时，就是所谓
1 、引言
在监督学习算法中，尽管过程不同，但它们都有一个共同点:
通过样本训练一个网络，对于给定的输入模式给出输出模式，等价于构造一个超平面（即多维映射），用输入模式定义输出模式。
从样本中学习是一个可逆的问题，因为其公式是建立在由相关直接问题的实例中获得的知识之上，后一类问题包含潜在的未知物理定律，但是，在现实情况下我们通常发现训练样本会受到极大的局限：
训练样本包含的信息内容通常不能够充分地...
解连续依赖于初始边界条件（the solution’s behavior changes continuously with the initial conditions）
称适定问题。只要其中一个条件不满足，则称为不适定问题[1]
在数学、统计和计算机科学尤其是在机器学习和反演问题中，正则化通过引入额外的信息去解决不适定...
### 回答1：
Tikhonov
正则化是一种在线性回归中使用的正则化
方法
，它可以减少过拟合的问题，提高模型的泛化能力。在MATLAB中，我们可以使用"
Tikhonov
正则化"函数实现该正则化
方法
。
该函数的基本语法如下：
x =
tikhonov
(A,b,lambda)
其中，A为设计矩阵，b为响应向量，lambda为正则化参数。它返回一个列向量x，表示正则化后的解。
该函数在实现
Tikhonov
正则化时采用的是奇异值分解（SVD）
方法
。它将设计矩阵分解为三个矩阵的乘积，通过求解这三个矩阵的逆来获得正则化解。
在使用该函数时，需要手动指定正则化参数lambda的值。通常来说，这个值可以通过交叉验证的
方法
来确定。如果lambda取值过小，正则化作用将较弱，容易出现过拟合；如果lambda取值过大，正则化作用将较强，容易出现欠拟合。
总的来说，
Tikhonov
正则化是一种非常实用的线性回归正则化
方法
。使用MATLAB中的相关函数可以方便地实现该
方法
。但是需要注意的是，正则化参数的
选取
并不是唯一的，需要根据实际情况进行调整。
### 回答2：
Tikhonov
正则化是一种正则化
方法
，用于解决线性最小二乘问题的不稳定性。它是通过在原始的最小二乘问题中添加一个正则化项来实现的，以惩罚过大的参数值。
Matlab中可以使用lsqnonneg函数来进行
Tikhonov
正则化。该函数的使用
方法
如下：
[x,resnorm]=lsqnonneg(A,b,lambda);
其中，A是一个m×n的矩阵，b是一个m维向量，lambda是正则化参数。函数返回一个n维向量x，表示最小化系统(Ax-b)的平方和的解，同时返回平方和的值resnorm。
需要注意的是，正则化参数lambda的选择是很重要的。如果选择的lambda太小，那么可能无法有效地惩罚参数值过大的情况，解可能会过拟合；而如果lambda太大，那么可能会抑制有用的信息，导致欠拟合的结果。
因此，通常需要进行交叉验证来选择最佳的lambda值。交叉验证的基本思想是将数据分为训练集和测试集，然后使用训练集来训练模型，使用测试集来评估模型的性能。可以尝试不同的lambda值，并选择性能最好的lambda值作为最终参数。
在使用
Tikhonov
正则化的过程中，需要注意一些问题。由于正则化项是基于参数值的平方和，因此对于一个精确解来说，它应该等于零。如果正则化项的值不为零，那么可能是由于矩阵A的列之间存在线性相关性，需要考虑去除冗余的列。
此外，
Tikhonov
正则化可以应用于非线性最小二乘问题，只需要将非线性问题转化为线性问题，然后使用
Tikhonov
正则化来解决即可。通常可以使用牛顿-拉夫逊
方法
或高斯-牛顿
方法
来实现这种转换。
总之，
Tikhonov
正则化是一种非常有用的正则化
方法
，可以用于解决最小二乘问题的不稳定性。在使用时需要注意正则化参数的选择和数据的预处理，以获得最佳的效果。
### 回答3：
Tikhonov
正则化是一种经验风险最小化
方法
，通过在目标函数中加入正则化项，可以有效避免过拟合的问题。
Tikhonov
正则化一般用在线性回归问题中，即为常见的岭回归。
在Matlab中，使用
Tikhonov
正则化可以通过调用“ridge”函数来实现。该函数的输入参数包括训练数据及其标签、正则化系数和截距项。其中，正则化系数越大，模型复杂度越低，越容易避免过拟合。
下面是一个简单的
Tikhonov
正则化Matlab程序示例：
``` matlab
% 读取训练数据
load('traindata.mat');
% 设定正则化系数lambda
lambda = 0.1;
% 执行
Tikhonov
正则化
[B, FitInfo] = ridge(traindata(:,2:end), traindata(:,1), lambda, 'intercept',true);
% 输出模型参数
disp('模型参数:');
disp(B);
% 输出R方值
disp('R方值:');
disp(FitInfo.rsquare);
以上程序的作用是读取训练数据，设定正则化系数lambda，然后执行
Tikhonov
正则化，最后输出模型参数和R方值。其中，“traindata”为一个M*N+1的矩阵，其中第一列是训练数据的标签，后面N列是特征值。在执行
Tikhonov
正则化时，使用了Matlab内置的“ridge”函数，其返回值包括模型参数“B”和FitInfo结构体。在输出模型参数和R方值时，使用了Matlab内置的“disp”函数。
