先看下百度百科的介绍:最小二乘法(又称最小平方法)是一种
数学
优化技术。它通过最小化
误差
的平方和寻找数据的最佳
函数
匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间
误差
的平方和为最小。最小二乘法还可用于
曲线拟合
。其他一些优化问题也可通过最小化
能量
或最大化熵用最小二乘法来表达。
通过这段描述可以看出来,最小二乘法也是一种优化方法,求得目标函数的最优值。并且也可以用于曲线拟合,来解决回归问题。难怪《统计学习方法》中提到,回归学习最常用的损失函数是平方损失函数,在此情况下,回归问题可以著名的最小二乘法来解决。看来最小二乘法果然是机器学习领域做有名和有效的算法之一。
最小二乘法
我们以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢? 监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。回归分析中,如果只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。对于二维空间线性是一条直线;对于三维空间线性是一个平面,对于多维空间线性是一个超平面...
对于一元线性回归模型, 假设从总体中获取了n组观察值(X1,Y1),(X2,Y2), …,(Xn,Yn)。对于平面中的这n个点,可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看,这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小。有以下三个标准可以选择:
(1)用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
(2)用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
(3)最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外,得到的估计量还具有优良特性。这种方法对异常值非常敏感。
最常用的是普通最小二乘法( Ordinary Least Square,OLS):所选择的回归模型应该使所有观察值的残差平方和达到最小。(Q为残差平方和)- 即采用平方损失函数。
样本回归模型:
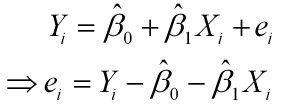 其中e
i
为样本(X
i,
Y
i
)的误差
其中e
i
为样本(X
i,
Y
i
)的误差
平方损失函数:
则通过Q最小确定这条直线,即确定
 ,以
,以
 为变量,把它们看作是Q的函数,就变成了一个求极值的问题,可以通过求导数得到。求Q对两个待估参数的偏导数:
为变量,把它们看作是Q的函数,就变成了一个求极值的问题,可以通过求导数得到。求Q对两个待估参数的偏导数:
根据数学知识我们知道,函数的极值点为偏导为0的点。
这就是最小二乘法的解法,就是求得平方损失函数的极值点。
下面通过一个例子来说明最小二乘法:
最小二乘法
概述
最小二乘法
(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用
最小二乘法
可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法
还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用
最小二乘法
来表达。
简而言之,
最小二乘法
同梯度下降类似,都是一种求解无约束最优化问题的常用方法,并且也可以用于曲线拟合,来解决回归问题。
一元线性模型
如果以最简单的一元线性模型来解释
最小二乘法
。回归分析中,如果只包括一个自变量和
最小二乘法
可以在给定一组数据集和一个模型的情况下,通过求解残差(即预测值和实际值之间的差)平方和的最小值,找到回归系数的最优解。总的来说,
最小二乘法
是一种简单有效的线性回归方法,它可以帮助我们在给定数据集和模型的情况下,求解模型中的参数并找到最优解。
最小二乘法
的思路非常简单,即针对给定的数据集,构建一个线性模型,然后通过最小化残差平方和来求解模型的参数。其中,y表示预测值,x1~xn表示模型的输入特征,w1~wn表示各个特征对应的权重,b表示截距。其中,x1_i~xn_i是样本data_i的各个特征值。
一、
最小二乘法
理解:
先从最小二乘的名字来看,所谓最小二乘,其实也可以叫做最小平方和。那么,是什么的平方和最小呢?那肯定是误差最小,那是什么的误差呢?就是目标对象和拟合对象的误差。连起来看,就是通过最小化误差的平方和,使得拟合对象无限接近目标对象,这就是最小二乘的核心思想。可以看出,最小二乘解决的是一类问题,就是需要拟合现有对象的问题。这么看来,是不是也就可以理解为什么最小二乘应用如此广...
这几天在刷B站的时候,有个深度学习的博主推荐了一本
机器学习
的书——《白话
机器学习
的数学》,抱着浅看一下的态度,我花3个大洋从淘宝上找到了这本书的电子版。看了两天我直接吹爆!!!所以这个专栏,就分享一下我在
机器学习
中的学习笔记及一些感悟,也希望对你的学习有帮助哦!感兴趣的小伙伴欢迎私信或者评论区留言!
概念:
最小二乘法
是一种熟悉而优化的方法。主要是通过最小化误差的平方以及最合适数据的匹配函数。
作用:(1)利用
最小二乘法
可以得到位置数据(这些数据与实际数据之间误差平方和最小)(2)也可以用来曲线拟合
实例讲解:有一组数据(1,6),(3,5),(5,7),(6,12),要找出一条与这几个点最为匹配的直线 : y = A + Bx
有如下方程:
6 = A + B
5 = A + 3B ...
       
机器学习
金典
算法
系列旨在归纳总结常用
经典
机器学习
算法
,其中内容来自自己学习理解、博文参考等,目的在于再次深入学习这类
算法
,并加以总结,提升自我,方便文档查阅;如有不足,请
5月9号到北大去听hulu的讲座《推荐系统和计算广告在视频行业应用》,想到能见到传说中的项亮大神,特地拿了本《推荐系统实践》求签名。讲座开始,主讲人先问了下哪些同学有
机器学习
的背景,我恬不知耻的毅然举手,真是惭愧。后来主讲人在讲座中提到了
最小二乘法
,说这个是
机器学习
最基础的
算法
。神马,最基础,我咋不知道呢! 看来以后还是要对自己有清晰认识。
回来赶紧上百度,搜了下...
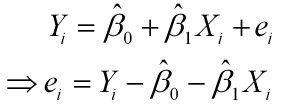 其中e
i
为样本(X
i,
Y
i
)的误差
其中e
i
为样本(X
i,
Y
i
)的误差
 ,以
,以
 为变量,把它们看作是Q的函数,就变成了一个求极值的问题,可以通过求导数得到。求Q对两个待估参数的偏导数:
为变量,把它们看作是Q的函数,就变成了一个求极值的问题,可以通过求导数得到。求Q对两个待估参数的偏导数: