FM因子分解机的原理、公式推导、Python实现和应用
因子分解机模型,即Factorization Machines Model,简称FM。
FM模型可以用于回归任务、二分类任务、排名任务,特别是在数据稀疏场景下,效果明显,广泛应用于推荐系统、广告系统等领域。
目前来看,FM模型是推荐系统、广告系统的三大基础模型之一,如果想从事推荐、广告相关的工作、研究、学习,是必须要掌握的。
本文首先回顾正定矩阵、Cholesky分解、线性回归模型,二阶多项式回归模型等因子分解机FM模型的相关基础知识,说明FM的起源及数学背景;接着,介绍FM模型的原理,详细公式推导,公式化简、损失函数、训练(学习)、特征工程等;然后,指出FM模型在二分类、抖音短视频推荐等方面的应用,并附上Python、TensorFlow 2 实现代码;最后,对FM模型进行总结,指出FM模型的价值,并与线性回归模型、逻辑回归模型进行对比,而且指出FM、FFM、DeepFM、xDeepFM的演化过程。本文目录如下:
一、FM模型基础
1、FM模型提出
2、共轭转置矩阵
3、正定矩阵
4、Cholesky 分解
5、线性回归模型
6、二阶多项式回归模型
二、FM模型原理
1、FM模型原理
2、FM模型化简
3、FM模型损失函数
4、FM模型训练
5、FM模型特征工程
三、FM模型应用
1、libFM实战
2、FM二分类(Python实现)
3、FM的TensorFlow实现
4、FM抖音短视频推荐实践
四、FM模型总结
1、FM模型优点
2、线性回归 VS FM
3、LR VS FM
4、FM模型演化
直接上PPT

一、FM模型基础
注意:第一部分是为了说明FM的起源及数学背景,跳过第一部分不影响第二部分的阅读。
1、FM模型提出
2010年,FM模型由 Steffen Rendle在论文《Factorization Machines》提出:
强烈推荐原始论文,写的详细明白,非常棒,非常棒,非常棒。

2、 共轭转置矩阵
什么是转置矩阵(Transpose)、共轭转置矩阵(Conjugate Transpose)?

3、正定矩阵
正定矩阵(Positive Definite Matrix)是一种实对称矩阵。

4、Cholesky 分解
Cholesky 分解,即楚列斯基分解(Cholesky Decomposition),也称乔里斯基分解。

5、线性回归模型
什么是线性回归模型?详情可参考:

线性回归模型假设特征之间是相互独立的、不相关的。但在现实的某些场景中,特征之间往往是相关的,而不是相互独立的。比如<女性>和<化妆品>,<程序员>与<计算机类书籍>。
所以有些场景需要特征组合。
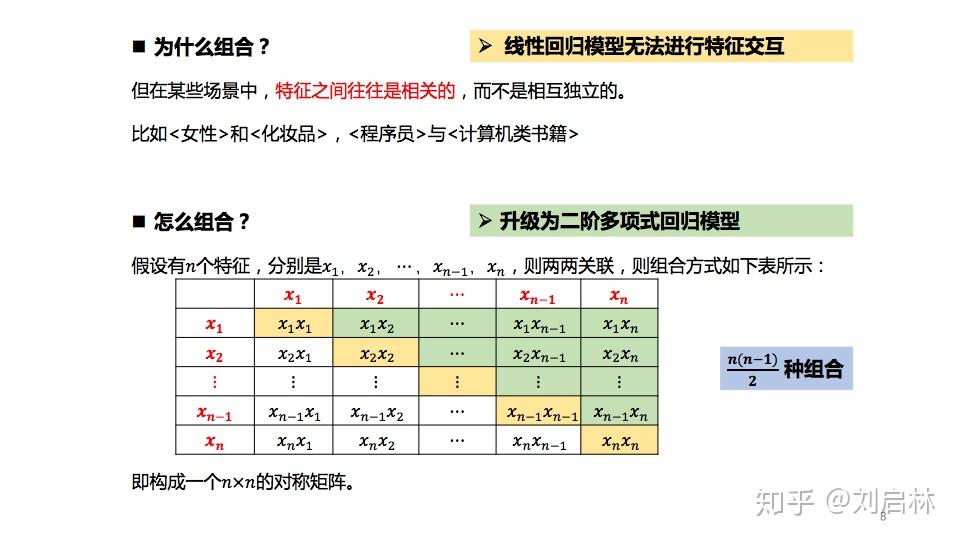
6. 二阶多项式回归模型
特征两两组合,得到二阶多项式回归模型。

特征关系的向量化,则得FM模型。

二、 FM模型原理
1、FM模型原理
FM模型假设特征两两相关。
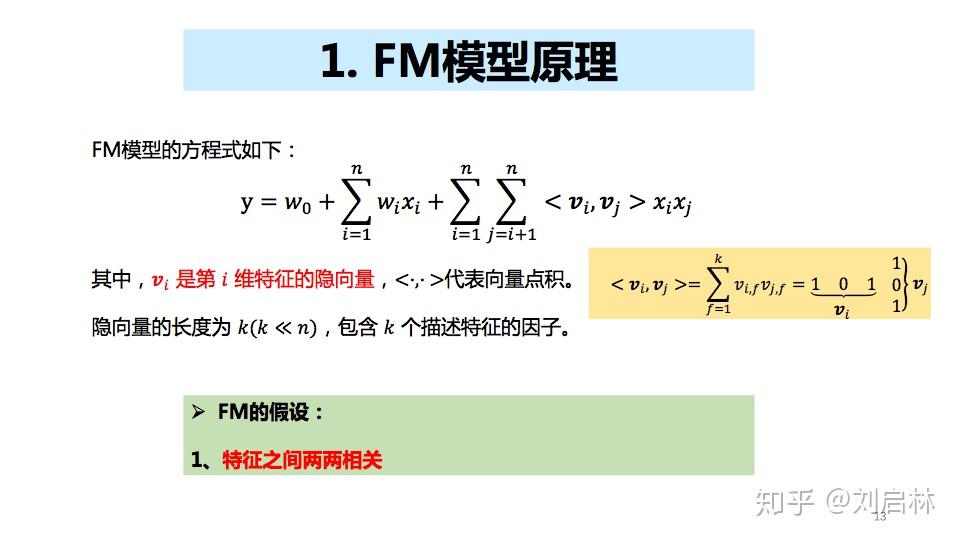
FM模型关键是:特征两两相关。

2、FM模型化简
代数推导FM组合关系如下:
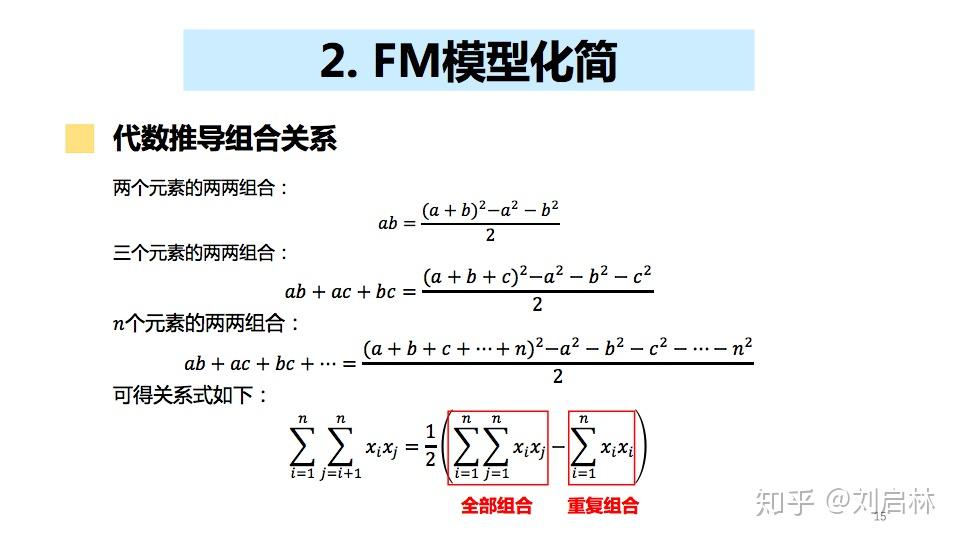
利用矩阵直观化推导FM模型的计算,具体推导如下:
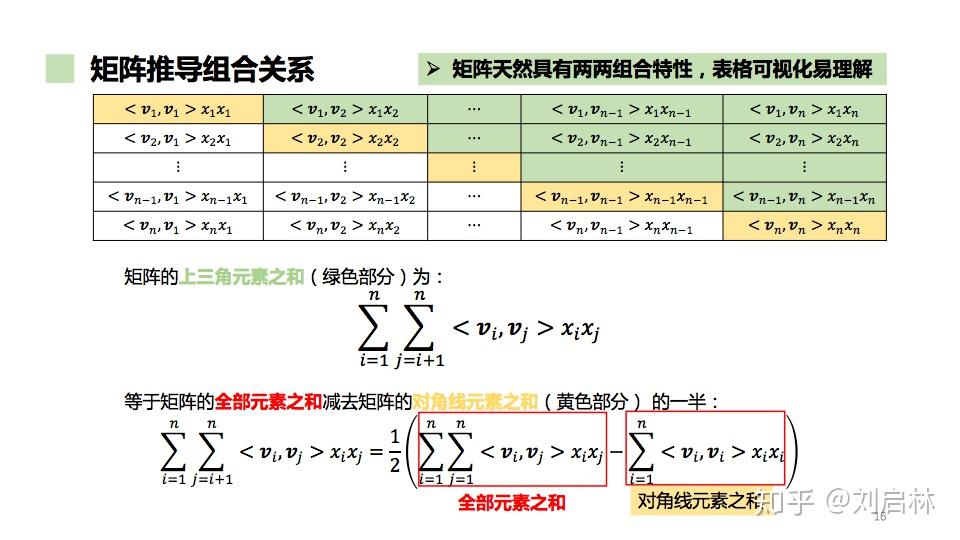
FM模型的二次项 等价化简 过程如下:

FM模型最后化简如下图所示:

FM模型的时间复杂度降级到线性。
3、FM模型损失函数
FM模型可用于回归(Regression)、二分类(Binary classification)、排名(Ranking)任务,其对应的损失函数如下:

FM的二分类问题,需要借助 LR 模型转化成二分类问题。
按 y 取值(标注),分为 y∈{0, 1} 和 y∈{-1, 1}。
假设,聚焦 FM 的二分类交叉熵损失函数,其公式表达如下:

FM 的二分类交叉熵损失函数的公式推导,可参考《LR逻辑回归模型的原理、公式推导、Python实现和应用》的第二部分的LR损失函数。
4、FM模型训练
FM的训练(学习)算法主要有三种:
- 随机梯度下降法(Stochastic Gradient Descent,SGD)
- 交替最小二乘法(Alternating Least-Squares,ALS)
- 马尔科夫链蒙特卡洛法(Markov Chain Monte Carlo,MCMC)
详细的FM模型训练,可以参考Steffen Rendle的论文《Factorization Machines with libFM》,写的很全面。
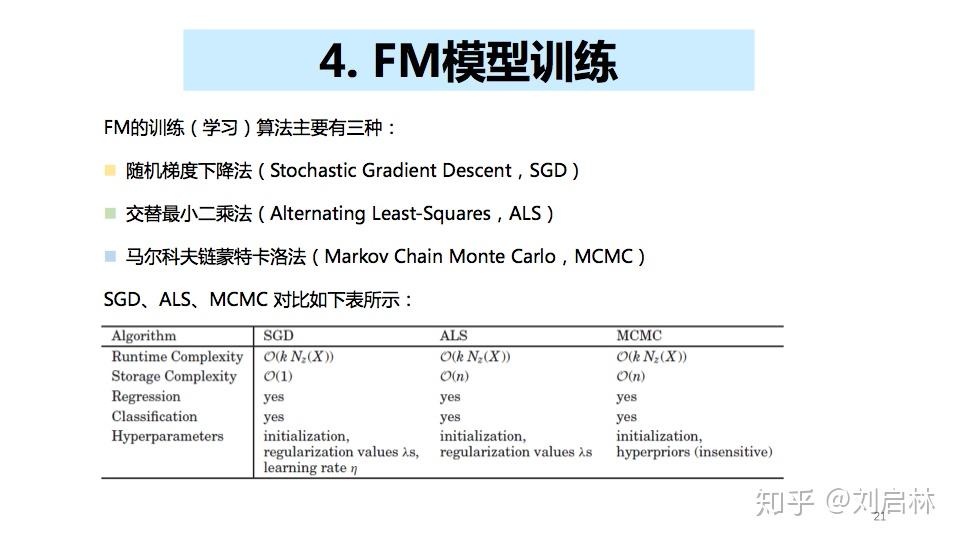
采用随机梯度下降法(SGD)对FM进行训练。

假设数据集的标记y∈{-1,1},则用梯度下降法对FM训练(学习)公式推导如下:

备注:FM实现随机梯度下降训练的代码见第三部分“FM模型应用”。
5. FM模型特征工程
FM模型对特征两两自动组合,不需要人工参与,类别特征One-Hot化。

举个FM特征工程的例子。已知一个电影数据集如下:
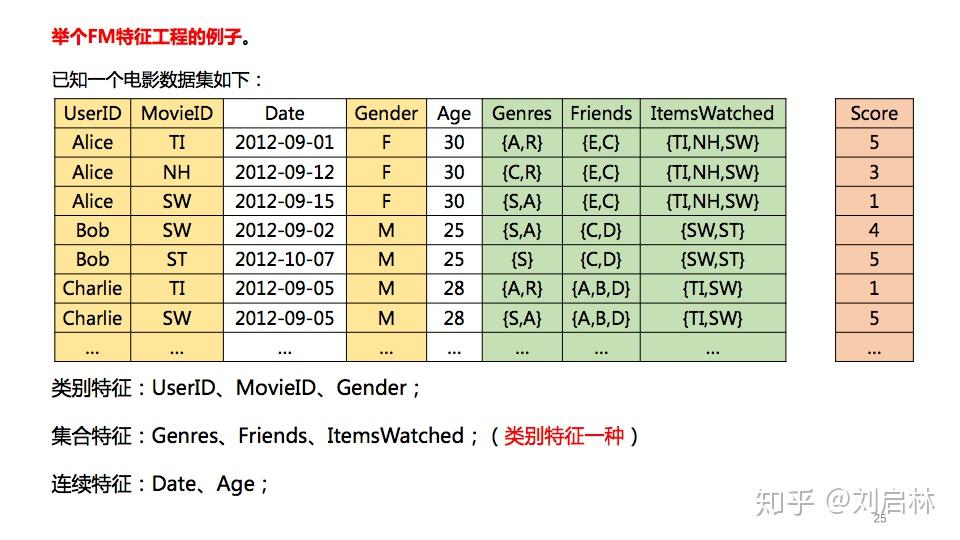
其中,黄色部分是类别特征;绿色部分是集合特征;白色部分是连续特征。
电影数据集,FM特征化之后得:
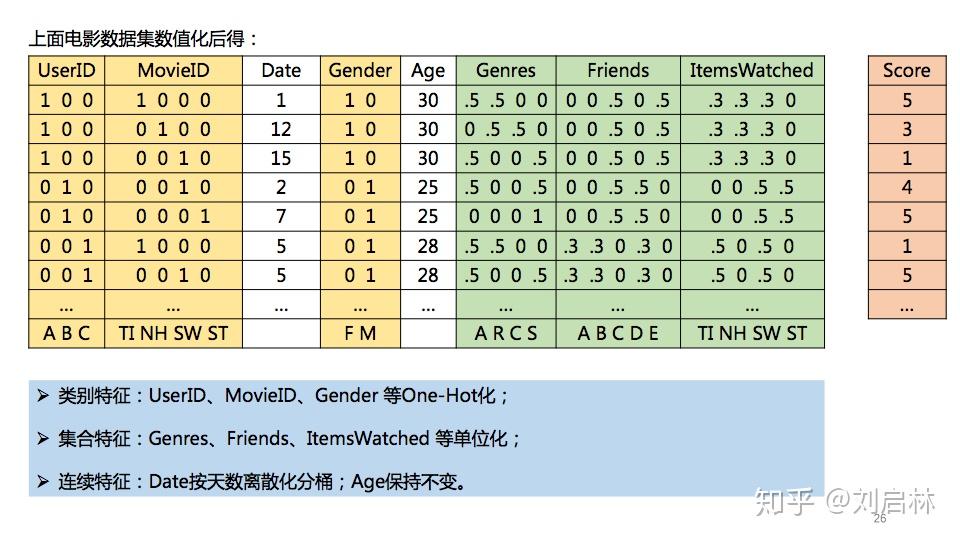
注意:.5 = 0.5,一种简化表示。
FM特征的二次项交互如下图所示:
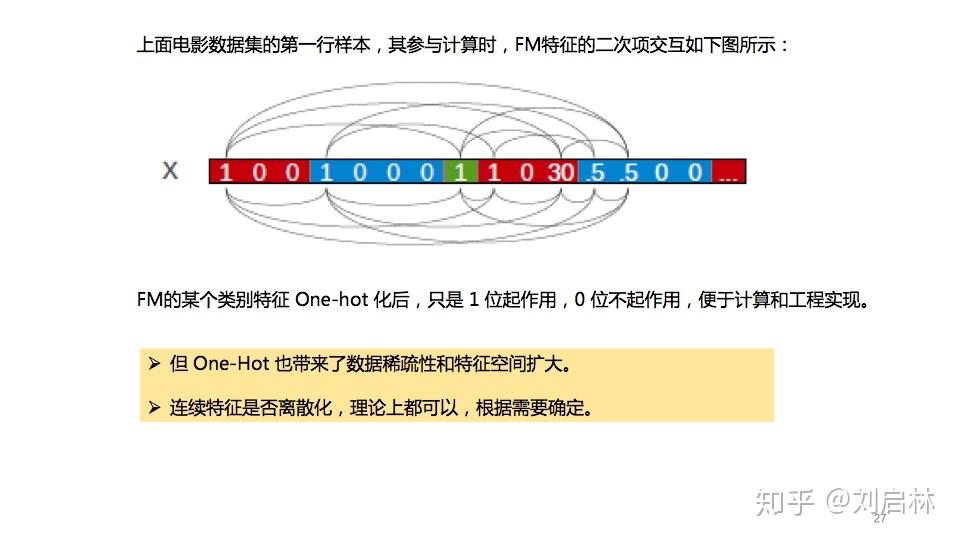
FM的某个类别特征 One-Hot 化后,只是1位起作用,0位不起作用,便于计算和工程实现。
注意,FM的连续特征是否离散化,理论上都可以,根据需要确定。
三、FM模型应用
为了全面、完整的说明FM模型在二分类上的应用,特举4个例子(或者说是4个视角)如下:
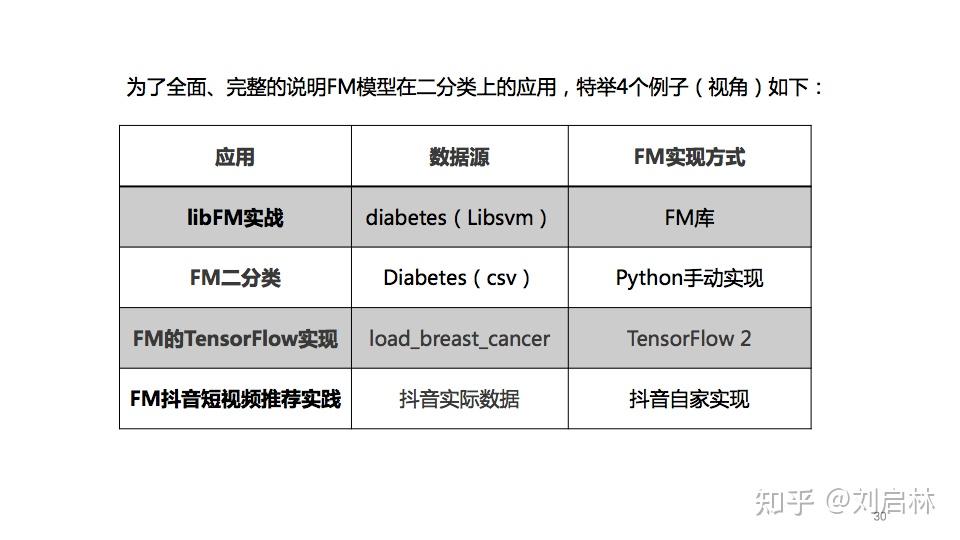
1、libFM实战
libFM是Steffen Rendle开发的FM模型库。更详细信息可以在官网获得。

举个基于libFM的例子。
数据集:diabetes
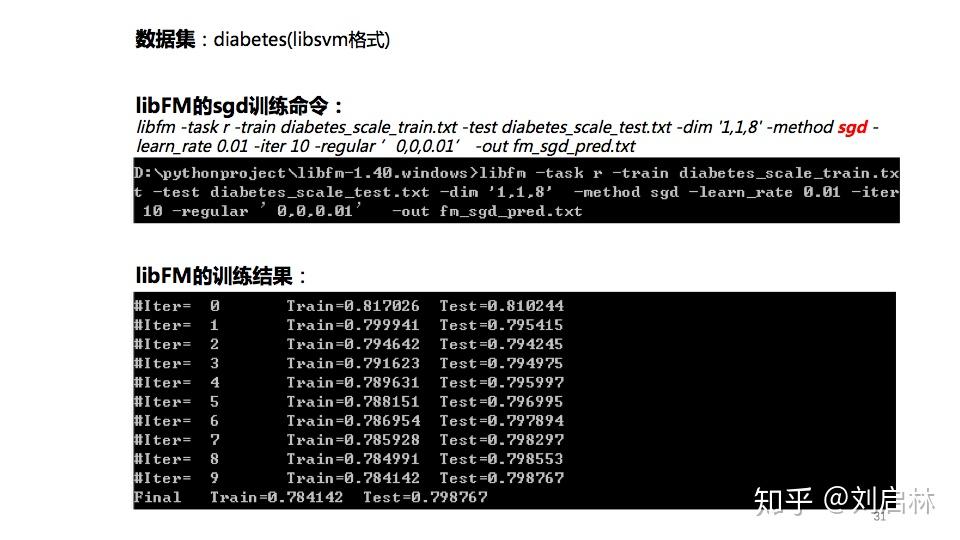
windows命令如下:
libfm -task r -train diabetes_scale_train.txt -test diabetes_scale_test.txt -dim '1,1,8' -method sgd -learn_rate 0.01 -iter 10 -regular ’0,0,0.01’ -out fm_sgd_pred.txt
参数说明见《libFM 1.4.2 - Manual》
2、FM二分类
基于Python手动实现FM算法,并进行二分类预估。

数据集:diabetes.csv
可以从Github上下载:diabetes.csv
数据集切分代码如下:
import numpy as np
import random
# 数据集切分
def loadData(fileName,ratio): # ratio,训练集与测试集比列
trainingData = []
testData = []
with open(fileName) as txtData:
lines = txtData.readlines()
for line in lines:
lineData = line.strip().split(',')
if random.random() < ratio: #数据集分割比例
trainingData.append(lineData) #训练数据集列表
else:
testData.append(lineData) #测试数据集列表
np.savetxt('../data/diabetes_train.txt', trainingData, delimiter=',',fmt='%s')
np.savetxt('../data/diabetes_test.txt', testData, delimiter=',',fmt='%s')
return trainingData,testData
diabetes_file = '../data/diabetes.csv'
trainingData, testData = loadData(diabetes_file,0.8)FM二分类的随机梯度下降训练代码如下:
# FM二分类
# diabetes皮马人糖尿病数据集
# coding:UTF-8
from numpy import *
from random import normalvariate # 正态分布
from datetime import datetime
import pandas as pd
import numpy as np
# 处理数据
def preprocessData(data):
feature = np.array(data.iloc[:, :-1]) # 取特征(8个特征)
label = data.iloc[:, -1].map(lambda x: 1 if x == 1 else -1) # 取标签并转化为 +1,-1
# 将数组按行进行归一化
zmax, zmin = feature.max(axis=0), feature.min(axis=0) # 特征的最大值,特征的最小值
feature = (feature - zmin) / (zmax - zmin)
label = np.array(label)
return feature, label
def sigmoid(inx):
return 1.0 / (1 + np.exp(-inx))
# 训练FM模型
def FM(dataMatrix, classLabels, k, iter, alpha):
:param dataMatrix: 特征矩阵
:param classLabels: 标签矩阵
:param k: v的维数
:param iter: 迭代次数
:return: 常数项w_0, 一阶特征系数w, 二阶交叉特征系数v
# dataMatrix用的是matrix, classLabels是列表
m, n = shape(dataMatrix) # 矩阵的行列数,即样本数m和特征数n
# 初始化参数
w = zeros((n, 1)) # 一阶特征的系数
w_0 = 0 # 常数项
v = normalvariate(0, 0.2) * ones((n, k)) # 即生成辅助向量(n*k),用来训练二阶交叉特征的系数
for it in range(iter):
for x in range(m): # 随机优化,每次只使用一个样本
# 二阶项的计算
inter_1 = dataMatrix[x] * v # 每个样本(1*n)x(n*k),得到k维向量(FM化简公式大括号内的第一项)
inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v) # 二阶交叉项计算,得到k维向量(FM化简公式大括号内的第二项)
interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2. # 二阶交叉项计算完成(FM化简公式的大括号外累加)
p = w_0 + dataMatrix[x] * w + interaction # 计算预测的输出,即FM的全部项之和
tmp = 1 - sigmoid(classLabels[x] * p[0, 0]) # tmp迭代公式的中间变量,便于计算
w_0 = w_0 + alpha * tmp * classLabels[x]
for i in range(n):
if dataMatrix[x, i] != 0:
w[i, 0] = w[i, 0] + alpha * tmp * classLabels[x] * dataMatrix[x, i]
for j in range(k):
v[i, j] = v[i, j] + alpha * tmp * classLabels[x] * (
dataMatrix[x, i] * inter_1[0, j] - v[i, j] * dataMatrix[x, i] * dataMatrix[x, i])
# 计算损失函数的值
if it % 10 == 0:
loss = getLoss(getPrediction(mat(dataMatrix), w_0, w, v), classLabels)
print("第{}次迭代后的损失为{}".format(it, loss))
return w_0, w, v
# 损失函数
def getLoss(predict, classLabels):
m = len(predict)
loss = 0.0
for i in range(m):
loss -= log(sigmoid(predict[i] * classLabels[i]))
return loss
def getPrediction(dataMatrix, w_0, w, v):
m = np.shape(
dataMatrix)[0]
result = []
for x in range(m):
inter_1 = dataMatrix[x] * v
inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v) # multiply对应元素相乘
# 完成交叉项
interaction = np.sum(multiply(inter_1, inter_1) - inter_2) / 2.
p = w_0 + dataMatrix[x] * w + interaction # 计算预测的输出
pre = sigmoid(p[0, 0])
result.append(pre)
return result
# 评估预测的准确性
def getAccuracy(predict, classLabels):
m = len(predict)
allItem = 0
error = 0
for i in range(m): # 计算每一个样本的误差
allItem += 1
if float(predict[i]) < 0.5 and classLabels[i] == 1.0:
error += 1
elif float(predict[i]) >= 0.5 and classLabels[i] == -1.0:
error += 1
else:
continue
return float(error) / allItem
if __name__ == '__main__':
trainData = '../data/diabetes_train.txt'
testData = '../data/diabetes_test.txt'
train = pd.read_csv(trainData)
test = pd.read_csv(testData)
dataTrain, labelTrain = preprocessData(train)
dataTest, labelTest = preprocessData(test)
date_startTrain = datetime.now()
print("开始训练")
w_0, w, v = FM(mat(dataTrain), labelTrain, 4, 100, 0.01)
print("w_0:", w_0)
print("w:", w)
print("v:", v)
predict_train_result = getPrediction(mat(dataTrain), w_0, w, v) # 得到训练的准确性
print("训练准确性为:%f" % (1 - getAccuracy(predict_train_result, labelTrain)))
date_endTrain = datetime.now()
print("训练用时为:%s" % (date_endTrain - date_startTrain))
print("开始测试")
predict_test_result = getPrediction(mat(dataTest), w_0, w, v) # 得到训练的准确性
print("测试准确性为:%f" % (1 - getAccuracy(predict_test_result, labelTest)))基于diabetes数据集,FM的训练结果如下:

代码解析1 —— FM模型化简的代码:
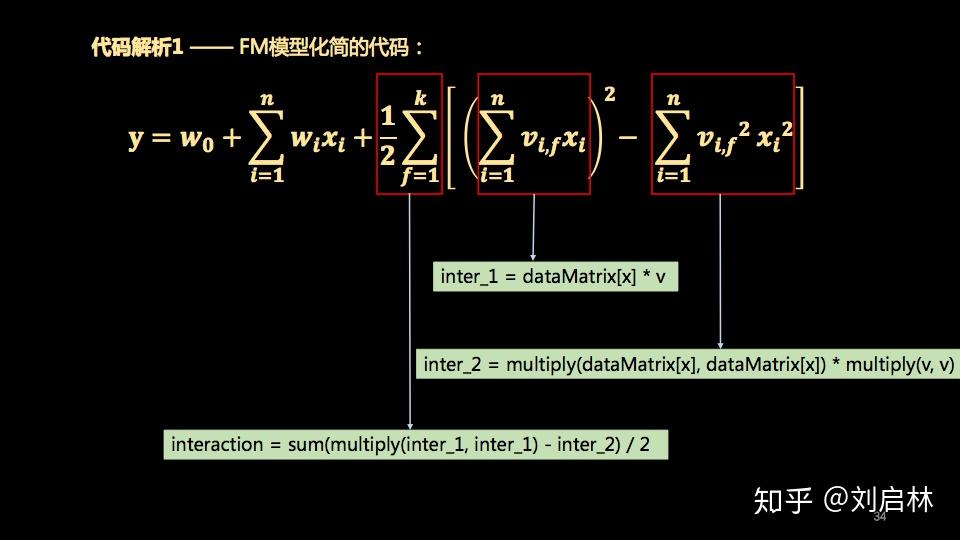
代码解析2 —— FM二分类随机梯度下降法训练 w_0 的迭代公式代码 :
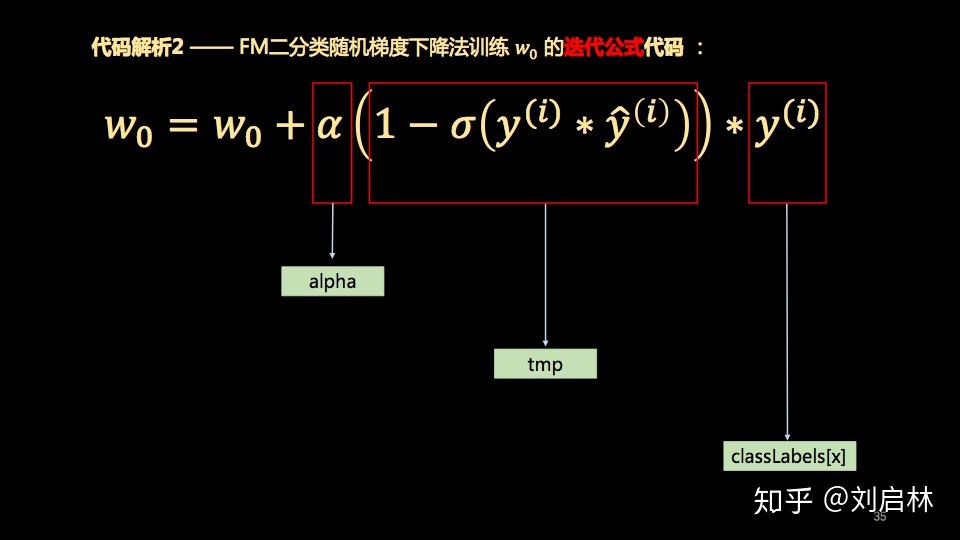
代码解析3 —— FM二分类 v(i,f) 的求导代码:

3、FM的TensorFlow实现
基于 TensorFlow 2 实现FM算法。

Python 3.7 + TensorFlow 2 + Sklearn的代码如下:
import tensorflow as tf
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
K = tf.keras.backend
# 自定义FM的二阶交叉层
class FMLayer(tf.keras.layers.Layer):
# FM的k取4(演示方便)
def __init__(self, input_dim, output_dim=4, **kwargs):
self.input_dim = input_dim
self.output_dim = output_dim
super(FMLayer, self).__init__(**kwargs)
# 初始化训练权重
def build(self, input_shape):
self.kernel = self.add_weight(name='kernel',
shape=(self.input_dim, self.output_dim),
initializer='glorot_uniform',
trainable=True)
super(FMLayer, self).build(input_shape)
# 自定义FM的二阶交叉项的计算公式
def call(self, x):
a = K.pow(K.dot(x, self.kernel), 2)
b = K.dot(K.pow(x, 2), K.pow(self.kernel, 2))
return K.sum(a-b, 1, keepdims=True)*0.5
# 输出的尺寸大小
def compute_output_shape(self, input_shape):
return input_shape[0], self.output_dim
# 实现FM算法
def FM(feature_dim):
inputs = tf.keras.Input((feature_dim,))
# 线性回归
liner = tf.keras.layers.Dense(units=1,
bias_regularizer=tf.keras.regularizers.l2(0.01),
kernel_regularizer=tf.keras.regularizers.l1(0.02),
)(inputs)
# FM的二阶交叉项
cross = FMLayer(feature_dim)(inputs)
# 获得FM模型(线性回归 + FM的二阶交叉项)
add = tf.keras.layers.Add()([liner, cross])
predictions = tf.keras.layers.Activation('sigmoid')(add)
model = tf.keras.Model(inputs=inputs, outputs=predictions)
model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
loss=tf.keras.losses.binary_crossentropy,
metrics=[tf.keras.metrics.binary_accuracy])
return model
# 训练FM模型
def train():
fm = FM(30)
data = load_breast_cancer()
# sklearn 切分数据
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2,
random_state=11, stratify=data.target)
fm.fit(X_train, y_train, epochs=5, batch_size=20, validation_data=(X_test, y_test))
return fm
if __name__ == '__main__':
fm = train()
fm.summary()训练结果如下:
基于TensorFlow训练的FM模型的结构、结果
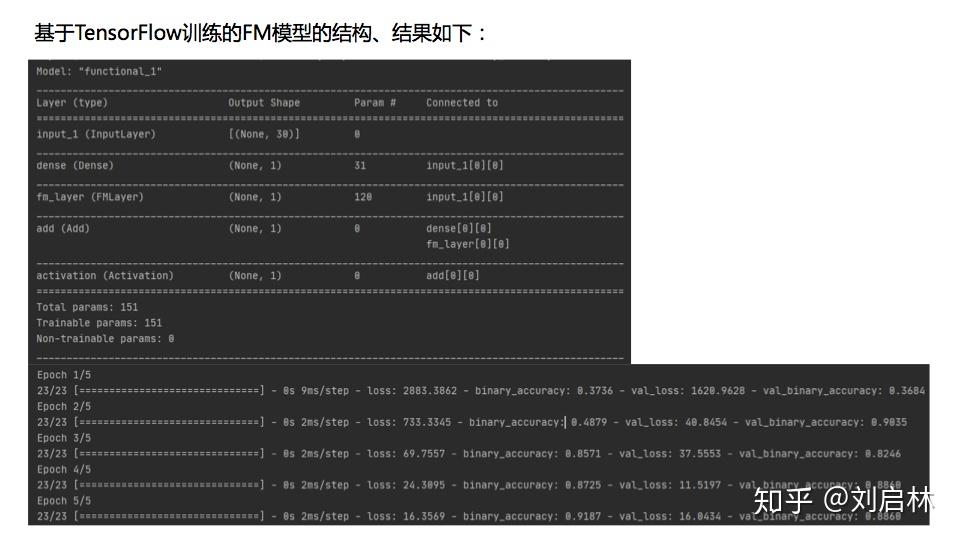
得到FM模型各参数如下:
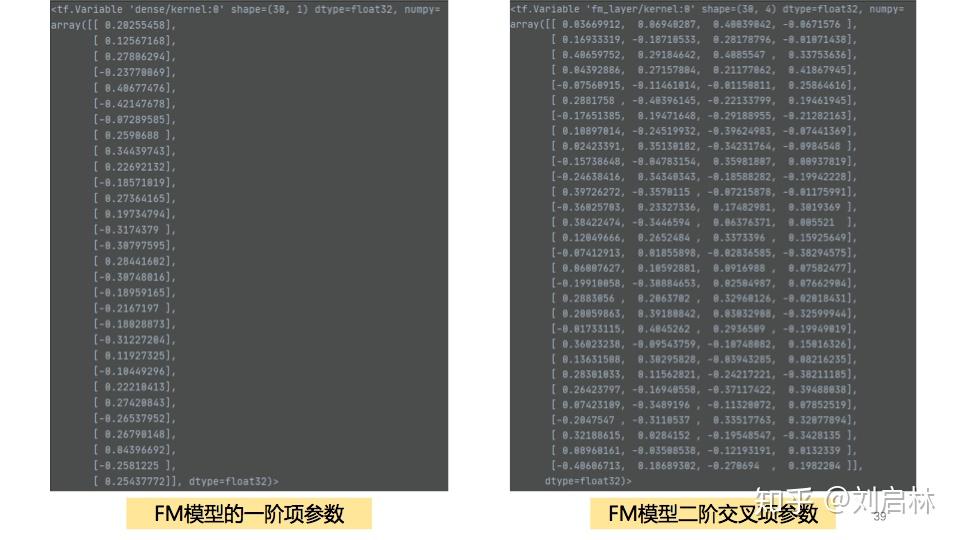
4、FM抖音短视频推荐实践
详细内容请参考: ICME2019短视频内容理解与推荐竞赛
字节跳动给了一个参考模型——FM模型(baseline)。

其中抖音实现的FM类代码如下:
import tensorflow as tf
class FMModelParams(object):
""" class for initializing weights """
def __init__(self, feature_size, embedding_size):
self._feature_size = feature_size
self._embedding_size = embedding_size
def initialize_weights(self):
""" init fm weights
Returns
weights:
feature_embeddings: vi, vj second order params
weights_first_order: wi first order params
bias: b bias
weights = dict()
weights_initializer=tf.glorot_normal_initializer()
bias_initializer=tf.constant_initializer(0.0)
weights["feature_embeddings"] = tf.get_variable(
name='weights',
dtype=tf.float32,
initializer=weights_initializer,
shape=[self._feature_size, self._embedding_size])
weights["weights_first_order"] = tf.get_variable(
name='vectors',
dtype=tf.float32,
initializer=weights_initializer,
shape=[self._feature_size, 1])
weights["fm_bias"] = tf.get_variable(
name='bias',
dtype=tf.float32,
initializer=bias_initializer,
shape=[1])
return weights
class FMModel(object):
""" FM implementation """
@staticmethod
def fm_model_fn(features, labels, mode, params):
""" build tf model"""
#parse params
embedding_size = params['embedding_size']
feature_size = params['feature_size']
batch_size = params['batch_size']
learning_rate = params['learning_rate']
field_size = params['field_size']
optimizer_used = params['optimizer']
#parse features
feature_idx = features["feature_idx"]
feature_idx = tf.reshape(feature_idx, shape=[batch_size, field_size])
labels = tf.reshape(labels, shape=[batch_size, 1])
feature_values = features["feature_values"]
feature_values = tf.reshape(feature_values, shape=[batch_size, field_size, 1])
# tf fm weights
tf_model_params = FMModelParams(feature_size, embedding_size)
weights = tf_model_params.initialize_weights()
embeddings = tf.nn.embedding_lookup(
weights["feature_embeddings"],
feature_idx
weights_first_order = tf.nn.embedding_lookup(
weights["weights_first_order"],
feature_idx
bias = weights['fm_bias']
#build function
##first order
first_order = tf.multiply(feature_values, weights_first_order)
first_order = tf.reduce_sum(first_order, 2)
first_order = tf.reduce_sum(first_order, 1, keepdims=True)
##second order
### feature * embeddings
f_e_m = tf.multiply(feature_values, embeddings)
### square(sum(feature * embedding))
f_e_m_sum = tf.reduce_sum(f_e_m, 1)
f_e_m_sum_square = tf.square(f_e_m_sum)
### sum(square(feature * embedding))
f_e_m_square = tf.square(f_e_m)
f_e_m_square_sum = tf.reduce_sum(f_e_m_square, 1)
second_order = f_e_m_sum_square - f_e_m_square_sum
second_order = tf.reduce_sum(second_order, 1, keepdims=True)
##final objective function
logits = second_order + first_order + bias
predicts = tf.sigmoid(logits)
##loss function
sigmoid_loss = tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels)
sigmoid_loss = tf.reduce_mean(sigmoid_loss)
loss = sigmoid_loss
#train op
if optimizer_used == 'adagrad':
optimizer = tf.train.AdagradOptimizer(
learning_rate=learning_rate,
initial_accumulator_value=1e-8)
elif optimizer_used == 'adam':
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
else:
raise Exception("unknown optimizer", optimizer_used)
train_op = optimizer.minimize(loss, global_step=tf.train.get_global_step())
#metric
eval_metric_ops = {
"auc": tf.metrics.auc(labels, predicts)
predictions = {"prob": predicts}

