官方文档 :
scipy.interpolate.interp1d
scipy.interpolate.interp1d(x, y, kind='linear', axis=-1, copy=True, bounds_error=None, fill_value=nan, assume_sorted=False)
其中,x 是一维数据;y 是 N 维数据且 y 在插值的方向轴上长度必须和 x 相等;kind 指定了插值类型(linear,nearest,zero,slinear,quadratic,cubic,previous,next),其中 zero,slinear,quadratic 和 cubic 指定了零、一、二、三阶样条插值;previous 和 next 仅仅返回当前点的前一个/后一个值。默认为 linear 线性插值。
from scipy.interpolate import interp1d
x = np.linspace(0, 10, num=11, endpoint=True)
y = np.cos(-x**2/9.0)
f = interp1d(x, y)
f2 = interp1d(x, y, kind='cubic')
xnew = np.linspace(0, 10, num=41, endpoint=True)
import matplotlib.pyplot as plt
plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')
plt.legend(['data', 'linear', 'cubic'], loc='best')
plt.show()
kind='linear(默认)':使用一次函数插值
x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/8)
y = np.sin(x)
tck = interpolate.splrep(x, y, s=0)
xnew = np.arange(0, 2*np.pi, np.pi/50)
ynew = interpolate.splev(xnew, tck, der=0)
plt.figure()
plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
plt.legend(['Linear', 'Cubic Spline', 'True'])
plt.axis([-0.05, 6.33, -1.05, 1.05])
plt.title('Cubic-spline interpolation')
plt.show()
x 和 y 是给定的一些坐标点,通过 splrep 函数计算出 B-spline 曲线的参数,再将该参数传递给 splev 函数计算出各个取样点 xnew 的插值结果。
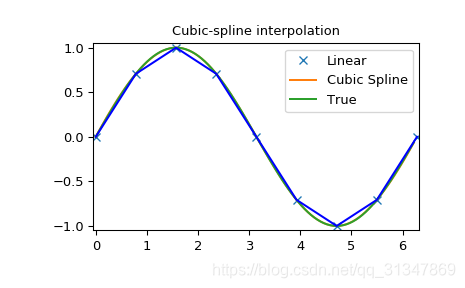
(xnew,sin(xnew)):实际 xnew 应该对应的 y 值,相当于 ground-truth(表示为图中绿色曲线)
官方文档 :scipy.interpolate.splrep
作用: 求取一维曲线的 B-spline 插值
给定一组数据点
k 次的光滑样条逼近。
scipy.interpolate.splrep(x, y, w=None, xb=None, xe=None, k=3, task=0, s=None, t=None, full_output=0, per=0, quiet=1)
其中,x 和 y 是点的横纵坐标,xb 和 xe 是间隔,k 为样条拟合度,建议使用三次样条(cubic splines),通常
import matplotlib.pyplot as plt
from scipy.interpolate import splev, splrep
x = np.linspace(0, 10, 10)
y = np.sin(x)
spl = splrep(x, y)
x2 = np.linspace(0, 10, 200)
y2 = splev(x2, spl)
plt.plot(x, y, 'o', x2, y2)
plt.show()
官方文档 :scipy.interpolate.splprep
scipy.interpolate.splprep(x, w=None, u=None, ub=None, ue=None, k=3, task=0, s=None, t=None, full_output=0, nest=None, per=0, quiet=1)
作用: 求取 N 维曲线的 B-spline 插值
phi = np.linspace(0, 2.*np.pi, 40)
r = 0.5 + np.cos(phi)
x, y = r * np.cos(phi), r * np.sin(phi)
from scipy.interpolate import splprep, splev
tck, u = splprep([x, y], s=0)
new_points = splev(u, tck)
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.plot(x, y, 'ro')
ax.plot(new_points[0], new_points[1], 'r-')
plt.show()
x:列表类型 [x,y],x 和 y 分别是表示曲线上坐标点的横纵坐标
w:数组类型,长度与 x[0] 相同,默认为 ones(len(x[0]))
k:spline 等级,推荐使用 Cubic splines(k=3),默认为 3
s:float 类型,平滑条件,较大的 s 意味着曲线比较光滑,建议 s 的取值在
官方文档:/tutorial/interpolate插值,即依据一系列点 (x,y)(x,y)(x,y) 通过一定的算法找到一个合适的函数来逼近这些点,反映出这些点的走势规律。当拟合出插值函数后便可用这个插值函数计算其他 xxx 对应的的 yyy 值,这就是插值的意义所在。interpolate.interp1d官方文档 :scipy.interpolate.interp1d语法:sci...
1.插值
scipy.
interpolate
SciPy的
interpolate模块提供了许多对数据进行插值运算的函数,范围涵盖简单的一维插值到复杂多维插值求解。
一维插值:当样本数据变化归因于一个独立的变量时;
多维插值:反之样本数据归因于多个独立变量时。
注:一维插值这里就不再讲述了,主要是对二维插值的一个总结。
2.
interp2d()
from
scipy.
interpolate import
interp2d
interp2d(x,y,z,kind='linear')
这里有几个注意事项:
#p100下半部分
#4.1.2scipy
#例子2 interpolate.splev 函数 利用B样条和它的导数进行插值,interpolate.splev课展现二维曲线插值
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
from scipy.interpolate import spl
scipy.interpolate.interp2d注意事项python插值方法scipy.interpolate.interp2d注意事项问题scipy.interpolate.interp2d的使用变化说明
python插值方法scipy.interpolate.interp2d注意事项
在使用scipy.interpolate.interp2d对数据插值时,发现输出的数据图像并不相同,然后找了一下原因。
坐标用的是经纬度数据,粗细的纬度数据都是从60~-60这样排列的,原因应该就是插值完的输出坐
完整教程下载地址:http://forum.armfly.com/forum.php?mod=viewthread&tid=45785
第18章 附件C---波形拟合
emWin5.44中新增的样条函数Spline可以实现波形拟合,即波形插补。不过当前可用于芯片的emWin库还没有升级到5.44,等升级到5.44后,大家可以做研究。
下面知识点来自百度百科...
class scipy.interpolate.interp1d(x, y, kind='linear', axis=-1, copy=True, bounds_error=None, fill_value=nan, assume_sorted=False)
import numpy as np
import matplotlib.pyplot as plt
from scipy imp...
from
scipy import
interpolate
import matplotlib as mpl
mpl.rcParams["font.sans-serif"] = ["SimHei"]
mpl.rcParams["axes.unicode_min...
