HorNet: Efficient High-Order Spatial Interactions with Recursive Gated Convolutions
Q1论文试图解决什么问题?
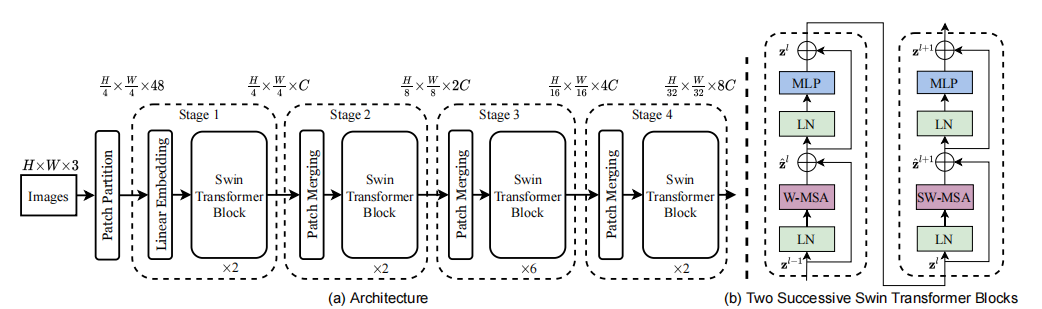
计算机视觉任务中,Transformer 的Block设计一般遵循一个 meta architecture,如下图所示。虽然 token mixer 的类型会有不同 (Self-attention,Spatial MLP,Window-based Self-attention 等),但是基本的宏观架构相同。

目前很多工作的出发点都是从不同的角度改进token mixer,本文从 显式地建模高阶的相互作用 的角度出发,提升模型的表达能力。
Q2这是否是一个新的问题?有哪些相关研究?
否。
vision transformer提出的这个结构,token mixer使用的是多头自注意力。

swin transformer 中使用的是shifted-windows多头自注意力。
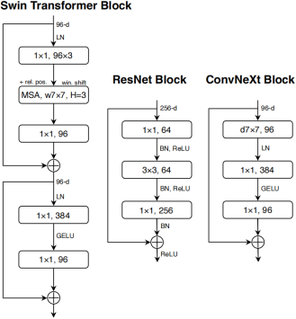
ConvNeXt基于此结构,并结合 7×7 的 Depth-wise Convolution 构建了一系列高性能的 CNN 架构。
GFNet基于此结构,并结合 2D-FFT 的傅里叶变换和 2D-IFFT 的反变换构建了一系列高性能的通用 Backbone 架构。

RepLKNet基于此结构,并结合 31×31 的超大核卷积操作以及结构重参数化的方案构建了一系列高性能的通用 Backbone 架构。
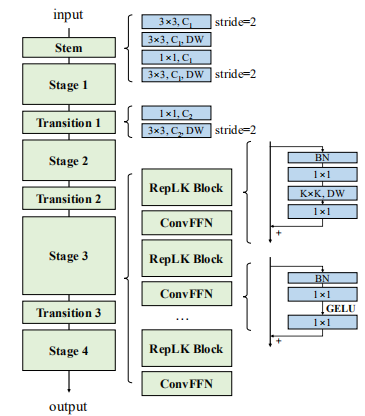
VAN基于此结构,从改进大核卷积的角度出发,将大核卷积分解成depth-wise卷积、膨胀率为d的depth-wise卷积核一个1x1卷积。
Q3论文中提到的解决方案之关键是什么?
动机
作者把视觉 Transformer 成功的关键因素归结为动态权重 (指的是 attention 矩阵的值与具体的输入有关,input-adaptive),长距离建模 (long-range) 和高阶的空间交互 (high-order)。
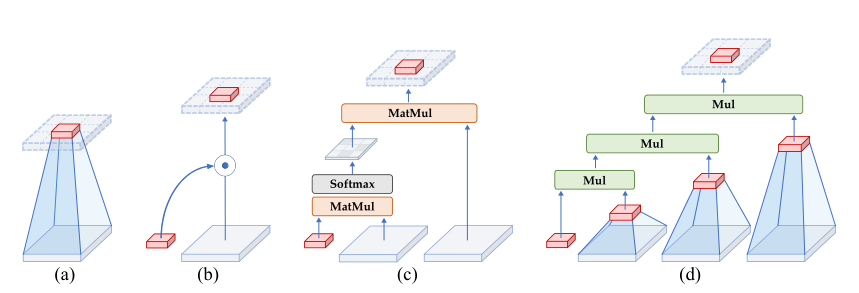
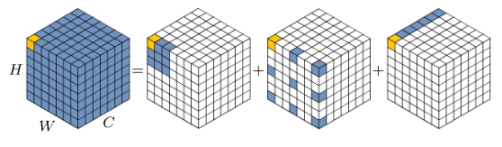
图a,普通卷积运算没有显式地考虑空间位置(即红色特征)与其相邻区域(即浅灰色区域)之间的空间相互作用。
图b,增强的卷积运算,如动态卷积,通过生成动态权值引入显式的空间相互作用。
图c,transformer中的点积自注意操作由两个连续的空间交互组成,通过在Q、K、V之间执行矩阵乘法。
图d,本文所提出的递归门控卷积。可以实现更高阶的空间交互。
优点:
1)高效。基于卷积的实现避免了自注意的二次复杂度。在执行空间交互过程中逐步增加通道宽度的设计可以使模型实现有限复杂性的高阶交互。
2)可扩展。将自注意中的二阶相互作用扩展到任意阶,进一步提高了建模能力。由于没有对空间卷积的类型做假设, g^n Conv兼容各种内核大小和空间混合策略,如深度卷积和全局滤波器模块。
3) 平移不变。 g^n Conv充分继承了标准卷积的平移不变性,为主要视觉任务引入了有益的归纳偏差,避免了局部注意带来的不对称。
使用 g Conv实现一阶的空间交互
递归的门控卷积的基本操作是 g Conv,设输入特征为 X\in R^{HW×C} ,门控卷积的输出可以写成:
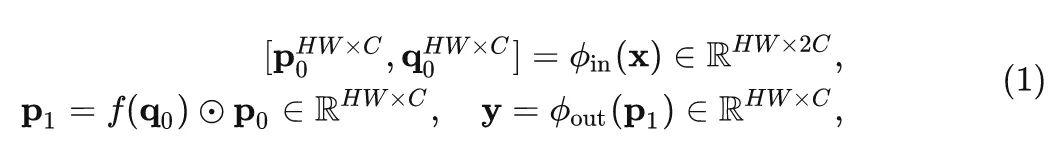
式中, \phi_{in} 和 \phi_{out} 使用1x1卷积将通道数翻倍。 f 是 depth-wise 的卷积(也可以使用GFNet中的全局滤波器模块可以带来更好的实验效果,因为全局过滤器捕获的全局交互有助于性能提升)
上式可以认为是 p_0 及其周边特征 q_0 的1阶相互作用。
使用 g^n Conv实现高阶的空间交互
接下来递归的使用 g Conv来实现长距离建模和高阶的空间交互。
首先通过 \phi_{in} 得到一系列的投影特征 p_0 和 \left\{ {q_k} \right\}_{k=0}^{n-1} ,对应其通道数分别为 C_0 - C_{n-1} ,n为阶数。

再以递归的方式进行门控卷积:

式中, 每次递归的过程除以 \alpha 是为了稳定训练, \left\{ f_k \right\} 是一系列的 Depth-wise 卷积操作, \left\{ g_k \right\} 是1x1卷积,用来在每次递归的过程匹配 p_k 和 q_k 的通道数。

将最后一次递归的输出 q_n 输入到 \phi_{out} 得到 g^n Conv的结果。这样就实现了某一特征和其周边特征的n阶相互作用。
但是要计算式3,就需要计算 f_k(q_k),k=0,1,...,n-1 ,这一步其实不需要算 n 次,而是可以通过直接将组合的特征 \left\{ {q_k} \right\}_{k=0}^{n-1} 通过一个 Depth-wise Convolution 来完成,这可以在 GPU 上进一步简化实现, 提高效率。
为了确保高阶交互不会引入太多的计算开销,作者将每一阶的通道维度设置为指数递减的形式:


g^n Conv计算复杂度分析
可分为3部分。
第一步和最后一步的 \phi_{in} 和 \phi_{out} :
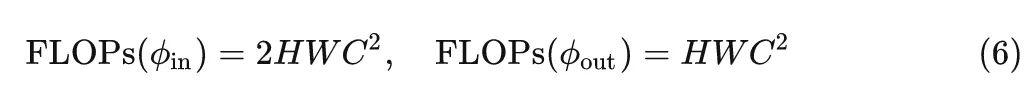
Depth-wise卷积 f
卷积核大小为K的Depth-wise 卷积作用在特征 \left\{ {q_k} \right\}_{k=1}^{n-1} 上面,其中, q_k{\in}R^{HW×C_k},C_k = \frac{C}{2^{n-k-1}} :
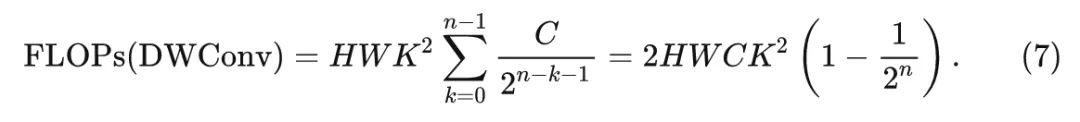
维度匹配 \left\{ g_k \right\} 的计算量:

因此, 总的计算量是:

g^n Conv代码
关于Depth-wise卷积的实现,作者使用了两种形式:一种是ConvNeXt中的7x7Depth-wise卷积,一种是GFNet中所使用的global filter:用可学习的global filter对频域特征进行乘法运算,相当于在具有全局核大小和圆形填充的空间域中进行卷积。作者使用global filter的修改版本,使用global filter处理一半通道,使用3×3深度卷积处理另一半通道。
def get_dwconv(dim, kernel, bias):
return nn.Conv2d(dim, dim, kernel_size=kernel, padding=(kernel-1)//2 ,bias=bias, groups=dim)
class GlobalLocalFilter(nn.Module):
def __init__(self, dim, h=14, w=8):
super().__init__()
self.dw = nn.Conv2d(dim // 2, dim // 2, kernel_size=3, padding=1, bias=False, groups=dim // 2)
self.complex_weight = nn.Parameter(torch.randn(dim // 2, h, w, 2, dtype=torch.float32) * 0.02)
trunc_normal_(self.complex_weight, std=.02)
self.pre_norm = LayerNorm(dim, eps=1e-6, data_format='channels_first')
self.post_norm = LayerNorm(dim, eps=1e-6, data_format='channels_first')
def forward(self, x):
x = self.pre_norm(x)
x1, x2 = torch.chunk(x, 2, dim=1)
x1 = self.dw(x1)
x2 = x2.to(torch.float32)
B, C, a, b = x2.shape
x2 = torch.fft.rfft2(x2, dim=(2, 3), norm='ortho')
weight = self.complex_weight
if not weight.shape[1:3] == x2.shape[2:4]:
weight = F.interpolate(weight.permute(3,0,1,2), size=x2.shape[2:4], mode='bilinear', align_corners=True).permute(1,2,3,0)
weight = torch.view_as_complex(weight.contiguous())
x2 = x2 * weight
x2 = torch.fft.irfft2(x2, s=(a, b), dim=(2, 3), norm='ortho')
x = torch.cat([x1.unsqueeze(2), x2.unsqueeze(2)], dim=2).reshape(B, 2 * C, a, b)
x = self.post_norm(x)
return xg^n Conv代码
class gnconv(nn.Module):
def __init__(self, dim, order=5, gflayer=None, h=14, w=8, s=1.0):
super().__init__()
self.order = order
self.dims = [dim // 2 ** i for i in range(order)]
self.dims.reverse()
self.proj_in = nn.Conv2d(dim, 2*dim, 1)
if gflayer is None:
self.dwconv = get_dwconv(sum(self.dims), 7, True)
else:
self.dwconv = gflayer(sum(self.dims), h=h, w=w)
self.proj_out = nn.Conv2d(dim, dim, 1)
self.pws = nn.ModuleList(
[nn.Conv2d(self.dims[i], self.dims[i+1], 1) for i in range(order-1)]
self.scale = s
print('[gnconv]', order, 'order with dims=', self.dims, 'scale=%.4f'%self.scale)
def forward(self, x, mask=None, dummy=False):
B, C, H, W = x.shape
fused_x = self.proj_in(x)
pwa, abc = torch.split(fused_x, (self.dims[0], sum(self.dims)), dim=1)
dw_abc = self.dwconv(abc) * self.scale
dw_list = torch.split(dw_abc, self.dims, dim=1)
x = pwa * dw_list[0]
