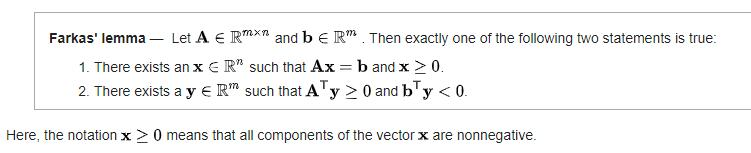【Gurobi】针对优化模型Infeasible的错误，如何快速Debug?_model is infeasible_王源WANGYuan的博客

1 你是否遇到过 Infeasible model 的问题？

相信用Gurobi写过model的童鞋大概率会遇到一个bug 就是当你好不容易把模型输入到gurobi里边后，当你运行程序让gurobi去优化求解你的问题的时候，gurobi 却报出一个 infeasible model 的错误信息。此时有两种可能性第一个原因是你建立的模型本身是有问题的，导致你的模型里的约束条件有互相矛盾的地方，所以这个模型根本就没有可行解；第二个原因是你的模型本身没有问题，只不过你在把数学模型输入到gurobi的过程中编程错误或者参数值输入不正确导致你的模型不可行了。
这篇文章主要说一下针对第二种原因的处理办法，如何快速找到是哪些约束之间互相矛盾造成模型不可行的。话说总不能一个一个约束用眼睛用手去算去对吧。好在gurobi给我们提供了一个强大的函数computeIIS()能够迅速帮我们锁定出是有问题的约束条件。

2 computeIIS()的用法

话不多说直接用一个例子来说明，computeIIS()的用法（代码运行环境为python 3.6，gurobi 9.0.0）

import gurobipy as gp
m = gp.Model ("LP Model")
x = m.addVars(2, lb = 0.0, ub = 1.0, name = 'x')
m.addConstr(x[0] + x[1] >= 1.2, "c1")
m.addConstr(x[0] + x[1] <= 1.1, "c2")
m.addConstr(x[0] + x[1] >= 0.1, "c3")
m.setObjective(x[0] + 2*x[1])
m.optimize()
m.computeIIS()
m.write("model1.ilp")
从上面的代码容易看到第一条约束x0+x1>=1.2和第二条约束x0+x1<=1.1是互相矛盾的，因此该模型不存在可行解。所以当我们求解这个模型的时候，gurobi会报出 infeasible model 的错误信息，此时我们可以调用computeIIS()即可得到哪些约束是互相矛盾的，即去掉这些矛盾约束剩下的约束构成的问题是可行的。
 为了方便观察computeIIS()的输出结果，可以用m.write(“model1.ilp”)输出一个扩展名魏".ilp"的文件，里边会包含所以矛盾的约束，针对上面的例子生成的ilp文件内容如下所示： 
Minimize
Subject To
 c1: x[0] + x[1] >= 1.2
 c2: x[0] + x[1] <= 1.1
Bounds
 x[0] free
 x[1] free
可以看到确实是输出了前2个造成矛盾的约束，而第三个约束没有矛盾所以没有输出在.ilp文件内。那么这里只是举了一个非常简单的例子来说明computeIIS()的用法，实际问题所构成的优化模型往往是非常复杂的，成千上万条约束依靠人工方式去排查哪些约束有问题是非常困难的。此时如果能采用computeIIS()输出有问题的约束，对于我们debug来说无疑是非常高效的一个小技巧。 
3 computeIIS() 的局限性
 
computeIIS()功能这么强大可以很快找出互相矛盾的约束，那是不是它就是一个很完美的解决我们矛盾约束的方法呢？在实际问题中computeIIS()并不是万能的。这是因为如果你的问题约束数量稍微多一点的话，computeIIS()所耗费的时间是非常长的，也就是说在大多数实际问题中我们很能直接采用computeIIS()去找到矛盾约束，因为计算时间太长了。 
那么此时我们不得不采用一些“土”办法来初步定位出可能出问题的约束在哪类约束里边，例如我们可以注释掉一部分约束，然后运行程序，如果程序没有报出infeasible的提示，就表明这部分被注释掉的约束里边含有矛盾的约束。通过这个方法可以初步定位出可能有问题的约束，然后在小范围内再使用computeIIS()去精确定位是一个不错的选择。总之在实际问题中，我们需要灵活的去处理，computeIIS()有一定的作用，但它并不是解决infeasible 的万能钥匙。 
4 采用 Farkas lemma帮助判断模型是否可行
 
如果仅仅想掌握技巧但对computeIIS()背后原理不感兴趣的童鞋可以直接跳过本节。
 如果我们稍微好奇一下，怎么用算法来判断出一个优化问题是否有可行解，即computeIIS()这个函数背后的算法是什么。其实这个问题并不陌生，如果对线性规划学习稍微深入一点的童鞋，一定学过一个Farkas lemma 。Farkas lemma的具体形式如下所示：
 
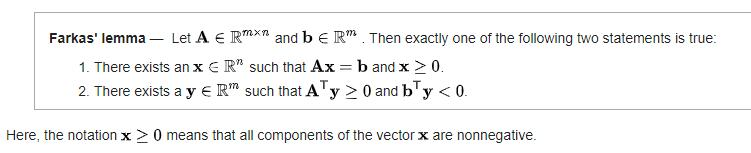
 简单来说，命题1和命题2 有且只能有一个是成立的。若命题1成立，则命题2一定不成立，若命题2成立，则命题1一定不成立。
 Farkas lemma的作用就是 可以让命题1和命题2互相转化，如果我要证明命题1成立 我可以去证明命题2不成立，反之亦然。看到这里大家大致已经能猜到了，computeIIS()背后的原理一定是 Farkas lemma，具体内容可参考文献[1]。
 所以最后我想说的是初学 Farkas lemma，虽然我能看懂整个推导过程，但是我不知道为啥要证明这个引理，这个引理到底有什么用？直到当你积累大量的经验后，你方才能领悟到 Farkas lemma的妙处。 
参考文献：
 [1] John Gleeson, Jennifer Ryan, (1990) Identifying Minimally Infeasible Subsystems of Inequalities. ORSA Journal on Computing, 2(1):61-63.
 [2] How does Gurobi compute the IIS for infeasible models?
 [3] 维基百科 Farkas lemma
                                    用 cplex 或 gurobi 构建数学规划模型时，要是求解变量或约束条件比较多，刚开始总是不成功的，经常会遇到模型非可行的情况。一般是由于约束条件输入错误导致的，但是具体哪一个约束条件呢？一个一个核实太麻烦了。
发现 cplex 或者 gurobi 都提供了寻找非可行原因的一些类和方法。
                                    自学Gurobi的时候发现国内缺乏相对应的教程，大多止于浅层的gurobi安装和搭载，稍微深入点也只是最基础的模型建立：add variable, update, add constraint, set objective, optimize 和基本的读写。 甚至缺乏对于结果的解读。
Google到的内容比 百度 多的多。
最好的资料当然是官网的 http://www.gurobi.com/d...
                                    gurobi与python应用2指南见refman，或者google进gurobi官网借助翻译软件为中文1.定义变量2.约束部分
指南见refman，或者google进gurobi官网借助翻译软件为中文
1.定义变量
常见的定义变量是:
m.addvars()
// An highlighted block
addVars ( *indices, lb=0.0, ub=float(’inf’), obj=0.0, vtype=GRB.CONTINUOUS,
name="" );
默认下界为0。
当下界比0
                                    python +gurobipy数学建模
最近帮人做了一个混合整数线性规划case,使用了gurobipy优化库。学术版官网可以直接申请licence，三个月有效然后可以继续申请。总比要收费的cplex好点哈哈。但是还是遇到了一些坑，现在把整个问题与解决方案，代码，遇到的坑都记录一下。
对比cplex,gurobipy更适合复现一个优化问题，因为gurobipy不用把优化问题写成矩阵相乘的标准形式而是直接堆公式就行。
比如二次规划，不用写成：
XTQX + A*X的形式而是直接可以循环定义目标函数