三次样条（cubic spline）插值

3 年前 · 来自专栏自动驾驶系列学习笔记

阿贵

在西安上学

当已知某些点而不知道具体方程时候，最经常遇到的场景就是做实验，采集到数据的时候，我们通常有两种做法：拟合或者插值。拟合不要求方程通过所有的已知点，讲究神似，就是整体趋势一致。插值则是形似，每个已知点都必会穿过，但是高阶会出现龙格库塔现象，所以一般采用分段插值。今天我们就来说说这个分段三次样条插值。

顾名思义，分段就是把区间[a,b]分成n个区间 [(x_0,x_1),(x_1,x_2),\dots,(x_{n-1},x_n)] ,共有n+1个点，其中两个端点 x_0=a,x_n=b 。三次样条就是说每个小区间的曲线是一个三次方程，三次样条方程满足以下条件：

1，在每个分段小区间 [x_i,x_{i+1}] 上， S(x)=S_i(x) 都是一个三次方程

2，满足插值条件，即 S(x_i)=y_i \quad (i=0,1,...,n)

3, 曲线光滑，即 S(x)，S'(x)，S''(x) 连续

则这个三次方程可以构造成如下形式：

y=a_i+b_ix +c_ix^2 +d_i x^3 这种形式,我们称这个方程为三次样条函数 S_i(x) 。

从 S_i(x) 可以看出每个小区间有四个未知数（a_i,b_i,c_i,d_i），有n个小区间，则有4n个未知数，要解出这些未知数，则我们需要4n个方程来求解。

求解

我们要找出4n个方程来求解4n个未知数

首先，由于所有点必须满足插值条件， S(x_i)=y_i \quad (i=0,1,...,n) ，除了两个端点，所有n-1个内部点的每个点都满足 S_i(x_{i+1})=y_{i+1} \quad S_{i+1}(x_{i+1})=y_{i+1} 前后两个分段三次方程，则有2(n-1)个方程，再加上两个端点分别满足第一个和最后一个三次方程，则总共有2n个方程；

其次，n-1个内部点的一阶导数应该是连续的，即在第 i 区间的末点和第 i+1 区间的起点是同一个点，它们的一阶导数应该也相等，即 S'_{i}(x_{i+1})=S'_{i+1}(x_{i+1}) 则有n-1个方程

另外，内部点的二阶导数也要连续，即 S''_{i}(x_{i+1})=S''_{i+1}(x_{i+1}) ,也有n-1个方程

现在总共有4n-2个方程了，还差两个方程就可以解出所有未知数了，这两个方程我们通过边界条件得到。

有三种边界条件：自然边界，固定边界，非节点边界

1，自然边界 ( Natural Spline )：指定端点二阶导数为0， S''(x_0)=0=S''(x_n)

2, 固定边界 ( Clamped Spline ): 指定端点一阶导数，这里分别定为A和B。即 S'_0(x_0)=A,\quad S'_{n-1}(x_n)=B

3, 非扭结边界( Not-A-Knot Spline ): 强制第一个插值点的三阶导数值等于第二个点的三阶导数值，最后第一个点的三阶导数值等于倒数第二个点的三阶导数值. 即 S'''_0(x_0)=S'''_1(x_1) \quad and \quad S'''_{n-2}(x_{n-1})=S'''_{n-1}(x_n)

具体推导

\begin{aligned} S_{i}(x) &=a_{i}+b_{i}\left(x-x_{i}\right)+c_{i}\left(x-x_{i}\right)^{2}+d_{i}\left(x-x_{i}\right)^{3} \\ S_{i}^{\prime}(x) &=b_{i}+2 c_{i}\left(x-x_{i}\right)+3 d_{i}\left(x-x_{i}\right)^{2} \\ S_{i}^{\prime \prime}(x) &=2 c_{i}+6 d_{i}\left(x-x_{i}\right) \end{aligned}

1, 由 S_{i}(x_{i})=a_{i}+b_{i}\left(x_i-x_{i}\right)+c_{i}\left(x_i-x_{i}\right)^{2}+d_{i}\left(x_i-x_{i}\right)^{3}=y_{i}

可得 a_i=y_i

2，用 h_{i}=x_{i+1}-x_{i} 表示步长，由 S_i(x_{i+1})=y_{i+1} 推出 a_{i}+h_{i} b_{i}+h_{i}^{2} c_{i}+h_{i}^{3} d_{i}=y_{i+1}

3,由 S'_{i}(x_{i+1})=S'_{i+1}(x_{i+1}) 推出

\begin{array}{l}{S_{i}^{\prime}\left(x_{i+1}\right)=b_{i}+2 c_{i}\left(x_{i+1}-x_{i}\right)+3 d_{i}\left(x_{i+1}-x_{i}\right)^{2}=b_{i}+2 c_{i} h+3 d_{i} h^{2}} \\ {S_{i+1}^{\prime}\left(x_{i+1}\right)=b_{i+1}+2 c_{i}\left(x_{i+1}-x_{i+1}\right)+3 d_{i}\left(x_{i+1}-x_{i+1}\right)^{2}=b_{i+1}}\end{array}

可得

b_{i}+2 h_{i} c_{i}+3 h_{i}^{2} d_{i}=b_{i+1}

4，由 S''_{i}(x_{i+1})=S''_{i+1}(x_{i+1}) 推出 2 c_{i}+6 h_{i} d_{i}=2 c_{i+1}

设 \boldsymbol{m}_{i}=\boldsymbol{S}_{i}^{\prime \prime}\left(\boldsymbol{x}_{i}\right)=2 \boldsymbol{c}_{i} 则 2 c_{i}+6 h_{i} d_{i}=2 c_{i+1} 改写为 m_{i}+6 h_{i} d_{i}=m_{i+1}

可得

d_{i}=\frac{m_{i+1}-m_{i}}{6 h_{i}}

5，现在 a_i,c_i,d_i 都可以表示成二阶导的关系式，将其代入到 a_{i}+h_{i} b_{i}+h_{i}^{2} c_{i}+h_{i}^{3} d_{i}=y_{i+1} 可得

b_{i}=\frac{y_{i+1}-y_{i}}{h_{i}}-\frac{h_{i}}{2} m_{i}-\frac{h_{i}}{6}\left(m_{i+1}-m_{i}\right)

6，将 a_i,b_i,c_i,d_i 代入 b_{i}+2 h_{i} c_{i}+3 h_{i}^{2} d_{i}=b_{i+1} 可得

h_{i} m_{i}+2\left(h_{i}+h_{i+1}\right) m_{i+1}+h_{i+1} m_{i+2}=6\left[\frac{y_{i+2}-y_{i+1}}{h_{i+1}}-\frac{y_{i+1}-y_{i}}{h_{i}}\right]

这样我们可以构造一个以m为未知数的线性方程组。

1）在自然边界条件时， m_0=0\quad m_n=0

可以看出，左侧的系数矩阵为 严格对角占优矩阵 。即：每一行中对角元素的值的模 > 其余元素值的模之和。故线性方程组有唯一解，且雅克比迭代法、高斯-赛德尔迭代法和0<ω≤1的超松弛迭代法均收敛。

2）在夹持边界条件时，

\begin{aligned} S_{0}^{\prime}\left(x_{0}\right)=A & \Longrightarrow \quad b_{0}=A \\ & \Longrightarrow A=\frac{y_{1}-y_{0}}{h_{0}}-\frac{h_{0}}{2} m_{0}-\frac{h_{0}}{6}\left(m_{1}-m_{0}\right) \\ & \Longrightarrow 2 h_{0} m_{0}+h_{0} m_{1}=6\left[\frac{y_{1}-y_{0}}{h_{0}}-A\right] \end{aligned}

\begin{array}{l}{S_{n-1}^{\prime}\left(x_{n}\right)=B \quad \Rightarrow \quad b_{n-1}=B} \\ {\quad \Rightarrow \quad h_{n-1} m_{n-1}+2 h_{n-1} m_{n}=6\left[B-\frac{y_{n}-y_{n-1}}{h_{n-1}}\right]}\end{array}

将上述两个公式带入方程组，新的方程组左侧为

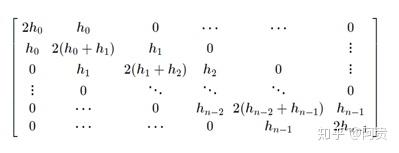
3）在非扭结边界条件时，

\begin{array}{l}{S_{0}^{\prime \prime \prime}\left(x_{0}\right)=S_{1}^{\prime \prime \prime}\left(x_{1}\right)} \\ {S_{n-2}^{\prime \prime \prime}\left(x_{n-2}\right)=S_{n-1}^{\prime \prime \prime}\left(x_{n-1}\right)}\end{array}

由于

S_{i}^{\prime \prime \prime}(x)=6 d_{i} ，并且 d_{i}=\frac{m_{i+1}-m_{i}}{6 h_{i}}

d_0=d_1 \quad d_{n-2}=d_{n-1}

即

\begin{array}{l}{h_{1}\left(m_{1}-m_{0}\right)=h_{0}\left(m_{2}-m_{1}\right)} \\ {h_{n-1}\left(m_{n-1}-m_{n-2}\right)=h_{n-2}\left(m_{n}-m_{n-1}\right)}\end{array}

新的方程组系数矩阵可写为：