python数据分析【一】Numpy快速入门

未曾优秀也未放弃

坐着总比躺着好

如果说你想学习或者刚刚开始数据分析工作，Numpy是一个强烈推荐给你的工具库。

1 numpy简介

numpy，pandas，scipy 是python三大科学计算库，而后两者是基于numpy库的扩展和补充。简单聊聊为什么numpy强大？

强大的n维数组对象-ndarray，它是一系列"同类型数据"的集合
numpy是Python的一个扩展程序库，支持数组与矩阵运算
支持广播运算，运算速度极快

引用菜鸟教程的解释：

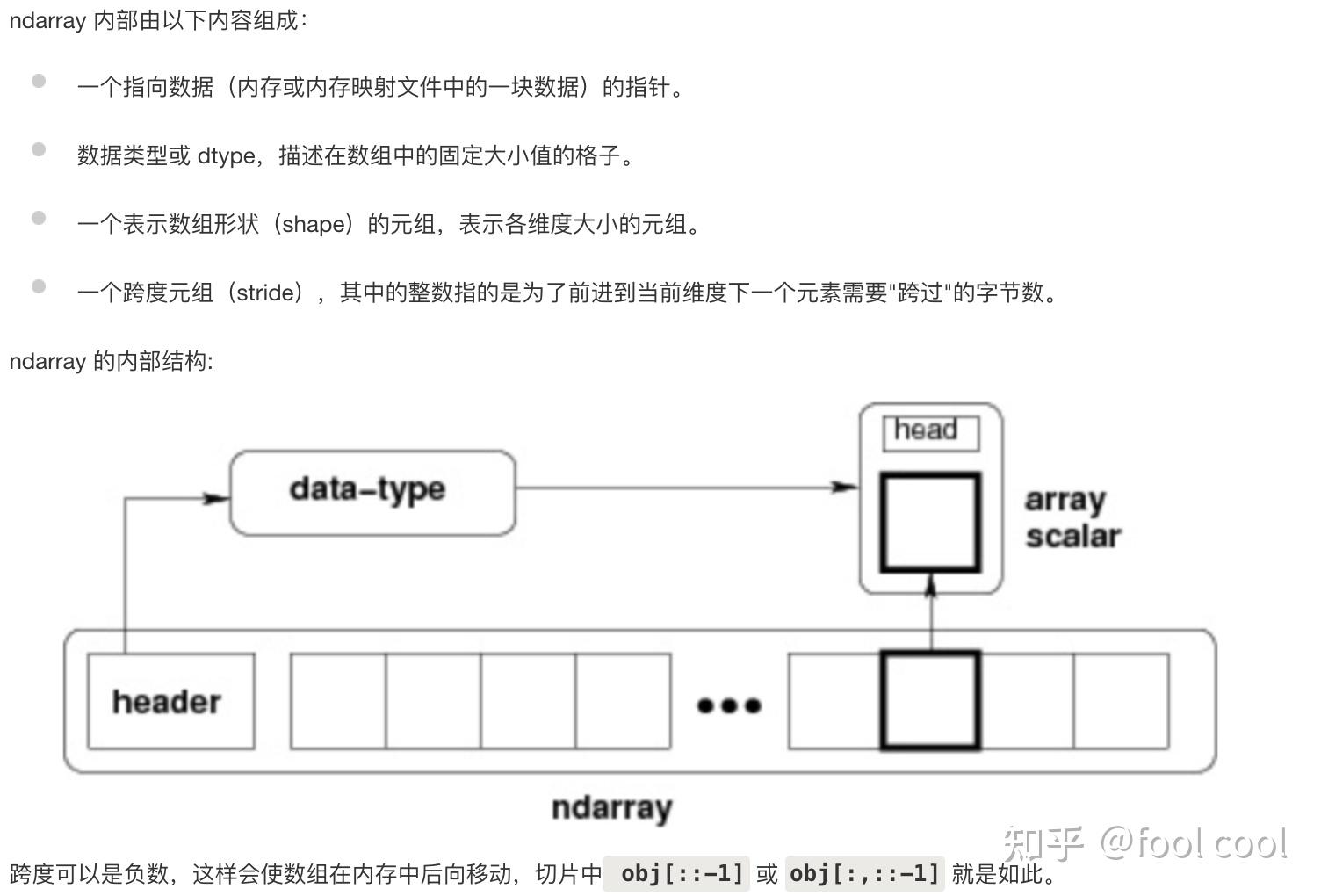
2 数组创建

import numpy as np 导包
Help on built-in function array in module numpy:
array(...)
    array(object, dtype=None, *, copy=True, order='K',
          subok=False, ndmin=0, like=None)
    Create an array.
    Parameters
    ----------
    object : array_like
        An array, any object exposing the array interface, an object whose
        __array__ method returns an array, or any (nested) sequence.
    dtype : data-type, optional
        The desired data-type for the array.  If not given, then the type will
        be determined as the minimum type required to hold the objects in the
        sequence.

上面是np.array()的的帮助文档。

numpy.array(object, dtype = None, copy = True, order = None, subok = False, ndmin = 0)

2.1 经典数组生成

lst = [1, 2, 3]
a = 12
array = [[1,2,3], [4,5,6]]
display(np.array(a))
display(np.array(lst))
display(np.array(lst, ndim=2))  # 设置成两个维度
np.array(array)

2.2 特殊数组生成

np.zeros(shape) 快速生成全为0的数组，shape表示形状，例如3行四列；ones则是快速生成全为1的数组。
np.full(shape, fill_value) 用fill_value填充指定的数组形状

ones = np.ones(shape=[3),
zeros = np.zeros(shape=[3, 2])
fulls = np.full(shape = [2,3], fill_value=2)
# ones 和 zeros 可以用于快速增加一列或者一行
display(ones, zeros)

2.3 随机数组生成

在模拟练习的时候，总不能全拿0和1的数组来练习吧，这也太够逼真了，因此介绍一写快捷生成数据的方法。

random_0_to_1 = np.random.random(size=3) 
# 0-1均匀分布
# Return random floats in the half-open interval [0.0, 1.0)
rdm1 = np.random.randint(low=0, high=10, size=3)
# Return random integers from `low` (inclusive) to `high` (exclusive)
rdm2 = np.random.randn(3) # 标准正态分布
# Return a sample (or samples) from the "standard normal" distribution.
noraml = np.random.normal(loc=10, scale=2, size=5)  
# 均值为loc，标准差为sclae，生产size个数字
# Draw random samples from a normal (Gaussian) distribution.
display(random_0_to_1, rdm1, rdm2, noraml)

2.4 规律数组生成

np.arange(start, stop, step) 和range()类似，左闭右开，默认起始从0开始，步长默认为1
比如你只想要0到10的一维数组

t = np.arange(11)
Values are generated within the half-open interval [start, stop)
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10])

比如你只要0到10的偶数

t = np.arange(0, 11, 2)
array([ 0,  2,  4,  6,  8, 10])

np.linspace(start, stop, num) 规定起始位置（闭区间），要多少个数据（num）

np.linspace(0, 1, 9)
# 0开始，1结束，需要9个数据，即8个间隔，1/8=0.125
# array([0.   , 0.125, 0.25 , 0.375, 0.5  , 0.625, 0.75 , 0.875, 1.   ])

3 数组属性

nd = np.random.randint(1,50, (2,3))
array([[10,  5,  5],
       [14,  7, 18]])

3.1 查看属性

ndarray数组维度 nd.ndim，表示这个数组有几个维度，2维就类似x，y轴

nd.ndim. 
# 2

ndarray数组形状

表示数组形状，简单说就是几行几列，在三维或者更高维度就涉及到面的方向了

nd.shape. # (2,3)

ndarray数组数据类型

表示数组中的元素是什么数据类型，在numpy中不同的数据类型占有内存大小不同

int类型默认为int64类型

nd.dtypes
# dtype('int64')

ndarray数组元素个数

表示数组有多少个元素，起始就等于shape中各个元素的乘积

nd.size
# 6

ndarray数组每个元素的内存大小（以字节为单位）

因为前面提及了数据类型为int64，一个字节8比特位，64/8=8 字节

nd.itemsize  # 8

3.2 修改属性

np.reshape() 更改数组形状

前面nd的形状是2行3列，现在我们可以把它改成3行2列， 前提条件是改前和改后shape中的元素乘积相等

nd.reshape(3,2)
array([[10,  5],
       [ 5, 14],
       [ 7, 18]])
"""

Np.dtype 数组元素的数据类型

nd.dtype = np.float32
nd.dtype  # np.float32

np.astype(type) 数据类型转换

nd2 = nd.astype('int32') nd2

4 广播机制（broadcast）

广播允许通用功能以有意义的方式处理不具有完全相同形状的输入。

举个例子，一维数组有3个元素，你让它 + 3，它是怎么实现的呢？我们都知道如果是位置一一对应那肯定可以的。

再举个例子，一个2x3的数组，让它与一维数组shape=（2，）相加，它又应该怎么实现呢？

直接看代码案例

nd = np.arange(6).reshape(2,3)
print(nd)
[[0, 1, 2],
 [3, 4, 5]]
nd2 = np.arange(3)
print(nd2)
# [0, 1, 2]
print(nd2 + 3)
print('-'*30)
print(nd + nd2)
'''[3 4 5]
------------------------------
[[0 2 4]
 [3 5 7]]'''

肉眼可见啊，一维数组nd2 [0, 1, 2] + 3 是沿着一个轴方向，每个元素都加3；

而二维数组nd 加上一维数组nd2， 则是每一行（一个轴方向）分别与nd2对应位置的元素相加 。

总结：当数组形状不完全一致时，如果两个数组只要有一个维度对应的形状（shape）相同（n对1也算相同），便可以进行运算，它会采取广播机制，也就是复制填充到对应位置，然后进行运算。

这里用上官方的详细的图文解释

Figure1表示，一维数组与仅有一个元素的数组相加，我们可以理解为他们的高度方向都是1，满足某个维度下的形状相同，因此元素可以朝着另一个维度复制填充，最合进行运算。也就是a 每个元素都 + 3

Figure2表示，二维数组与一维数组相加，我们可以理解为a是竖直维度为 4，水平维度为3的形状，而b是竖直维度为1，水平维度3，两者的水平维度形状相同，因此可以在竖直维度进行复制填充（复制水平维度元素）最后进行运算。也就是a 每个元素都都对应的加上 [1, 2, 3]

Figure3表示，二维数组 a 与一维数组 b相加，我们可以理解为a是竖直维度为 4，水平维度为1，而b是竖直维度为1，水平维度3。a相对b而言水平维度形状更小，而遇见了1 与 n对应，都可以进行广播，因此a先在水平维度复制着自己，反之b相对a而言则是在竖直方向上复制。

简言之：对应维度形状大小相同才能进行广播运算，1是例外，因为某个维度下为1的形状可以随便填充啊，知道和对方形状一致。

5 索引与切片

5.1 一维数组

一维的数组可以进行索引、切片和迭代操作的，就像列表和其他Python序列类型一样。

a = np.arange(10)
a[1]   # 1
a[::2] # [0, 2, 4, 6, 8]
a[::-1] # 倒序 [9, 8, 7, 6, 5, 4, 3, 2, 1, 0]

5.2 二维数组

多维的数组每个轴可以有一个索引。 不同轴方向的索引以逗号分隔的元组 给出：

a = np.arange(16).reshape(4,4)
"""[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]
 [12 13 14 15]]"""
a[0, 1] # 第一行第二列 1
a[-1,-1] # 最后一行最后一列 15
a[:, -2] # 所有行的倒数第二列 [ 2,  6, 10, 14]
a[:, :2] # 所有行 前两列
'''array([[ 0,  1],
       [ 4,  5],
       [ 8,  9],
       [12, 13]])'''
a[:, :: 2] # 所有行 列数是2的倍数的元素
array([[ 0,  2],
       [ 4,  6],
       [ 8, 10],
       [12, 14]])

当提供的索引少于轴的数量时，缺失的索引被认为是完整的切片

a[1] # [ 4  5  6  7] 等价于 a[0,:]

numpy中数组切片是原始数组的视图，数据不会被复制，视图上任何数据的修改都会反映到原数组上

a = np.arange(6).reshape(2,3)
a[1, -1] = 999
'''array([[  0,   1,   2],
       [  3,   4, 999]])'''

5.3 花式索引和索引技巧

NumPy提供比常规Python序列更多的索引功能。除了通过整数和切片进行索引之外，正如我们之前看到的，数组可以由整数数组和布尔数组索引。 和切片不一样，数组索引它总是将数据复制到新数组中，改变不会反映到原数组中

使用索引数组进行索引

a = np.arange(12).reshape(3,4)
'''[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]'''
b = a[([0,2], [1,2])]  # 找第一、三行同时又是第二、三列，即索引位置（0，1），（2，2）
# 1, 10
b[0] = 1000
display(b)
a

使用布尔数组进行索引

当我们使用（整数）索引数组索引数组时，我们提供了要选择的索引列表。使用布尔索引，方法是不同的; 我们明确地选择我们想要的数组中的哪些项目以及我们不需要的项目。

人们可以想到的最自然的布尔索引方法是使用与原始数组具有 相同形状的 布尔数组：

a = np.arange(12).reshape(3,4)
b = a > 4
print(b)     # b is a boolean with a's shape
a[b]         # 1d array with the selected elements

通常用于数据筛选和数据处理，挺好用的

为什么变与不变？

总之花式索引和普通索引就在于有没有自己的数据，有的话则是花式索引，它不会改变原数组，否则会一变具变。

那为什么会这样呢？相信之前看过id这块内容应该能了解到一点，这与数据结构的存储有关系，具体的数组元素内存分配为不太清楚，但是原理肯定是想通的，给大家看个例子

a = np.arange(12).reshape(3,4)
c = a[:2]
print(id(c[0]), id(a[:3]))
id(c[1]), id(a[:1])

数组的元素所在的内存地址相同，改变一个其他当然也会变了。

6 拷贝与视图

当计算和操作数组时，有时会将数据复制到新数组中，有时则不会。这通常是初学者容易混淆的。有三种情况：

6.1 完全不复制

简单的赋值给变量是不会拥有它自己的数据的，这还是与数据存储结构有关。上案例

a = np.arange(3)
b = a
print(id(b), id(a))
b[0] = 99999
print(id(b),id(a))
a, b

6.2 视图或浅拷贝

不同的数组对象可以共享相同的数据。 view 方法创建一个查看相同数据的新数组对象

a = np.arange(3)
c = a.view()
print('a的id %s  c的id %s' % (id(b), id(c)))
print('数据id', id(c[:]), id(a[:]))
# a的id 140698609490608  c的id 140698603890032
# 数据id 140698602752304 140698602752304

虽然变量id不一样，但数据源的内存地址相同，修改数据时在内存块上修改。索引视图的修改也会影响的原数组

c[1] = 999
# array([  0, 999,   2])

同理浅拷贝也是一样的。切片数组会返回一个视图

6.3 深拷贝

定义：一个变量对另外一个变量的值 拷贝。

注：拷贝的是目标变量的值，是真实的拷贝，新的变量产生了新的内存地址。

深拷贝copy()方法会生产完整的数据和数组副本，就会他有自己的数据，不共用原数组数据，只不过内容相同。

a = np.arange(3)
b = a.copy()
print(b.base is a, b is a, b == a)
# False False [ True  True  True]
b[0] = 111
a #[0, 1, 2]

6.4 深拷贝的用武之地

有时，如果不再需要原始数组，则应在切片后调用 copy。例如，假设a是一个巨大的中间结果，最终结果b只包含a的一小部分，那么在用切片构造b时应该做一个深拷贝， 减少数据量 。

7 线性代数

7.1 单位矩阵

np.eye(3)  # 3x3的单位阵
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])
'''

7.2 矩阵相乘

a = np.arange(6).reshape(2,3)
b = np.arange(9).reshape(3,3)
print(a @ b) # 等价于 a.dot(b), np.dot(a, b)
[[15 18 21]
 [42 54 66]]
输出结果

矩阵转置

a.T
a.transpose()

7.3 矩阵求逆，特征值，特征向量，秩

矩阵的特征值之和等于矩阵的行列式

矩阵的特征值之积等于矩阵的迹

from numpy.linalg import inv,det,eig
A = np.array([[-1,1,0], [-4,3,0], [1,0,2]])
print('逆矩阵\n', inv(A)) 
print('\n行列式', det(A))
print('\n矩阵的秩:', np.linalg.matrix_rank(A))
print('\n主对角线的和（迹）:', np.trace(A))
print('\n特征值:', eig(A)[0])
print('\n特征向量:\n', eig(A)[1])

8 数组拼接

8.1 ''自动"改变数组

要更改数组的尺寸，您可以省略其中一个尺寸（写成-1即可）能避免自己口算错误，然后自动推导出尺寸：

A = np.arange(12).reshape(4,3)
print(A.reshape(2, -1))
A.reshape(-1, 6)

8.2 np.vstack() 纵向拼接数据

v表示竖直，英文单词vertical的首字母，比如要把多个ndarray竖直拼成一个更大的数组，就可以用它。

要求：列数相同

a = np.random.randint(1,100,12).reshape(-1,3)
print(np.vstack([A,a]))

输出结果如下：

[[ 0  1  2]
 [ 3  4  5]
 [ 6  7  8]
 [ 9 10 11]
 [44 59 56]
 [26 51 85]
 [57 50 13]
 [19 82  2]]

8.3 np.hstack() 纵向拼接数据

h表示水平，英文单词horizon的首字母，水平方向连接数组，把数组变的 "更宽了"。

要求：行数相同

print(np.hstack([A,a.reshape(4,-1)]))

输出结果如下：

[[ 0  1  2 44 59 56]
 [ 3  4  5 26 51 85]
 [ 6  7  8 57 50 13]
 [ 9 10 11 19 82  2]]

8.4 np.concatenate((a1, a2, ...), axis=0)

(a1, a2) 要拼接的数组
axis 拼接的方向，默认为0，即沿着0轴拼接(跨行操作)

a = np.arange(6).reshape(2,3)
b = np.arange(11,17).reshape(2,3)
print(np.concatenate([a, b]))
print('\n', np.concatenate([a, b], axis=1))
[[ 0  1  2]
 [ 3  4  5]
 [11 12 13]
 [14 15 16]]
 [[ 0  1  2 11 12 13]
 [ 3  4  5 14 15 16]]

9 数据处理常用函数

abs、sqrt、square、exp、log、sin、cos、tan，maxinmum、minimum、all、any、inner、clip、 round、trace、ceil、floormin、max、mean、median、sum、std、var、cumsum、cumprod、argmin、argmax、 argwhere、cov、corrcoef、sort...

实在是太多了，不一一举例了(有需求可以自己查阅），下面介绍几个用的较多的，以及加深轴（axis）的理解

np.maxinmum() 需要两个或以上的数组，对应位置一一比较，找出更大的那个元素

np.random.seed(123)
a = np.random.randint(10,20,6).reshape(2,3)
b = np.arange(11,17).reshape(2,3)
print(a, '\n\n', b)
# 后续都用这个变量做例子
[[12 12 16]
 [11 13 19]] 
 [[11 12 13]
 [14 15 16]]
np.maximum(a, b)
array([[12, 12, 16],
       [14, 15, 19]])
"""

np.max(a, axis=None)

axis = 0, 轴为0时跨行比较

axis = 1, 轴为1时跨列比较

print('不指定轴方向: ', np.max(a)) # 不指定轴方向则全局比较
print('\n指定轴方向为0: ', np.max(a, axis=0)) 
print('\n指定轴方向为1: ', np.max(a, axis=1)) 
不指定轴方向:  19
指定轴方向为0:  [12 13 19]
指定轴方向为1:  [16 19]
"""

这就是上面提到的轴方向，其他的sum, mean等等，只要axis这个参数，就会涉及到。要小心哦

np.where(condition, [x, y]) 三元运算

如果满足条件，则x，否则y

np.where(a < 15, a, 10*a)
array([[ 12,  12, 160],
       [ 11,  13, 190]])
"""

any()、all() 条件判断
any() 至少有一个为True就会返回True
all() 全为True才会返回True

a = np.array([True, False, True])
print(a.any(), a.all())
# True  False

np.cumsum(arr) 累加计算

a = np.array([1, 2, 3])
np.cumsum(a)
# array([1, 3, 6])

np.cumprod(arr) 累乘计算

a = np.array([1, 2, 4])
np.cumprod(a)
# array([1, 2, 8])

np.sort(arr, axis=-1) 二维情况下默认是根据每一行排序的
axis=0 跨行升序排序，比较每一列，小的放上面
axis=1 跨列升序排序，比较每一行，小的放左边

np.random.seed(12)
a = np.random.randint(1,100,6).reshape(2,3)
print(a)
[[76 28  7]
 [ 3  4 68]]
print(np.sort(a, axis=0))
[[ 3  4  7]
 [76 28 68]]
print(np.sort(a, axis=1))