布谷鸟哈希(Cuckoo hash)
最近看了下布谷鸟哈希(Cuckoo hash),cuckoo hash是2002年提出来的老算法了,它可以应用在数据库的哈希表中, 查找(lookup)非常快,而且可以向量化查找 ,这到底一种什么样的算法呢?一起来看看
布谷鸟的行为
首先要理解布谷鸟的行为,这也是算法的核心,可以观看一下动物世界布谷鸟的视频, 布谷鸟不建巢却能让别人帮它孵蛋,出生后又将其他三个兄弟毁掉_哔哩哔哩_bilibili ,这个三分钟的视频说了两个关键点:
- 布谷鸟妈妈从不筑巢,它将自己的鸟蛋生在其他鸟类的巢穴里,要别的鸟给它孵蛋
- 新出生的布谷鸟会本能地将巢穴里的其他蛋踢开(kick out ) , 推出鸟巢 ,以确保自己在鸟巢里可以独享宠爱
可用说“有其母必有其子”了,两个都很贱hh
一个哈希桶的版本
布谷鸟哈希有几种变种,先介绍 一个哈希桶和两个哈希函数 的版本
insert逻辑 :
- 若值x已存在哈希表中,则直接返回
- 若insert后哈希表空间会不够,则先进行扩容,再rehash,再继续3、4、5
- 用哈希函数h1(x)计算出下标i1,当bucket[i1]为空时,说明鸟巢可用,插入x
- 若bucket[i1]非空,用新值x将bucket[i1]上的老值x'踢开(kick out), 对应小布谷鸟将老蛋踢出巢穴,老蛋当然也不能坐以待毙,继续kick out别的蛋 ,老值x'的下一个位置用哈希函数h2(x)寻找
- 重复2,直到达到最大循环次数MaxLoop(插入失败);或者所有被踢开的值都找到新位置(插入完成)
lookup逻辑 :查找逻辑非常简单,去可能的两个巢穴里寻找,即去下标h1(x)和h2(x)寻找,若没有匹配上,则不存在(从这里可以发现查找是非常快的,且时间复杂度稳定是O(1))
insert伪代码:
insert(x)
if lookup(x) then return // 待插入值已存在哈希表中 返回
if (nums+1 >= load_factor * cap) { rehash();insert(x) } // 空间不够,扩容
loop MaxLoop times
if bucket[h1(x)] = null then { bucket[h1(x)] = x; return }
swap(bucket[h1(x)],x) // kick out old value
if bucket[h2(x)] = null then { bucket[h2(x)] = x; return }
swap(bucket[h1(x)],x) // kick out old value
end loop
// 插入失败
endlookup伪代码:
function lookup(x)
return bucket[h1(x)] == x or bucket[h2(x)] == x
举个例子,插入129、875、312和234到哈希表中,哈希函数h1(x)是x%5,发生哈希冲突时使用哈希函数h2(x)=(x/10)%5
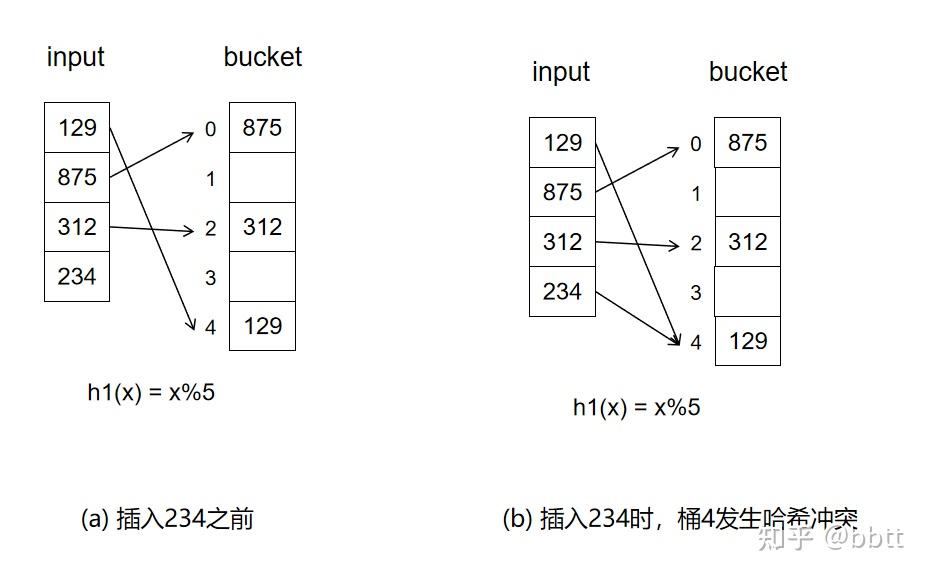
在插入234之前,没有哈希冲突,下标都用h1(x)=x%5计算出,如上图(a)
插入234时,234和129在桶4发生哈希冲突,上图(b)
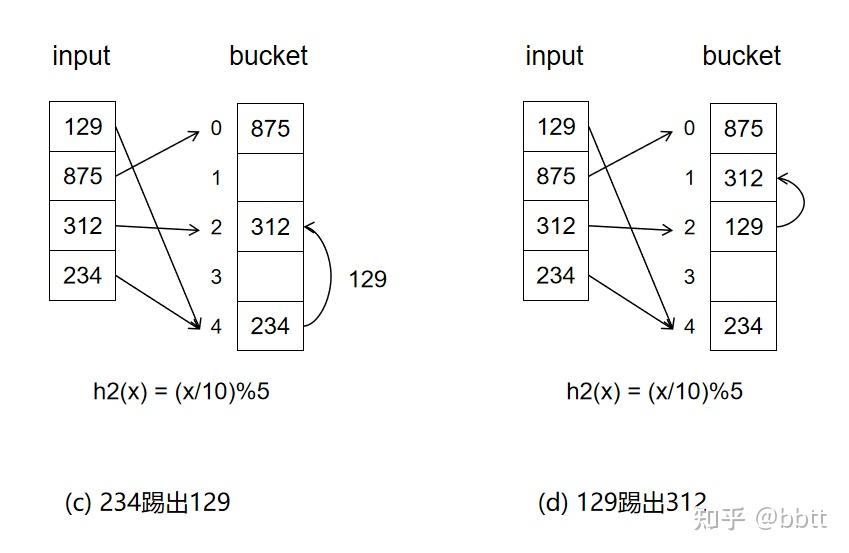
新元素234踢出老元素129,老元素129下一个可能的巢穴用h2(x)=(x/10)%5计算得出,是2,上图(c)
下标2(桶2)继续发生哈希冲突,新来者129踢出老元素312,312下一个可能的巢穴是1,是空,可以插入,上图(d)
所有元素都插入,insert完成.
两个桶的版本
能看懂这张图也就看懂两个桶的版本了
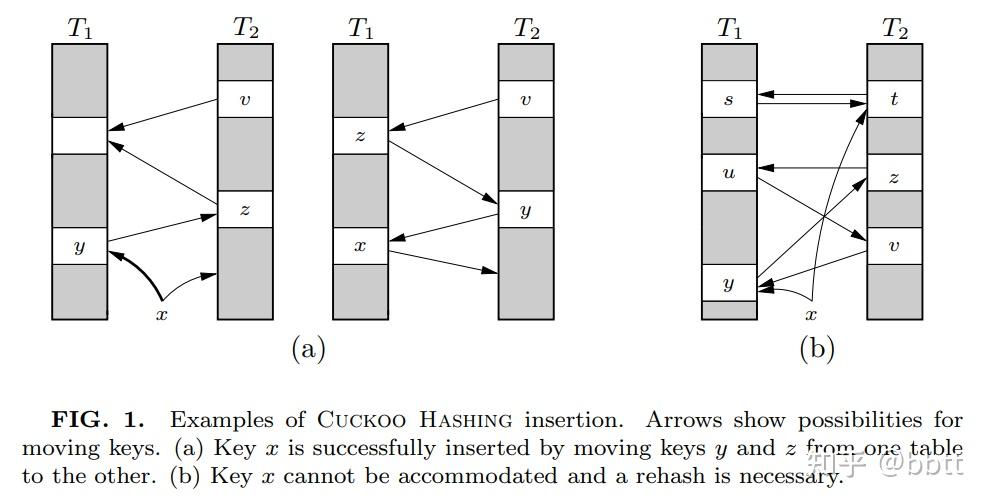
图(a)解析:想插入元素x,用哈希函数h1(x)计算出下标i1,发现巢穴中i1已经存在元素y,于是用x踢开y;y用哈希函数h2(x)计算出下一个下标,发现存在元素z,于是用y踢开z;z用哈希函数h1(x)计算出下一个下标,填充进去,算法结束。
注意:在T1的元素发生哈希冲突时,用h2(x)去计算下一个下标、在T2的元素发生哈希冲突时,用h1(x)去计算下一个下标。
图(b)解析:想插入元素x,x踢出y,y踢出z,z踢出u,u踢出v,v踢出x....形成死循环,达到最大插入限制后,在T1插入失败;转而在T2插入,x踢出t,t踢出s,s踢出x...形成死循环,达到最大插入限制后,在T2插入失败,算法结束。
insert伪代码:
insert(x)
if lookup(x) then return
loop MaxLoop times
if T1[h1(x)] = ⊥ then { T1[h1(x)] ← x; return }
x ↔ T1[h1(x)]
if T2[h2(x)] = ⊥ then { T2[h2(x)] ← x; return }
x ↔ T2[h2(x)]
end loop
rehash(); insert(x)
注:← 代表赋值;↔ 代表swap交换;⊥ 代表空值
lookup伪代码:
function lookup(x)
return T1[h1(x)] = x ∨ T2[h2(x)] = x
end注:∨ 代表或
布谷鸟哈希在查找时如何向量化?
每个鸟蛋有两个可能的巢穴,要么在h1(x),要么在h2(x),或者都不在,但引入分支的话会让代码不能向量化执行, 工程上可以采用mask的技巧消除分支
看代码:
...
// check which one matches
i1 = h1(input[i]); // two possible idx
i2 = h2(input[i]);
