工程热动力学基础（二）

Chapter 2 Energy and the First Law of Thermodynamics

2.1 Reviewing Mechanical Concepts of Energy

2.1.1 Work and Kinetic Energy

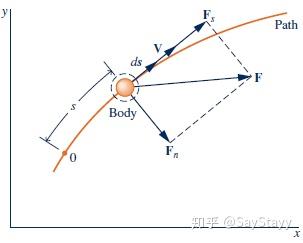
• Kinetic energy: \frac{1}{2}m{V^2} , KE.

The work of the resultant force on the body equals the change in its kinetic energy.
Kinetic energy is associated with the body as a whole, it is an extensive property. 

2.1.2 Potential Energy

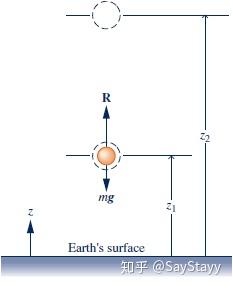
\begin{array}{l} \frac{1}{2}m(V_2^2 - V_1^2) = \int_{{z_1}}^{{z_2}} {Rdz} - \int_{{z_1}}^{{z_2}} {mgdz} \\ \int_{{z_1}}^{{z_2}} {mgdz} = mg({z_2} - {z_1})\\ \frac{1}{2}m(V_2^2 - V_1^2) + mg({z_2} - {z_1}) = \int_{{z_1}}^{{z_2}} {Rdz} \end{array}

• Gravitational potential energy, mgz , PE.
• Potential energy is an extensive property of the body

2.1.3 Units for Energy

• N·m=J, kJ
• ft·lbf
• Btu

2.1.4 Conservation of Energy in Mechanics

\begin{array}{l} \frac{1}{2}m(V_2^2 - V_1^2) + mg({z_2} - {z_1}) = 0\\ \frac{1}{2}mV_2^2 + mg{z_2} = \frac{1}{2}mV_1^2 + mg{z_1} \end{array}
2.1.5 Closing Comment
2.2 Broadening Our Understanding of Work

• Thermodynamic definition of work : Work is done by a system on its surroundings if the sole effect on everything external to the system could have been the raising of a weight.
• The raising of a weight is a force acting through a distance.

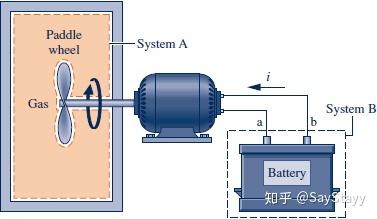
• Work is a means for transferring energy. Energy is transferred and stored when work is done.

2.2.1 Sign Convention and Notation

• The value of W depends on the details of the interactions taking place between the system and surroundings during a process and not just the initial and final states of the system.
• Work is not a property of the system or the surroundings.
• Exact differentials are written using the symbol d; The symbol δ is used to identified inexact differentials.

2.2.2 Power

• Power: the rate of energy transfer by work.
• J/s
• ft·lbf/s
• Btu/h
• hp

2.2.3 Modeling Expansion or Compression Work

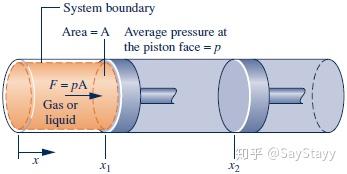
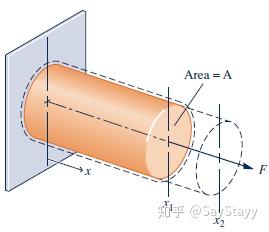
\delta W = pAdx = pdV W = \int_{{V_1}}^{{V_2}} {pdV}
2.2.4 Expansion or Compression Work in Actual Processes
2.2.5 Expansion or Compression Work in Quasi-equilibrium Processes

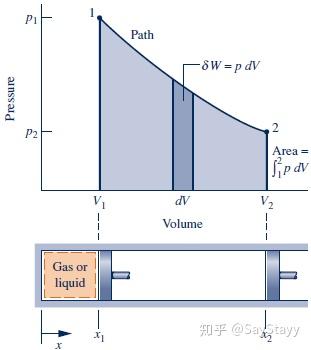
• work is not a property; The value of work depends on the nature of the process between the end states.
• Polytropic process: A quasi-equilibrium process described by p{V^n} = {\mathop{\rm constant}\nolimits} , p{v^n} = {\mathop{\rm constant}\nolimits} , where n is a constant.

2.2.6 Further Examples of Work

• Extension of a Solid Bar

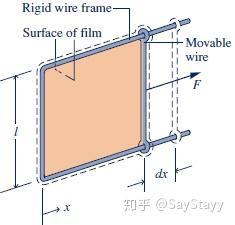
• Stretching of a Liquid Film

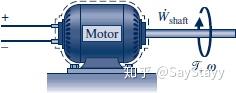
• Power Transmitted by a Shaft

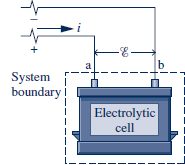
• Electric Power

• Work Due to Polarization or Magnetization

2.2.7 Further Examples of Work in Quasi-equilibrium Processes

• ideal situation: external forces acting on the system are varied so slightly that the resulting imbalance is infinitesimal.
• The extension of a solid bar and the stretching of a liquid surface can be viewed as a quasi-equilibrium example.
• an electrolytic cell's being charged or discharged.
• a dielectric material residing in a uniform electric field.

2.2.8 Generalized Forces and Displacements
\delta W = pdV - \sigma d(Ax) - \tau dA - \xi dZ - E \cdot d(VP) - {\mu _0}H \cdot d(VM) + \cdots

• The last three dots represent other products of an intensive property and the differential of a related extensive property that account for work.

2.3 Broadening Our Understanding of Energy

• Consider the total energy of a system.
• Work can be done on systems to increase the energy stored within those systems.
• Three macroscopic methods contributing to the change in total energy: kinetic energy, gravitational potential energy, and internal energy .

Like kinetic energy and gravitational potential energy, 
internal energy is an extensive property of the system,
as is the total energy

• Internal energy: U
• The change in the total energy of a system:

\Delta E = \Delta U + \Delta KE + \Delta PE

• Internal energy is a macroscopic form of energy.
• Microscopic interpretation of internal energy:

the translational kinetic energy of the molecules; 
rotation of the molecules relative to their centers of mass;
the kinetic energy associated with vibrational motions within the molecules.
chemical bonds between the atoms.

2.4 Energy Transfer by Heat

• Interact with surroundings: work & heat
• energy transfer by heat

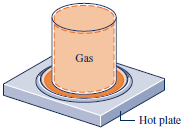
2.4.1 Sign Convention, Notation, and Heat Transfer Rate

• Q : Heat transfer into a system is taken to be positive, and heat transfer from a system is taken as negative.
• Heat is not a property.

The value of a heat transfer depends on the details of a process 
and not just the end states.

Q = \int_1^2 {\delta Q}

• Rate of heat transfer:

Q = \int_{{t_1}}^{{t_2}} {\mathop Q\limits^. dt}

• Heat flux: the heat transfer rate per unit of system surface area. Unit: kW/{m^2} or Btu/h \cdot f{t^2} .

\mathop Q\limits^. = \int\limits_A {\mathop q\limits^. } dA

• Adiabatic means without heat transfer.

2.4.2 Heat Transfer Modes

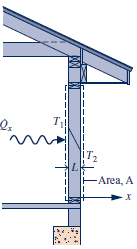
• Conduction
• Fourier's law: the rate of heat transfer across any plane normal to the x direction, \mathop {{Q_x}}\limits^. , is proportional to the wall area, A, and the temperature gradient in the x direction, dT/dx :

\mathop {{Q_x}}\limits^. = - \kappa A\frac{{dT}}{{dx}}

• proportionality constant \kappa is thermal conductivity .

• Radiation

a result of changes in the electronic configurations of the atoms or molecules
transported by electromagnetic waves (or photons). 
requires no intervening medium

• Stefan–Boltzmann law: The rate at which energy is emitted, \mathop {{Q_e}}\limits^. , from a surface of area A is quantified by:

\mathop {{Q_e}}\limits^. = \varepsilon \sigma AT_b^4

• T_b is the absolute temperature of the surface, The emissivity \varepsilon is a property of the surface that indicates how effectively the surface radiates. \sigma is the Stefan–Boltzmann constant :

\sigma = 5.67 \times {10^{ - 8}}W/{m^2} \cdot {K^4} = 0.1714 \times {10^{ - 8}}Btu/h \cdot f{t^2} \cdot {}^ \circ {R^4}

• Net rate of energy transfer:

\mathop {{Q_e}}\limits^. = \varepsilon \sigma A\left[ {T_b^4 - T_s^4} \right]

• Convection : Energy transfer between solid surface and gas(liquid).
• Newton's law of cooling: the rate of energy transfer from the surface to the air can be quantified by
  \mathop {{Q_e}}\limits^. = hA\left( {{T_b} - {T_f}} \right)
• A is the surface area and the proportionality factor h is the heat transfer coefficient.

The heat transfer coefficient is not a thermodynamic property.

2.4.3 Closing Comments

The term heat does not refer to what is being transferred
or to what is stored within systems. 
Energy is transferred and stored when heat transfer occurs.

2.5 Energy Accounting: Energy Balance for Closed Systems

• First law of thermodynamics: energy is conserved.
• Summarizing Energy Concepts:

• Energy balance:

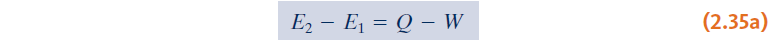
Introducing：

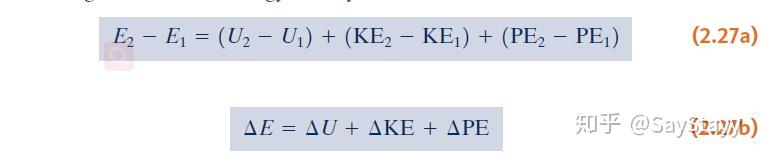
we can get:

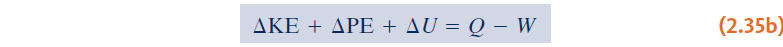
A minus sign appears before W because energy transfer by work from the system
to the surroundings is taken to be positive.
A plus sign appears before Q because it is regarded to be positive 
when the heat transfer of energy is into the system from the surroundings.

2.5.1 Important Aspects of the Energy Balance

• Differential form of energy balance:

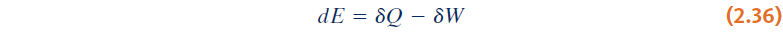
• Time rate form of the energy balance:

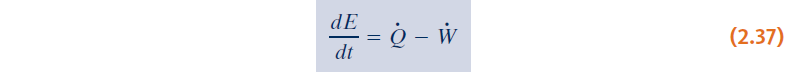
• It can be stated as:

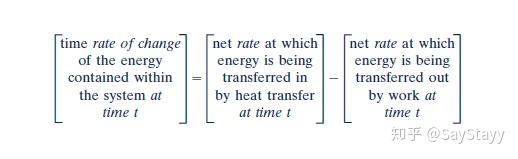
Since the time rate of change of energy is:

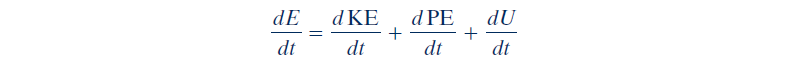
Time rate form of the energy balance can also be:

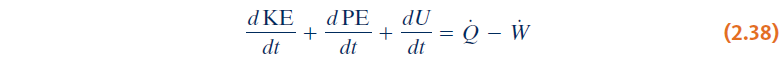
• Closing Comments

2.5.2 Using the Energy Balance: Processes of Closed Systems

• Cooling a Gas in a Piston–Cylinder

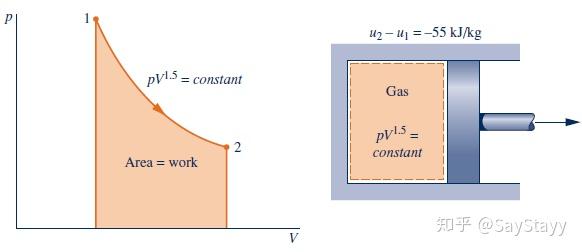
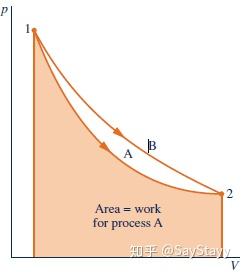
The given relationship between pressure and volume allows the process to be
represented by the path shown on the accompanying diagram. The area under
the curve represents the work. Since they are not properties, the values of the
work and heat transfer depend on the details of the process and cannot be
determined from the end states only.
The minus sign for the value of Q means that a net amount of energy has
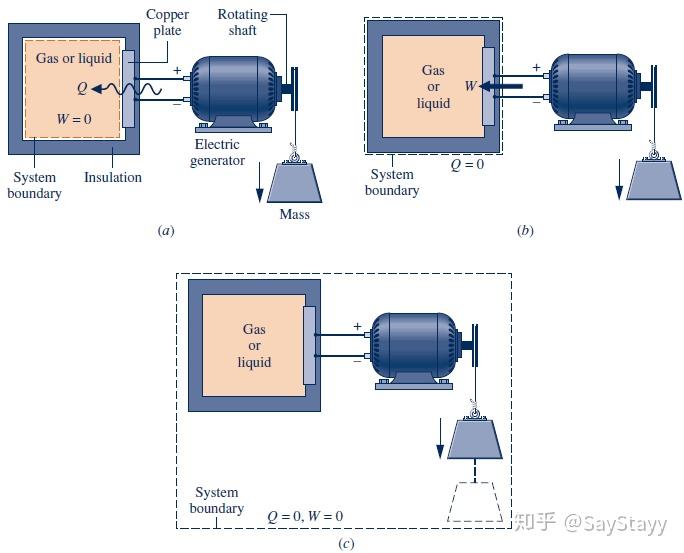
been transferred from the system to its surroundings by heat transfer.

• Considering Alternative Systems

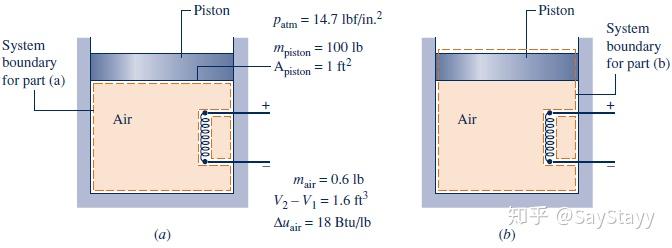
Although the value of Q is the same for each system, observe that the values
for W differ. Also, observe that the energy changes differ, depending on
whether the air alone or the air and the piston is the system.

2.5.3 Using the Energy Rate Balance: Steady-State Operation

A system is at steady state if none of its properties change with time.

• Evaluating Energy Transfer Rates of a Gearbox at Steady State

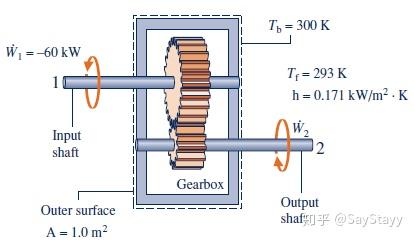
Properties of a system at steady state do not change with time. Energy E is
a property, but heat transfer and work are not properties.

• Determining Surface Temperature of a Silicon Chip at Steady State

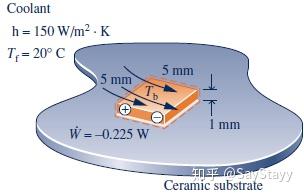
2.5.4 Using the Energy Rate Balance: Transient Operation

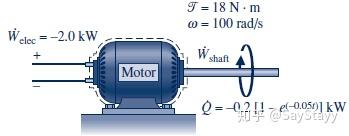
2.6 Energy Analysis of Cycles

Thermodynamic cycle : a sequence of processes that begins and ends at the same state.

steam circulating through an electrical power plant executes a cycle.

2.6.1 Cycle Energy Balance

• The energy balance for any system undergoing a thermodynamic cycle:

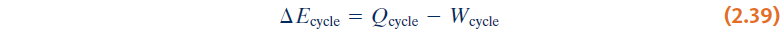
Since the system is returned to its initial state after the cycle:

• Power cycles & refrigeration and heat pump cycles

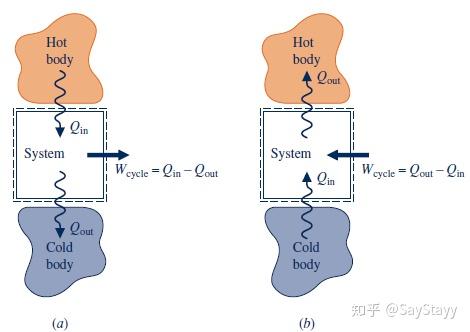
2.6.2 Power Cycles

• Power cycle

Deliver a net work transfer of energy to their surroundings during each cycle

where Q_{in} represents the heat transfer of energy into the system from the hot body, and Q_{out} represents heat transfer out of the system to the cold body.

• Thermal efficiency

The extent of the energy conversion from heat to work

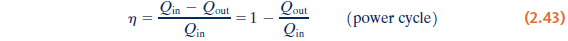
2.6.3 Refrigeration and Heat Pump Cycles

• Refrigeration and heat pump cycles

Q_{in} is the energy transferred by heat into the system undergoing the cycle from the cold body, and Q_{out} is the energy discharged by heat transfer from the system to the hot body.

• Refrigeration Cycles

The objective of a refrigeration cycle is to cool a refrigerated space or  to maintain the 
temperature within a dwelling or other building below that of the surroundings.

• Coefficient of performance

the ratio of the amount of energy received by the system undergoing the cycle 
from the cold body to the net work into the system to accomplish this effect.

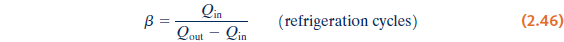
• Heat Pump Cycles

The objective of a heat pump is to maintain the temperature within a dwelling or 
other building above that of the surroundings or to provide heating for certain 
industrial processes that occur at elevated temperatures.

• Coefficient of performance

the ratio of the amount of energy discharged from the system undergoing the cycle