【Python进阶】克里金插值法的实现过程
一、克里金插值法介绍
克里金算法提供的半变异函数模型有高斯、线形、球形、阻尼正弦和指数模型等,在对气象要素场插值时球形模拟比较好。既考虑了储层参数的随机性,有考虑了储层参数的相关性,在满足插值方差最小的条件下,给出最佳线性无偏插值,同时还给出了插值方差。
与传统的插值方法(如最小二乘法、三角剖分法、距离加权平均法)相比,克里金法的优势:
1、在数据网格化的过程中考虑了描述对象的空间相关性质,使插值结果更科学、更接近于实际情况;
2、能给出插值的误差(克里金方差),使插值的可靠程度一目了然
插值方差:就是指实际参数值 zv 与估计值 zv* 两者偏差平方的数学期望:
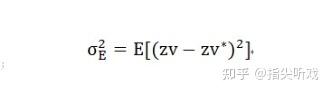
而插值点的 zv*,通过N个离散点获得;
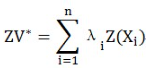
其中λ与N个离散点指的是加权系数; *变差函数的理论模型*
变差函数与随机变量的距离h存在一定的关系,这种关系可以用理论模型表示。常用的变差函数理论模型包括球状模型、高斯模型与指数模型(还包括:具基台值线性模型、幂函数模型、无基台值线性模型);
1、 球状模型公式:
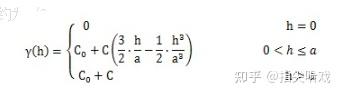
2、 高斯模型公式:
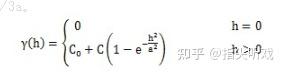
3、 指数模型公式:
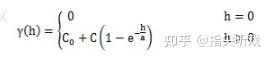
4、 具基台值线性模型:
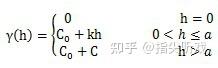
5、 幂函数模型:
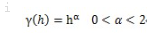
式中: 为幂指数;不存在基台值。两边取对数得ln(γ(h))=αlnh,线性化为γ(hi)=b1X1,i
6、 无基台值线性模型:
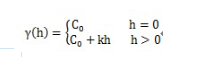
式中:k为直线斜率;不存在基台值和变程,当h>0时, γ(hi)=b0+b1X1,i
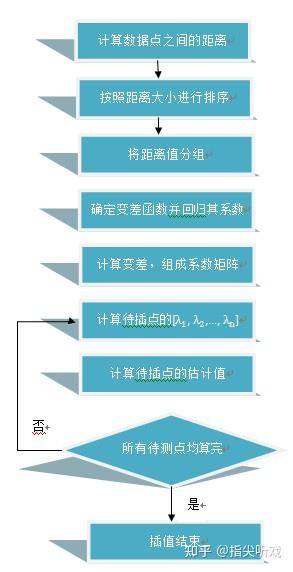
普通克里格方法的基本步骤如下 :

二、算法实现
代码实现:
from gma.algorithm.spmis.interpolate import *
class Kriging(IPolate):
'''克里金法插值'''
# 继承 gma 的标准插值类 IPolate。本处不再做详细说明。
def __init__(self, Points, Values, Boundary = None, Resolution = None,
InProjection = 'WGS84',
VariogramModel = 'Linear',
VariogramParameters = None,
**kwargs):
IPolate.__init__(self, Points, Values, Boundary, Resolution, InProjection)
self.eps = eps
# 初始化半变异函数及参数
self.VariogramModel, self.VParametersList = GetVariogramParameters(VariogramModel, VariogramParameters)
self.VariogramFUN = getattr(variogram, self.VariogramModel)
if self.VParametersList is None:
self.VParametersList = self._INITVariogramModel(**kwargs)
# 调整输入数据
if self.GType == 'PROJCS':
self.Center = (self.Points.min(axis = 0) + self.Points.max(axis = 0)) * 0.5
self.AnisotropyScaling = AnisotropyScaling
self.AnisotropyAngle = AnisotropyAngle
self.DistanceMethod = cdist
else:
# 方便后期优化
self.Center = np.array([0,0])
self.AnisotropyScaling = 1.0
self.AnisotropyAngle = 0.0
self.DistanceMethod = GreatCircleDistance
self.AdjustPoints = AdjustAnisotropy(self.Points, self.Center,
[self.AnisotropyScaling],
[self.AnisotropyAngle])
self.XYs = AdjustAnisotropy(self.XYs, self.Center,
[self.AnisotropyScaling],
[self.AnisotropyAngle])
def _INITVariogramModel(self, **kwargs):
'''初始化参数'''
if 'NLags' in kwargs:
NLags = kwargs['NLags']
initialize.ValueType(NLags, 'pint')
else:
NLags = 6
if 'Weight' in kwargs:
Weight = ToNumericArray(kwargs['Weight']).flatten().astype(bool)[0]
else:
Weight = False
Lags, SEMI = INITVariogramModel(self.Points, self.Values, NLags, self.GType)
# 为求解自动参数准备
if self.VariogramModel == "Linear":
X0 = [np.ptp(SEMI) / np.ptp(Lags), np.min(SEMI)]
BNDS = ([0.0, 0.0], [np.inf, np.max(SEMI)])
elif self.VariogramModel == "Power":
X0 = [np.ptp(SEMI) / np.ptp(Lags), 1.1, np.min(SEMI)]
BNDS = ([0.0, 0.001, 0.0], [np.inf, 1.999, np.max(SEMI)])
else:
X0 = [np.ptp(SEMI), 0.25 * np.max(Lags), np.min(SEMI)]
BNDS = ([0.0, 0.0, 0.0], [10.0 * np.max(SEMI), np.max(Lags), np.max(SEMI)])
# 最小二乘法求解默认参数
def _VariogramResiduals(Params, X, Y, Weight):
if Weight:
Weight = 1.0 / (1.0 + np.exp(-2.1972 / (0.1 * np.ptp(X)) * (0.7 * np.ptp(X) + np.min(X) - x))) + 1
else:
Weight = 1
return (self.VariogramFUN(X, *Params) - Y) * Weight
RES = least_squares(_VariogramResiduals, X0, bounds = BNDS, loss = "soft_l1",
args = (Lags, SEMI, Weight))
return RES.x
def _GetKrigingMatrix(self):
"""获取克里金矩阵"""
LDs = self.DistanceMethod(self.AdjustPoints, self.AdjustPoints)
A = -self.VariogramFUN(LDs, *self.VParametersList)
A = np.pad(A, (0, 1), constant_values = 1)
# 填充主对角线
np.fill_diagonal(A, 0.0)
return A
def _UKExec(self, A, LDs, SearchRadius):
"""泛克里金求解"""
Args = LDs.argsort(axis = 1)[:,:SearchRadius]
Values = self.Values[Args.T].T
# A 的逆矩阵
AInv = inv(A)
B = -self.VariogramFUN(LDs, *self.VParametersList)
B[np.abs(LDs) <= self.eps] = 0.0
B = np.pad(B, ((0,0),(0,1)), constant_values = 1)
X = np.dot(B, AInv)
B = B[np.ogrid[:len(B)], Args.T].T
X = X[np.ogrid[:len(X)], Args.T].T
X = X / X.sum(axis = 1, keepdims = True)
UKResults = np.sum(X * Values, axis = 1), np.sum((X * -B), axis = 1)
return UKResults
def _OKExec(self, A, LDs, SearchRadius):
"""普通克里金求解"""
Args = LDs.argsort(axis = 1)[:,:SearchRadius]
LDs = LDs[np.ogrid[:len(LDs)], Args.T].T
B = -self.VariogramFUN(LDs, *self.VParametersList)
B[np.abs(LDs) <= self.eps] = 0.0
B = np.pad(B, ((0,0),(0,1)), constant_values = 1)
OKResults = np.zeros([2, len(LDs)])
for i, b in enumerate(B):
BSelector = Args[i]
ASelector = np.append(BSelector, len(self.AdjustPoints))
a = A[ASelector[:, None], ASelector]
x = solve(a, b)
OKResults[:, i] = x[:SearchRadius].dot(self.Values[BSelector]), -x.dot(b)
return OKResults
def Execute(self, SearchRadius = 12, KMethod = 'Ordinary'):
'''克里金插值'''
initialize.ValueType(SearchRadius, 'pint')
SearchRadius = np.min([SearchRadius, len(self.AdjustPoints)])
A = self._GetKrigingMatrix()
LDs = self.DistanceMethod(self.XYs, self.AdjustPoints)
if KMethod not in ['Universal', 'Ordinary']:
raise ValueError("Undefined Kriging method. Please select 'Universal' or 'Ordinary'!")
elif KMethod == 'Universal':
KResults = self._UKExec(A, LDs, SearchRadius)
else:
KResults = self._OKExec(A, LDs, SearchRadius)
NT = namedtuple('Kriging', ['Data', 'SigmaSQ', 'Transform'])
return NT(KResults[0].reshape(self.YLAT, self.XLON),
KResults[1].reshape(self.YLAT, self.XLON), self.Transform)三、差值应用
示例数据可从: https:// gma.luosgeo.com/ 获取
在 gma 1.0.13.15 之后的版本可以直接引用。这里基于 1.0.13.15之后的版本引用做示例。
import gma
import pandas as pd
Data = pd.read_excel("Interpolate.xlsx")
Points = Data.loc[:, ['经度','纬度']].values
Values = Data.loc[:, ['值']].values
# 普通克里金(球面函数模型)插值
KD = gma.smc.Interpolate.Kriging(Points, Values, Resolution = 0.05,
VariogramModel = 'Spherical',
VariogramParameters = None,
KMethod = 'Ordinary',
InProjection = 'EPSG:4326')
# 泛克里金类似,这里不做示例
