友情提示: 本文将给出求解 多旅行商 问题的模拟退火算法的思路,因此想完全弄懂本文的思想,请先提前观看我在b站发布的模拟退火视频,在这个视频中有单个旅行商问题的讲解:
我们先来简单回顾下上面这个视频中的内容:
(1)旅行商问题(TravelingSalesmanProblem,TSP)是一个经典的组合优化问题。 经典的TSP可以描述为:一个商品推销员要去若干个城市推销商品,该推销员从一个城市出发,需要经过所有城市后,回到出发地。应如何选择行进路线,以使总的行程最短。
(2)由于TSP问题的解是一个闭环,因此在模拟退火中构造初始解和新解时,我们不需要指定起点位置。
(3)产生新解我们给了三种方法,分别是 交换法,移位法和倒置法。
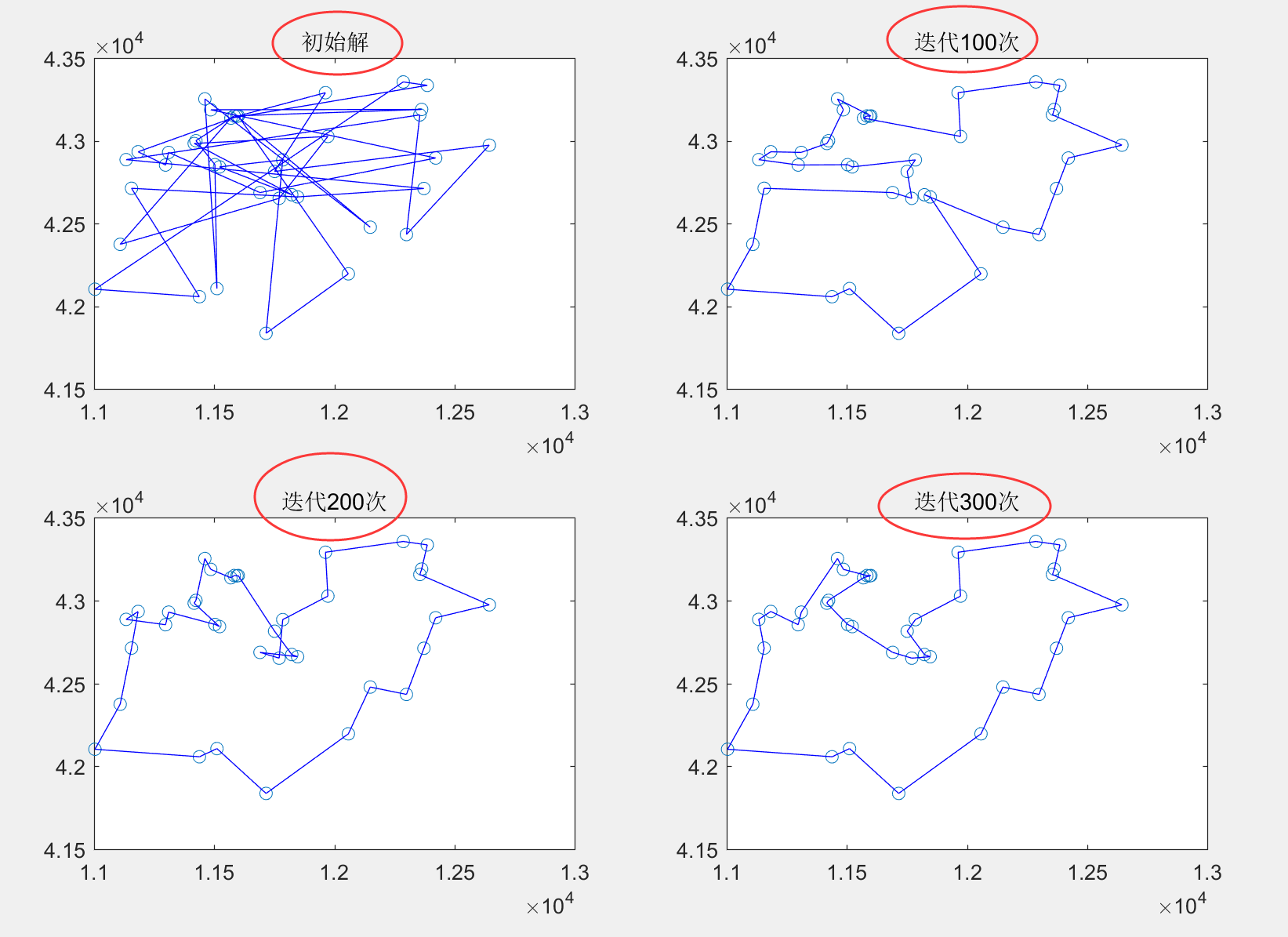
下面这个图就是模拟退火求解单旅行商问题中的四个时刻的状态图,左上是初始解时候对应的图像,可以看出初始解非常的乱;经过100次迭代后,我们得到了右上的图像,可以看出,此时旅行商的路径已经整齐了很多;到迭代300次时,我们得到的解已经非常好了。
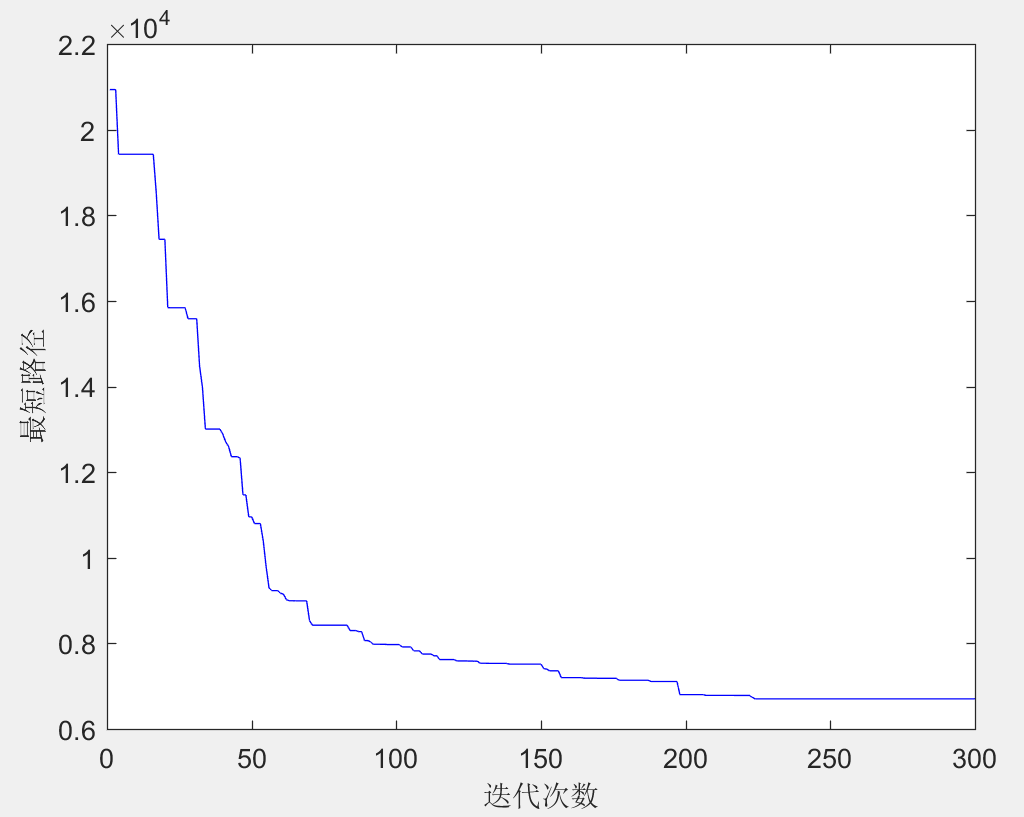
另外,我们也可以画图每次迭代后找到的最优解的图形,如下图所示,随着迭代次数的增加,我们找到的最优解对应的行程越来越短:
下面我们就来正式介绍多旅行商问题 。
首先先给大家指出一个概念,在运筹学中有一个很著名的问题: 车辆路径问题(Vehicle Routing Problem,VRP) ,这个问题有很多种不同的变形,也是运筹学界目前研究的热点问题之一, 今天我们学习的多旅行商问题,大家可以视为VRP问题较为简单的一个例子 ,未来有机会我再给大家讲解几类常见的VRP的求解。下图为MBA智库百科对于车辆路径规划的介绍,大家课后可以自己搜索:
下面我先给出一个 多旅行商问题的定义 ,可能和你在其他地方见到的有所不同,不过都大同小异:
经典的TSP可以描述为: 一个商品推销员要去若干个城市推销商品,该推销员从一个城市出发,需要经过所有城市后,回到出发地。
多旅行商问题MTSP可以描述为: 多个商品推销员要去若干个城市推销商品,这些 推销员最开始都在同一个城市 ,他们可以被分配到不同路径,在经过所有的城市后,大家都回到出发的城市。
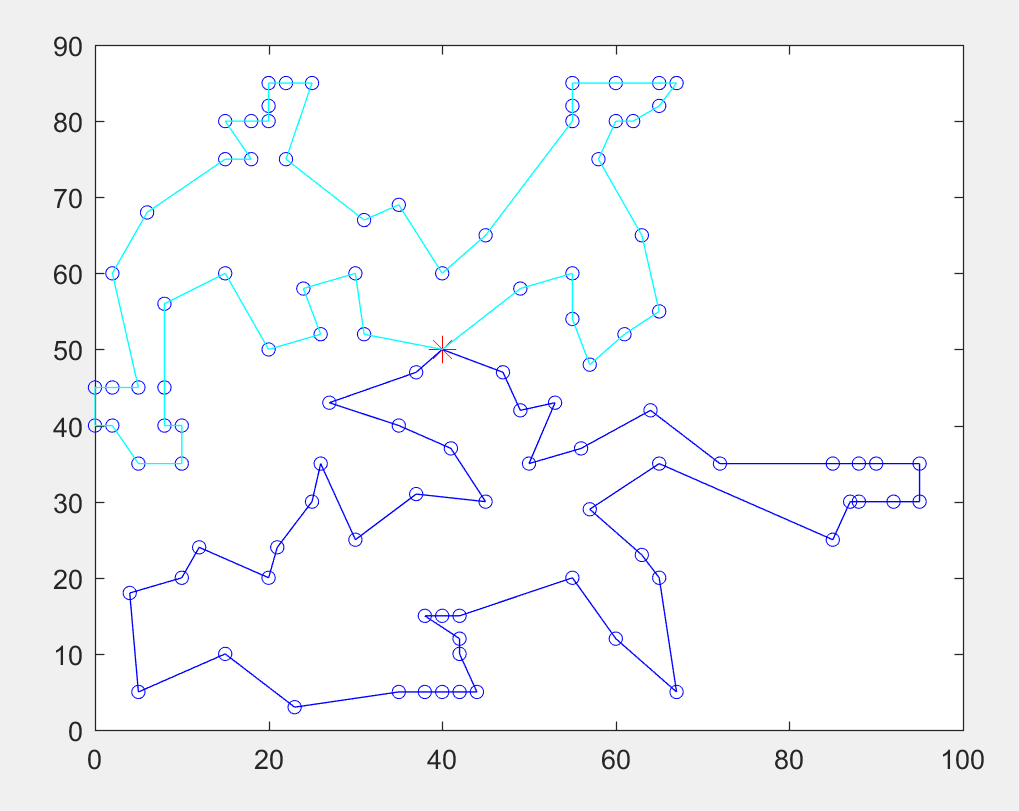
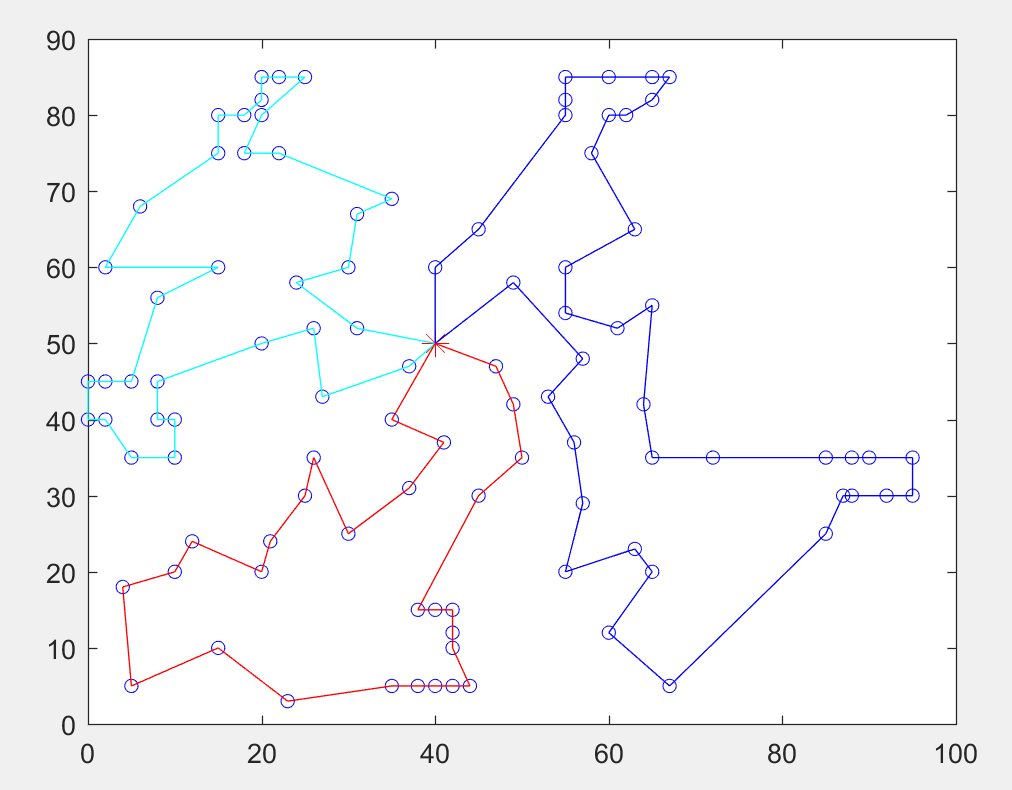
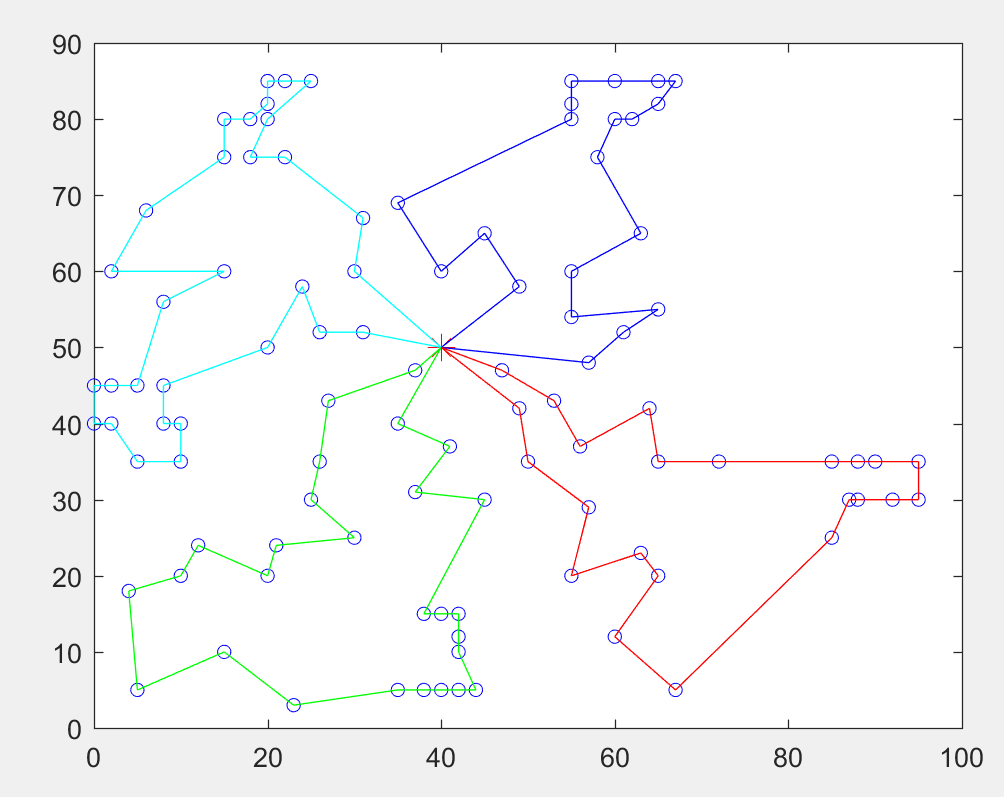
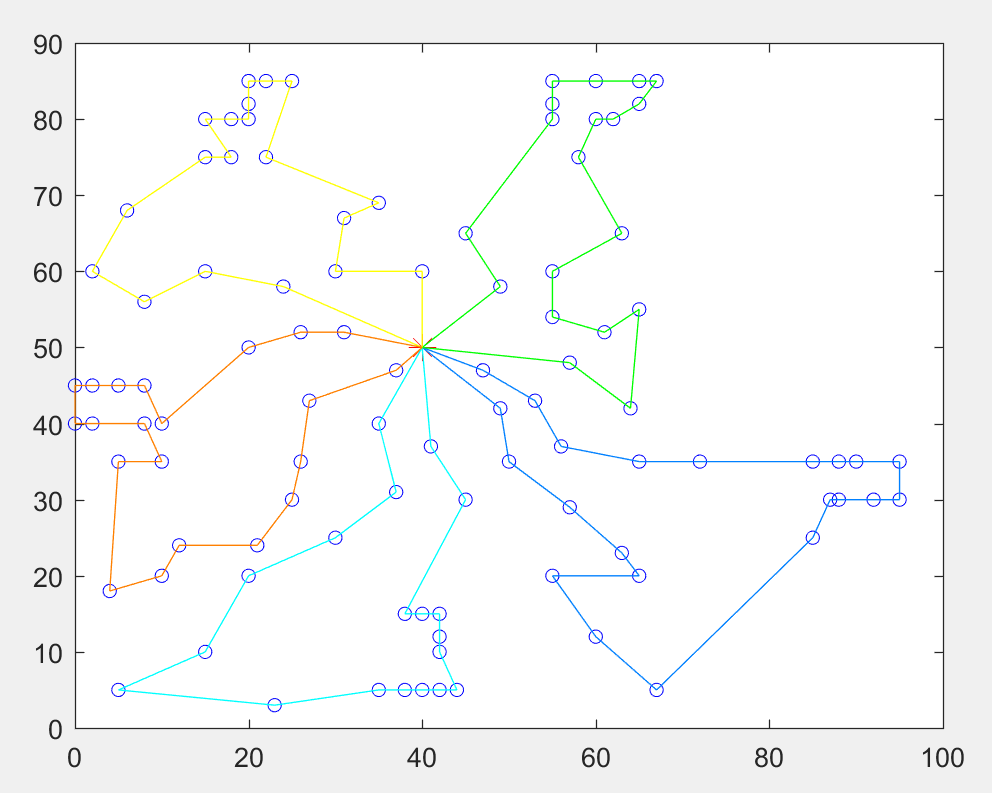
为了让大家直观的感受下MTSP和TSP的差异,这里有几张图片,分别是存在1,2,3,4,5个推销商时候的情况(图中红色的*表示开始的城市)。
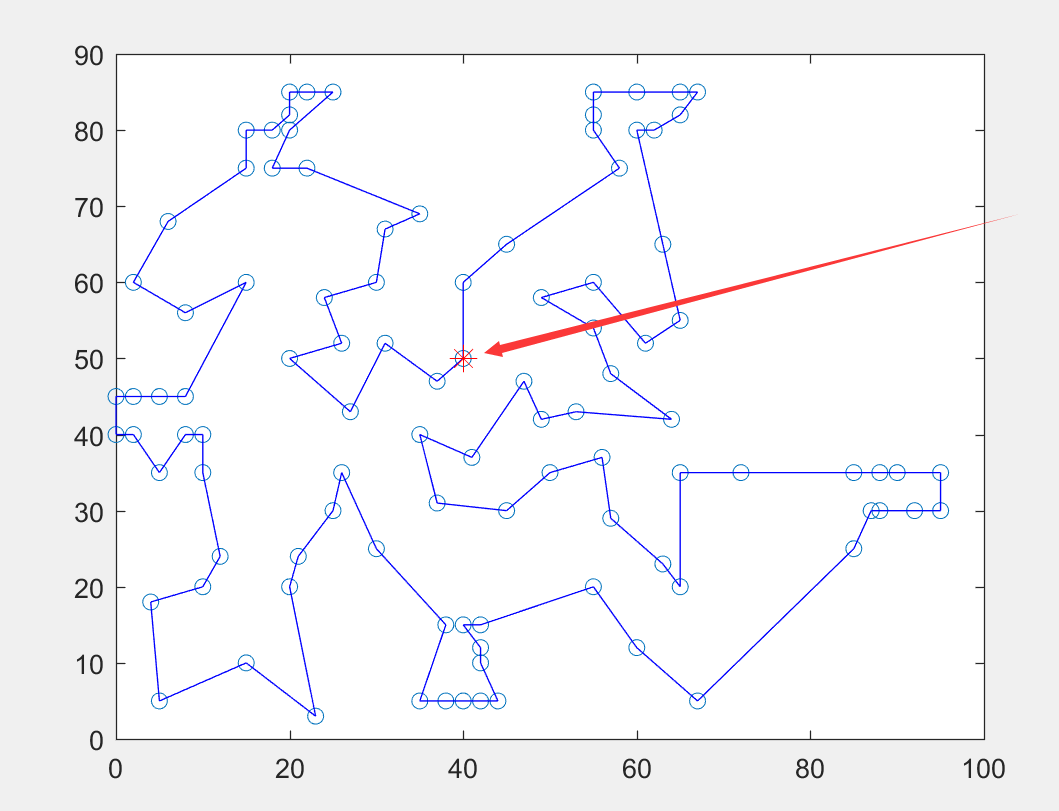
这里一共有101个城市,第一个图就是我们之前学的TSP,可以看出,TSP的解形成的路径构成了一个闭环,因此在TSP问题中初始所在的城市我们不用单独去考虑, TSP中的初始解我们可以用1 至 n的一个随机排序。
例如我们将这101个城市依次编号为1,2,3,…,101,假设初始的城市编号为35,我们得到的最短路径的编号为 3-59-78-…-12-35-91-…-3,这时候我们重新组合下这个编号,将其以35开头和35结尾,即:35-91-…-3-59-78-…-12-35,这时候这个解就是我们想要的解。 (这里看的不懂的请看本文最开始的那个视频,否则你下面的应该也看不懂啦)
在下面的四张图就是我们要介绍的MTSP,大家应该能看出,我们的旅行商都选择了不同的城市,且分别以起始城市围成了一个圈。
接下来就要告诉大家,MTSP中解长什么样子?
如果你看了模拟退火的视频,你就应该知道: 模拟退火里面最重要的一个步骤就是如何定义解以及怎么去产生新解。 首先要注意的一点就是:在MTSP问题中起始的城市就比较关键了,我们常常将 起始的城市用编号0表示 ,剩余的城市依次用1,2,3,...,100表示,这样我们就能表示出每个旅行商的旅行顺序了。
为了方便描述,下面我们就以4个城市为例,假设这4个城市编号分别为0123,且0号为MTSP中起始的城市,再假设现在我们一共有两个旅行商,那么,我们这两个旅行商旅行方案的所有可能组合为:
3 2 1 0
3 2 0 1
3 1 2 0
3 1 0 2
3 0 2 1
3 0 1 2
2 3 1 0
2 3 0 1
2 1 3 0
2 1 0 3
2 0 3 1
2 0 1 3
1 3 2 0
1 3 0 2
1 2 3 0
1 2 0 3
1 0 3 2
1 0 2 3
0 3 2 1
0 3 1 2
0 2 3 1
0 2 1 3
0 1 3 2
0 1 2 3
这里每一行代表一种方案,我下面就挑几个方案给大家解释:
3 2 1 0:
第1个旅行商的方案:0-3-2-1-0;第2个旅行商不出门
3 2 0 1:
第1个旅行商的方案:0-3-2-0;第2个旅行商的方案:0-1-0
1 2 0 3:
第1个旅行商的方案:0-1-2-0;第2个旅行商的方案:0-3-0
1 0 2 3:
第1个旅行商的方案:0-1-0;第2个旅行商的方案:0-2-3-0
0 3 1 2:
第1个旅行商不出门;第2个旅行商的方案:0-3-1-2-0
不知道大家有没有看出来眉目,我们这里构造的解是0123的一个随机排列,并且,我们可以0作为分割点,将这个解进行划分,前面构成一个环用来描述第1个旅行商的方案,后面也构成一个环用来描述第2个旅行商的方案。(如果0的前或后没有数字则代表对应的旅行商不出门)
接下来,我们假设一共有 三个旅行商, 那么对应的解应该是怎样的呢?

先不要看下面的答案

下面揭秘答案: 此时的解应该是00123的一个随机排列,如果不考虑重复的可能,那么所有的情况一共有5!=120种:
0 0 3 2 1
0 0 3 1 2
0 0 2 3 1
0 0 2 1 3
0 0 1 3 2
0 0 1 2 3
0 3 0 2 1
0 3 0 1 2
0 3 2 0 1
0 3 2 1 0
0 3 1 0 2
0 3 1 2 0
0 2 0 3 1
0 2 0 1 3
0 2 3 0 1
0 2 3 1 0
0 2 1 0 3
0 2 1 3 0
0 1 0 3 2
0 1 0 2 3
0 1 3 0 2
0 1 3 2 0
0 1 2 0 3
0 1 2 3 0
0 0 3 2 1
0 0 3 1 2
0 0 2 3 1
0 0 2 1 3
0 0 1 3 2
0 0 1 2 3
0 3 0 2 1
0 3 0 1 2
0 3 2 0 1
0 3 2 1 0
0 3 1 0 2
0 3 1 2 0
0 2 0 3 1
0 2 0 1 3
0 2 3 0 1
0 2 3 1 0
0 2 1 0 3
0 2 1 3 0
0 1 0 3 2
0 1 0 2 3
0 1 3 0 2
0 1 3 2 0
0 1 2 0 3
0 1 2 3 0
3 0 0 2 1
3 0 0 1 2
3 0 2 0 1
3 0 2 1 0
3 0 1 0 2
3 0 1 2 0
3 0 0 2 1
3 0 0 1 2
3 0 2 0 1
3 0 2 1 0
3 0 1 0 2
3 0 1 2 0
3 2 0 0 1
3 2 0 1 0
3 2 0 0 1
3 2 0 1 0
3 2 1 0 0
3 2 1 0 0
3 1 0 0 2
3 1 0 2 0
3 1 0 0 2
3 1 0 2 0
3 1 2 0 0
3 1 2 0 0
2 0 0 3 1
2 0 0 1 3
2 0 3 0 1
2 0 3 1 0
2 0 1 0 3
2 0 1 3 0
2 0 0 3 1
2 0 0 1 3
2 0 3 0 1
2 0 3 1 0
2 0 1 0 3
2 0 1 3 0
2 3 0 0 1
2 3 0 1 0
2 3 0 0 1
2 3 0 1 0
2 3 1 0 0
2 3 1 0 0
2 1 0 0 3
2 1 0 3 0
2 1 0 0 3
2 1 0 3 0
2 1 3 0 0
2 1 3 0 0
1 0 0 3 2
1 0 0 2 3
1 0 3 0 2
1 0 3 2 0
1 0 2 0 3
1 0 2 3 0
1 0 0 3 2
1 0 0 2 3
1 0 3 0 2
1 0 3 2 0
1 0 2 0 3
1 0 2 3 0
1 3 0 0 2
1 3 0 2 0
1 3 0 0 2
1 3 0 2 0
1 3 2 0 0
1 3 2 0 0
1 2 0 0 3
1 2 0 3 0
1 2 0 0 3
1 2 0 3 0
1 2 3 0 0
1 2 3 0 0
看在我这么辛苦把这120种情况都列出的情况下,大家要不要考虑给本文点个赞~(开个玩笑,我用的是Matlab的perms函数生成的!)
接下来要对上面的解进行解释了,我们还是挑几个典型的:
3 0 2 1 0:
第1个旅行商的方案:0-3-0;第2个旅行商的方案:0-2-1-0;第3个旅行商不出门
0 1 0 3 2:
第1个旅行商不出门;第2个旅行商的方案:0-1-0;第3个旅行商的方案:0-3-2-0
1 0 3 0 2:
第1个旅行商的方案:0-1-0;第2个旅行商的方案:0-3-0;第3个旅行商的方案:0-2-0
2 0 0 3 1:
第1个旅行商的方案:0-2-0;第2个旅行商不出门;第3个旅行商的方案:0-3-1-0
0 0 3 1 2:
第1个旅行商不出门;第2个旅行商不出门;第3个旅行商的方案:0-3-1-2-0
这里我们对其解释的关键仍然是对0所在的位置进行分割,只不过这时候有两个0,我们可以根据两个0来将整个解分成三份,每一份作为一个旅行商的旅行方案,如果相应的那一份为空集的话(例如0位于最开始或最后,或者有两个0挨在一起),则认为该旅行商不出门。
上面的大家如果没有问题的话,我们来看看一个更复杂的情况:现在有21个城市,第0号为起始城市,其他城市编号为1-20,一共有4个旅行商,其中我们得到的解为:
9 19 4 10 3 0 1 15 2 0 5 7 12 18 6 11 20 8 14 0 17 13 16
那么怎么对这个解进行解释?
如果大家知道答案的话就可以继续看下面的内容啦,不知道的话建议再看看前面的内容消化消化。
前面我们说过,模拟退火里面最重要的一个步骤就是如何定义解以及怎么去产生新解,因此上面这些步骤都是告诉大家MTSP中解是如何定义的。
这里我们做一个总结:
假设现在 有n+1个城市,第0号为起始城市,其他城市编号为1至n,一共有m个旅行商,那么我们生成的解应该为:
m-1个0 和 1至n 组成的一个随机排序
注意哦,这里只有m-1个0,大家别弄错啦。这里的0你实际上就可以看成将解进行分割的位置。
那么, 我们应该如何产生新解呢? 很简单,和TSP问题一样就可以,三种方法任你挑选。
下面给大家说说编程的思路 ,事实上前面思路弄懂了应该就没问题了,只不过这里的编程还是略微有点复杂的,我提示大家一下:
(1)产生初始解的时候,我们可以先用randperm函数生成1至n的随机排序,然后再多次使用randi函数随机生成插入0的位置。
(2)计算总的距离(总成本)时,我们需要对解进行拆分,每一个旅行商经过的路径我们都可以保存在一个元胞数组中,这里面可能要用到cell函数和find函数。
后面的编程就交给大家自己实现啦,重点在于建模的思路,希望本文对大家有所启发,未来我会在购买的建模视频中给大家免费更新模拟退火,到时候有需要的话我再来详细讲解这个内容。
