牛顿迭代法是一种线性化方法,其基本思想是将非线性方程
f(x)= 0逐步归结-为某种线性方程来求解.设已知方程f(x)=0有近似根X (
假定
f’(x
k
)≠ 0),
将函数
f(x)
在点
x
k
展开,有:
f(x)≈f(x
k
)+f’(x
k
)(x-x
k
)
于是方程
f(x)=0
可近似地表示为
f(x)+ f’(x
k
)(x-x
k
)=0(
是个线性方程
)
,记其根为
x
k+1,
则
x
k+1
的计算公式为
x
k+1=
x
k
-f(x
k
)
➗
f’(x
k
)
(
k=0,1,2……
)
例题讲解
例:
用牛顿迭代法三次求方程f(x)=x
5
-x
2
+x-30=0,
在区间
[1,3]
中的近似值请详细解答
解:
f
(1)=-29
f(3)=207
所以
[1,3]
之间一定有零点。而且明显更靠近
x=3
。
f (2) =-2
f(2. 5)=63.9
f(2.2)=19.2
f(2.1)=8.53
f(2. 01)=0.78
f(2 001)=0.08
所以
f(2. 0001)=0.008
应该满足要求了。所以
x=2.0001
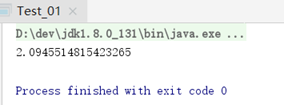
例:使用牛顿迭代法求方程的解,
X
3
-2x-5=0
,在区间
[2
,
3]上的根。
|
package
Lab_02.Test_01;
public class
Test_01 {
public static void
main(String[] args) {
double
x=
2
;
for
(
int
i=
0
;i<
20
;i++) {
x=-
f
(x)/
f1
(x)+x;
}
System.
out
.println(x+
""
);
}
static double
f(
double
x) {
double
ans;
ans=Math.
pow
(x,
3
)-
2
*x-
5
;
return
ans;
}
static double
f1(
double
x) {
double
ans;
ans=
3
*Math.
pow
(x,
2
)-
2
;
return
ans;
}
}
|
实习编辑 | 王楠岚
责 编 | 刘 连
温馨提示:
点击页面右下角
“写留言”发表评论,期待您的参与!
期待您的转发!