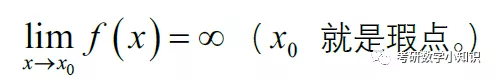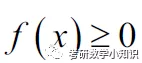a.直接计算
这种被积函数往往比较简单,容易求出其原函数,这样代入上下限就可以直接计算出积分值,也就可以一目了然判断是否收敛。
典型的有

b.利用无穷小与无穷大的知识结构
学完极限,已经知道了等价、同阶、高阶无穷小的概念,这里可以借助于这些概念,来得到另外一种判别方法——极限审敛法
对于反常积分中的被积函数
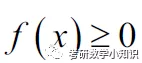
也许它很复杂,也许很简单,OK,暂时不考虑,我们只关心它跟一个被积函数的比值——该被积函数必须是简单的并且有原函数



如何判断反常积分的敛散性,在近10年来,都是以选择题的形式考察为主。主要是数一、数二在考,数三在这十年当中并没有考过一道,但是数三的考纲中是有要求的。另外,从数一、二的考题来看,考的不是什么难题,掌握住还是比较容易得分的,所以,值得引起大家的重视!1.弄清楚什么是反常积分?定积分的两个限制性条件:积分区间有限、被积函数f(x)有界也就是说,只要破坏了以上定积分的两个条件,我们所得到的积分就是反常积分!反常积分分为两类:无穷区间上的反常积分无界函数上的反常积分破坏区间的有限性 :无穷区间破坏
设函数定义在无穷区间上,且在任何有限区间上可积,如果存在极限(1)则称此极限为函数在上的无穷
反常积分
(简称无穷积分),记作并称收敛,如果极限(1)不存在,为方便起见,称发散。瑕积分
设函数定义在区间上,在点a的任一右邻域上无界,但在任何内闭区间上有界且可积,如果存在极限(2)则称此极限为无界函数在上的
反常积分
,记作,并称
反常积分
收敛,如果极限(2)不存在,
反常积分
发散,点a称...
本节介绍了无界函数的
反常积分
概念,三种无界函数
反常积分
在瑕点的极限值如果存在,则无界函数的
反常积分
存在且收敛,同样可以利用牛顿-莱布尼茨公式进行计算则无界函数的
反常积分
,否则该
反常积分
发散,无法求出。
实际上无论是无穷限函数还是无界函数,其
反常积分
如果存在,都可以通过求被积函数的原函数,然后按定义取极限,通过计算极限结合牛顿-莱布尼茨公式计算出最终结果。