for i,(images,target) in enumerate(train_loader):
    # 1. input output
    images = images.cuda(non_blocking=True)
    target = torch.from_numpy(np.array(target)).float().cuda(non_blocking=True)
    outputs = model(images)
    loss = criterion(outputs,target)
    # 2. backward
    optimizer.zero_grad()   # reset gradient
    loss.backward()
    optimizer.step()            

1. 获取loss：输入图像和标签，通过infer计算得到预测值，计算损失函数；
2. optimizer.zero_grad() 清空过往梯度；
3. loss.backward() 反向传播，计算当前梯度；
4. optimizer.step() 根据梯度更新网络参数

简单的说就是进来一个batch的数据，计算一次梯度，更新一次网络

使用梯度累加是这么写的：

for i,(images,target) in enumerate(train_loader):
    # 1. input output
    images = images.cuda(non_blocking=True)
    target = torch.from_numpy(np.array(target)).float().cuda(non_blocking=True)
    outputs = model(images)
    loss = criterion(outputs,target)
    # 2.1 loss regularization
    loss = loss/accumulation_steps   
    # 2.2 back propagation
    loss.backward()
    # 3. update parameters of net
    if((i+1)%accumulation_steps)==0:
        # optimizer the net
        optimizer.step()        # update parameters of net
        optimizer.zero_grad()   # reset gradient

1. 获取loss：输入图像和标签，通过infer计算得到预测值，计算损失函数；
2. loss.backward() 反向传播，计算当前梯度；
3. 多次循环步骤1-2，不清空梯度，使梯度累加在已有梯度上；
4. 梯度累加了一定次数后，先optimizer.step() 根据累计的梯度更新网络参数，然后optimizer.zero_grad() 清空过往梯度，为下一波梯度累加做准备；

总结来说：梯度累加就是，每次获取1个batch的数据，计算1次梯度，梯度不清空，不断累加，累加一定次数后，根据累加的梯度更新网络参数，然后清空梯度，进行下一次循环。

一定条件下，batchsize越大训练效果越好，梯度累加则实现了batchsize的变相扩大，如果accumulation_steps为8，则batchsize '变相' 扩大了8倍，是我们这种乞丐实验室解决显存受限的一个不错的trick，使用时需要注意，学习率也要适当放大。

在PyTorch中，multi-task任务一个标准的train from scratch流程为

for idx, data in enumerate(train_loader):
    xs, ys = data
    pred1 = model1(xs)
    pred2 = model2(xs)
    loss1 = loss_fn1(pred1, ys)
    loss2 = loss_fn2(pred2, ys)
    ******
    loss = loss1 + loss2
    optmizer.zero_grad()
    loss.backward()
    ++++++
    optmizer.step()

从PyTorch的设计原理上来说，在每次进行前向计算得到pred时，会产生一个 用于梯度回传的计算图，这张图储存了进行back propagation需要的中间结果，当调用了.backward()后，会从内存中将这张图进行释放

上述代码执行到******时，内存中是包含了两张计算图的，而随着求和得到loss，这两张图进行了合并， 而且大小的变化可以忽略

执行到++++++时，得到对应的grad值并且释放内存。这样，训练时必须存储两张计算图，而如果loss的来源组成更加复杂，内存消耗会更大

2. Edition2

为了减小每次的内存消耗，借助梯度累加，又有 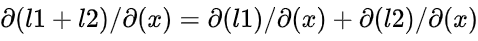，有如下变种

for idx, data in enumerate(train_loader):
    xs, ys = data
    optmizer.zero_grad()
    # 计算d(l1)/d(x)
    pred1 = model1(xs) #生成graph1
    loss1 = loss_fn1(pred1, ys)
    loss1.backward()  #释放graph1
    # 计算d(l2)/d(x)
    pred2 = model2(xs)#生成graph2
    loss2 = loss_fn2(pred2, ys)
    loss2.backward()  #释放graph2
    # 使用d(l1)/d(x)+d(l2)/d(x)进行优化
    optmizer.step()

可以从代码中看出，利用梯度累加，可以在最多保存一张计算图的情况下进行multi-task任务的训练。

另外一个理由就是在内存大小不够的情况下叠加多个batch的grad作为一个大batch进行迭代， 因为二者得到的梯度是等价的

综上可知，这种梯度累加的思路是对内存的极大友好，是由FAIR的设计理念出发的。

以上两个解释转自知乎靠前的热评回答，具体可参见 https://www.zhihu.com/question/303070254