大家在学习深度学习时,肯定会遇到softmax这个知识点,初学者大都一知半解,没有理解透彻,很多文章直接讲述softmax公式及求导,忽略了其中的因果缘由。初学者通过此文可以梳理知识结构,高手可直接查看公式推导来巩固知识。
softmax公式及理解
softmax主要用于深度学习多分类,作用是将输出层的数值映射为概率,且所有输出节点概率累加为1。
为什么要把数值转为概率呢?因为多分类模型中,输出值为概率更利于反向推导和模型的迭代(比如minist手写数字识别,对应的是0-9的概率,概率与概率可以更好的比较,数值与概率无法计算差距,从而也无法反向推导)。
接下来我们看一下softmax的公式:
如下图所示,(3,1,-3)经过softmax计算后变为概率(0.88,0.12,0),大家可以亲自计算一下,充分理解softmax公式。
求概率为什么要用e的指数?
通过e的指数图像我们可以看到:1、可以把输入为负数的值转为正数;2、指数函数曲线呈递增趋势,斜率逐渐增大,这样x轴上很小的变化反映到y轴可以看到很大的变化,所以它可以将差距大的值拉的更大。ps:其实不一定是e的指数,还有很多其他数的指数也同样适用,这里为了方便后面的计算,选用e。
补充一个知识点,softmax中,当输入值非常大时,softmax会更大,可能会溢出,所以在TensorFlow中,一般将softmax与交叉熵函数统一实现,因为TensorFlow会启用一些优化机制。
为什么softmax求导如此重要
深度学习的核心就是误差逆传播(error BackPropagation,简称BP)算法,算法中最核心的是损失函数对权重和阈值求导,在这里我们用经常与softmax使用的交叉熵损失函数为例,进行推导:
交叉熵损失函数公式(交叉熵函数中的对数,有的以e为底,有的以2为底,此处是以e为底)如下,其中
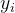 表示第i维度的实际值,
表示第i维度的实际值,
 表示第i维度的预测值:
表示第i维度的预测值:
这里我们用
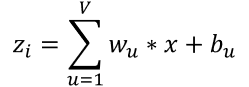 表示
表示
 的输入,v表示前一层节点的数量,
的输入,v表示前一层节点的数量,
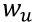 表示前一层第u个节点到
表示前一层第u个节点到
 节点的权重,
节点的权重,
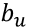 表示前一层第u个节点到
表示前一层第u个节点到
 节点的阈值。我们的目标是求
节点的阈值。我们的目标是求
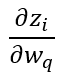 (
(
 节点对前一层第q个节点权重的偏导数)和
节点对前一层第q个节点权重的偏导数)和
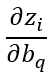 (
(
 节点对前一层第q个节点阈值的偏导数),可推导为
节点对前一层第q个节点阈值的偏导数),可推导为
根据
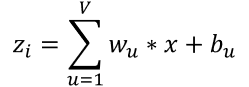 可以推导出
可以推导出
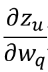 为0或x,
为0或x,
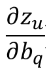 为0或1,所以当前核心问题转换为求
为0或1,所以当前核心问题转换为求
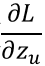 ,根据softmax公式(公式1)和 交叉熵公式(公式2),我们可以把
,根据softmax公式(公式1)和 交叉熵公式(公式2),我们可以把
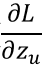 转换为:
转换为:
利用交叉熵公式(公式2),我们求L对
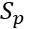 的偏导数(利用对数函数的导数公式:
的偏导数(利用对数函数的导数公式:
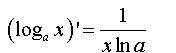 ,lne=1)可以推导出:
,lne=1)可以推导出:
有些同学对累加求导不太明白的,可以看一下知乎上的这个解释:
https://www.zhihu.com/question/67307437
,例如公式6中当i不等于p时,L对
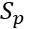 的偏导数为0,所以公式演化为
的偏导数为0,所以公式演化为
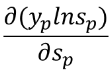 。
。
所以交叉熵对权重和阈值的求导公式只剩
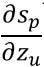 未知,即对softmax求导。
未知,即对softmax求导。
softmax求导公式推导
接下来我们对softmax求导,为了承接上面的
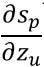 (第p个节点的softmax对u个节点的输入求偏导数),我们先用p代替softmax中的i,公式意义没有任何改变,所以softmax公式变为:
(第p个节点的softmax对u个节点的输入求偏导数),我们先用p代替softmax中的i,公式意义没有任何改变,所以softmax公式变为:
我们把softmax中的
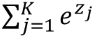 用
用
 表示(为了公式计算中书写简便,看起来更直观),则softmax公式变为:
表示(为了公式计算中书写简便,看起来更直观),则softmax公式变为:
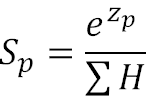
根据基本公式
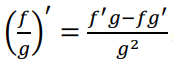 ,我们可以得到:
,我们可以得到:
当 u=p 时:
当 u!=p 时:
PS:为了避免公式中字母一样导致的歧义,我对公式上某些字母进行了修改,但公式意义没有任何改变。
扩展:交叉熵求导
家下来我们将softmax求导结果(公式6)带入交叉熵求导(公式5),可得:
将公式9和公式10带入公式11,把公式11拆分为u=p和u!=p的累加的相加,即:
接着往下推导:
到这里推导全部完成。
大家在学习深度学习时,肯定会遇到softmax这个知识点,初学者大都一知半解,没有理解透彻,很多文章直接讲述softmax公式及求导,忽略了其中的原因。初学者通过此文可以梳理知识结构,高手可直接查看公式推导来巩固知识用来面试手推。 softmax公式及理解 在深度学习反向传播算法中,为什么softmax求导如此重要 softmax求导公式推导 ...
Softmax
函数用于多分类,他将多个神经元的输出的值映射到(0,1)区间内的一个值,,并且映射的所有值相加为1,这些值可以
理解
为输出的概率,输出概率较大的一般作为预测的值
分子:fyi 表示第i个类别指数值
分母求和fj 所有元素的指数和
softmax
作用过程:假如对于神经元的输出值3,1,-3通过
softmax
函数,映射成为(0,1)之间范围的值,而这些值的累和为1,
P(3∣score)=e3/(e3+e1+e-3)=0.88
P(1∣score)=e1/(e3+e1+e-3)=0.12
P(-3∣score)=e-3/(e3+e1+e-3)=0
计算
softmax
和
row_max = x.max(axis=axis)
# 每行元素都需要减去对应的最大值,否则求exp(x)会溢出,导致inf情况
row_max = row_max.reshape(-1, 1)
x = x - row_max
# 计算e的指数次幂
x_exp = np.exp(x)
x_sum = np
(1)只对样本的硬性类别感兴趣,即属于哪个类别;
(2)希望得到软性类别,即得到属于每个类别的概率。
这两者的界限往往很模糊。其中的一个原因是,即使只关心硬类别,仍然需要使用软类别的模型。
3.4.1. 分类问题
当分类问题类别间存在自然顺序可以用数值代表每个类别,一般的分类问题并不与类别之间的自然顺序有关,可以使用独热编码。
独热编码是一个向量,它的分量和类别一样多。类别对应的分量设置为1,其他所有分量设置为0
每个激活函数的输入都是一个数字,然后对其进行某种固定的数学操作。激活函数给神经元引入了非线性因素,如果不用激活函数的话,无论神经网络有多少层,输出都是输入的线性组合。
激活函数的发展经历了Sigmoid -> Tanh -> ReLU -> Leaky ReLU ->
Maxout这样的过程,还有一个特殊的激活函数
Softmax
,因为它只会被用在网络中的最后一层,用来进行最后的分类和归一化。
Sigmoid 值范围[0,1]
输入实数值并将其“挤压”到0到1范围内,适合输出为概率.
1、多类分类和多标签分类的区别
多标签分类:一个样本可以属于多个类别(或标签),不同类之间是有关联的,比如一个文本被被划分成“人物”和“体育人物”两个标签。很显然这两个标签不是互斥的,而是有关联的
多类分类: 一个样本属于且只属于多个分类中的一个,一个样本只能属于一个类,不同类之间是互斥的,比如一个文本只能被划分成“人物”,或者被划分成“文化”,而不能同时被划分
成“人物”和“文化”,“文...
逻辑回归(Logistic Regression)是
机器学习
中的一种分类模型,由于
算法
的简单和高效,在实际中应用非常广泛。本文作为美团
机器学习
InAction系列中的一篇,主要关注逻辑回归
算法
的数学模型和参数求解方法,最后也会简单讨论下逻辑回归和贝叶斯分类的关系,以及在多分类问题上的推广。
实际工作中,我们可能会遇到如下问题:
预测一个用户是否点击特定的商品
机器学习
的问题大致可以分为分类问题和回归问题。分类问题是数据属于哪一个类别的问题。比如,区分图像中的人是男性还是女性的问题就是分类问题。而回归问题是根据某个输入预测一个(连续的)数值的问题。比如,根据一个人的图像预测这个人的体重问题是回归问题(类似“57.4kg”这样的预测)。
输出层所用的激活函数,根据求解问题的性质决定。一般,回归问题可以用恒等函数,二元分类问题可以用sigmoid函数,多元分类问题可以用
softmax
函数。
恒等函数:输出=输入
softmax
函数:输出为一个函数
其中exp
softmax
函数和sigmoid函数都是常用的激活函数,用于神经网络中的非线性变换。
softmax
函数是一种多元分类的激活函数,将多个输入值映射到一个概率分布上,使得每个输出值都在0到1之间,并且所有输出值的和为1。在神经网络中,
softmax
函数常用于输出层,用于将神经网络的输出转化为概率分布,以便进行分类任务。
sigmoid函数是一种常用的二元分类的激活函数,将输入值映射到0到1之间的一个值,表示输入值为正例的概率。在神经网络中,sigmoid函数常用于隐藏层和输出层,用于将神经元的输出转化为概率值,以便进行分类任务或回归任务。
总的来说,
softmax
函数和sigmoid函数都是常用的激活函数,用于神经网络中的非线性变换,但是它们的应用场景不同,
softmax
函数适用于多元分类任务,而sigmoid函数适用于二元分类任务。
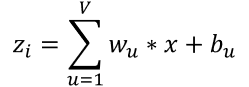 表示
表示
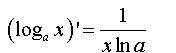 ,lne=1)可以推导出:
,lne=1)可以推导出:
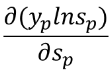
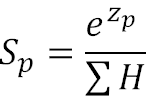
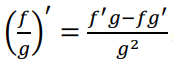 ,我们可以得到:
,我们可以得到: