2.4 基于MATLAB的地理数据重采样(空间插值)

红木棉

中山大学自然地理学本硕

本节为专栏《基于MATLAB的地理数据处理》的内容，关于该专栏的目录初步安排请戳此跳转。

本节内容所涉及到的数据、数据说明与代码文件，请到百度网盘下载。本节列出的代码均在"B4_resample.m"里。

链接： https:// pan.baidu.com/s/198G2CK ull8Nwq052FrIR5g 提取码：mian

发布时间：2022年5月26日

作者：棉

什么是重采样/空间插值（以下称为插值）？根据 Arcgis Pro文档（戳此跳转）的定义，插值指的是更改栅格数据集的空间分辨率并针对所有新像素大小的聚合值或插值设置规则。简单点说，就是我们有两套地理栅格数据，第一套数据的空间分辨率是0.3°，第二套是0.5°，为了便于比较，我们就需要将第一套数据插值到第二套数据的空间尺度（0.5°），或者将第二套数据插值到第一套数据的空间尺度（0.3°）。经过这样处理后，两套数据的矩阵大小一致，可以进行简单地加减乘除运算，或者进行更高阶的Pearson相关系数等的计算。

插值的概念又要与升/降尺度的概念区别开，这两个概念相同之处均是改变数据的空间尺度（空间分辨率），但二者之间的原理，或者说应用场景是不同的，这种不同在本节也会进行简单地介绍。

2.4.1 interp2和griddata的区别

Matlab可用于空间插值的函数有 interp2 和 griddata 两个。

（1） interp2 为interpolation 2D的缩写，即二维数据的插值，使用它的前提是数据的坐标格式必须为meshgrid格式。有阅读过本专栏《1 基于MATLAB的地理数据的读取》（戳此跳转）的读者应该知道，我们在构建数据的地理坐标网格时会用到 meshgrid 这个函数。根据官方文档的说法，meshgrid格式的意思如以下例子所示：

[X,Y] = meshgrid(x,y) 
% 基于向量 x 和 y 中包含的坐标返回二维网格坐标。
% X 是一个矩阵，每一行是 x 的一个副本；Y 也是一个矩阵，每一列是 y 的一个副本。
% 坐标 X 和 Y 表示的网格有 length(y) 个行和 length(x) 个列。

其实大部分地理数据的经纬度或者横纵坐标网格都是meshgrid格式的，可以直接用 interp2 进行插值。此外， interp2 函数的运算速度较快。

（2） griddata 函数也可用于地理数据插值，但是被插值的数据坐标格式没必要是meshgrid格式的。因此， griddata 函数可以用来将一些随机分布的点数据插值至规则网格，亦或是将MODIS的正弦投影数据（该投影坐标网格不是meshgrid格式）插值至规则网格。与 interp2 函数相比， griddata 函数运算速度较慢，因此如果数据是meshgrid格式的，那就都用 interp2 函数吧！

interp2 函数的用法主要如下所示：

Vq = interp2(X, Y, V, Xq, Yq, method)

很明显，输入变量有用来插值的数据V及其对应的坐标X、Y，以及我们所要插值到的坐标Xq、Yq，如果不输入method的话默认为'linear'法。最终输出变量Vq即插值后的数据值。

2.4.2 插值方法的简单介绍

插值方法中，比较常用的主要是以下两种（摘抄自Argis Pro文档）：

（1）最邻近（nearest）

将使用最近邻技术。因为没有新值创建，此方法可将像素值的更改内容最小化，这是最快的重采样技术。适用于离散数据，例如土地覆被。

（2）双线性（linear）

将使用双线性插值技术。可采用平均化（距离权重）周围 4 个像素的值计算每个像素的值。适用于连续数据。

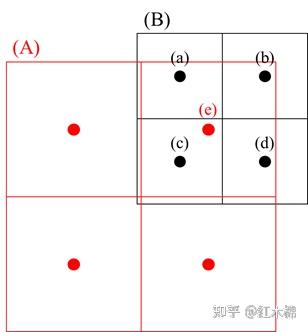
如图1所示，空间尺度为B的数据插值到空间尺度为A的数据，最邻近法便是将c数据插值到e点，双线性插值法便是通过对a、b、c、d四个数据值进行平均化后赋值到e点。

注意：最邻近法中，如果c数据为NaN值，则插值后的e数据为NaN；双线性法中，如果a、b、c、d有至少一个数据为NaN值的话，插值后的e数据也为NaN。

接下来将以两个案例说明 interp2 函数在重采样（空间插值）中的应用。

2.4.3 案例1——空间数据重采样(插值)为点数据

本案例介绍如何将地理栅格数据插值至一个坐标点上，应用场景主要是利用点尺度的实地观测数据对空间尺度的遥感数据进行对比验证。本案例以GPM降水数据为例，使用珠三角的国家级气象站点的气象观测数据对GPM进行评估。

首先读取气象站点数据，并将小时尺度的气象数据合并为日尺度的数据：

% 读取txt格式的气象数据
data1 = readtable('.\Data\table_CMA_DATA\DATA_CMA_CHN_MUL_HOR.txt');
% 读取txt格式的气象站点位置数据
loc = readtable('.\Data\table_CMA_DATA\Location_Station.txt');
% 提取出站点经纬度
lon1 = loc.Longitude;
lat1 = loc.Latitude;
% 对4月13日的降水数据进行提取并合成为日尺度
data_station = nan(21,2);
data_station(:,1) = data1.Station_ID(1:144:3024); % 第一列为21个站点
interval = 73:144:3024;
for ii = 1:21
    data_station(ii,2) = sum(data1.PRE_1h_mm(interval(ii):interval(ii)+23)); % 第二列为4月13日降水

接下来读取GPM降水数据：

% 读取4月13日的GPM_IMERG降水数据
data2 = ncread('.\Data\nc_GPM\3B-DAY-E.MS.MRG.3IMERG.20220413-S000000-E235959.V06.nc4', 'precipitationCal'); % Variables
lon2 = ncread('.\Data\nc_GPM\3B-DAY-E.MS.MRG.3IMERG.20220413-S000000-E235959.V06.nc4', 'lon');
lat2 = ncread('.\Data\nc_GPM\3B-DAY-E.MS.MRG.3IMERG.20220413-S000000-E235959.V06.nc4', 'lat');
lat2 = flipud(lat2);
[lon2, lat2] = meshgrid(lon2, lat2);

最后，使用interp2函数，使用最邻近法将GPM栅格降水数据插值到气象站点：

data_interp = interp2(lon2, lat2, data2, lon1, lat1, 'nearest');

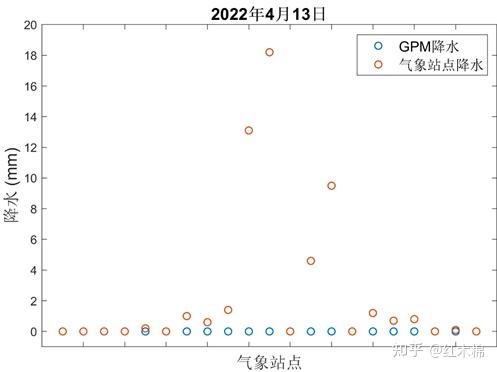
将GPM插值后的data_interp与站点降水数据data_station对比可发现（图2），4月13日当天部分站点有降水记录，但GPM在所有站点的降水量都为0，表明GPM降水在这一天的表现不好。

2.4.4 案例2——空间数据重采样(插值)为空间数据

本案例介绍如何将地理栅格数据插值至另一个坐标网格的地理上额数据，应用场景主要是：（1）不同空间分辨率的地理栅格数据的比较；（2）将所有地理数据统一到一个空间分辨率，以方便结合起来进行应用分析。本案例以36 km空间分辨率的SMAP L3土壤水分数据与0.25°空间分辨率的AMSRU土壤水分数据为例，介绍如何对空间数据进行插值（重采样）。

首先读取SMAP土壤水分数据并进行质量处理，数据读取与质量处理可看《2.3 基于MATLAB的卫星遥感数据产品的质量处理(Quality Flag)》（戳此跳转）：

% SMAP L3 土壤水分数据
data_smap = h5read('.\Data\h5_SMAP\SMAP_L3_SM_P_20200705_R18290_002.h5',...
        '/Soil_Moisture_Retrieval_Data_AM/soil_moisture');
lon_smap = h5read('.\Data\h5_SMAP\SMAP_L3_SM_P_20200705_R18290_002.h5',...
        '/Soil_Moisture_Retrieval_Data_AM/longitude'); 
lat_smap = h5read('.\Data\h5_SMAP\SMAP_L3_SM_P_20200705_R18290_002.h5',...
        '/Soil_Moisture_Retrieval_Data_AM/latitude'); 
data_smap = data_smap'; lon_smap = lon_smap'; lat_smap = lat_smap';
% 数值范围 & 缺失值 (Valid Min & Fill/Gap Value)
data_smap(data_smap<0.02) = nan; % Valid Min
data_smap(data_smap==-9999)= nan; % Fill/Gap Value
% 反演质量评估(Retrieval Quality Flag)
sm_q = h5read('.\Data\h5_SMAP\SMAP_L3_SM_P_20200705_R18290_002.h5',...
        '/Soil_Moisture_Retrieval_Data_AM/retrieval_qual_flag');
sm_q = sm_q';
data_smap( ~(sm_q==0 | sm_q==8) ) = nan;

注意：由于SMAP土壤水分NaN值出现的点的坐标也为NaN值，因此读取出的lat_smap和lon_smap网格包含NaN值，不是严格意义的meshgrid格式矩阵，因此我们需重新构建经纬网格。

% SMAP土壤水分NaN值出现的点的坐标也为NaN值，因此需重新构建经纬网格
lat_smap(lat_smap==-9999) = nan;
lat_smap = unique(lat_smap); 
lat_smap(isnan(lat_smap)) = []; 
lat_smap = flipud(lat_smap);
lon_smap(lon_smap==-9999) = nan;
lon_smap = unique(lon_smap);
lon_smap(isnan(lon_smap)) = []; 
lon_smap = lon_smap';
[lon_smap, lat_smap] = meshgrid(lon_smap, lat_smap);

接下来读取AMSRU土壤水分数据，这里涉及到投影坐标转换为地理坐标的内容，具体可看《2.1 基于MATLAB的坐标系转换(投影坐标转为经纬坐标)》（戳此跳转）：

% 读取AMSRU土壤水分数据
[data_amsru, R] = readgeoraster('.\Data\tiff_AMSRU\AMSRU_Mland_2020187D_v03.tif');
% AMSRU读取出的数据是个三维矩阵，第三维中第6页数据为土壤水分数据
data_amsru = data_amsru(:,:,6); 
X = R.XWorldLimits(1)+0.5*R.CellExtentInWorldX : R.CellExtentInWorldX : R.XWorldLimits(2)-0.5*R.CellExtentInWorldX; % 计算出X坐标
Y = R.YWorldLimits(2)-0.5*R.CellExtentInWorldX : -R.CellExtentInWorldX : R.YWorldLimits(1)+0.5*R.CellExtentInWorldX; % 计算出Y坐标
[X, Y] = meshgrid(X, Y);