用Python实现数字孪生【含源码】
在这个教程中,我们将展示如何用 Python 创建简单但实用的数字孪生,锂离子电池将是我们的实物资产。这个数字孪生将使我们能够分析和预测电池行为,并且可以集成到任何虚拟资产管理工作流程中。我们将使用Keras建立神经网络,使用plotly绘图。
1、虚拟系统和数字孪生
数字孪生是工业4.0的重要组成部分,其基本原则是在虚拟世界中复现实物资产,以模拟其动态。想象一下,我们在城市的水管网的某个地方有一个水泵。水泵消耗能量,以水流和压力的形式释放能量。术语"复现"是指创建能够模拟此行为的虚拟对象。
这个泵与管道、阀门、仪表和其他配件或子系统,都是整个水管网系统的一部分。这些子系统彼此连接。虚拟化一个系统需要对所有子系统执行相同的工作。之后,我们可以模拟整个系统,包括其依赖性。虚拟系统的目标是模仿物理世界,以便引入更改、评估性能或预测涉及此资产或子系统的场景(例如在维护任务中)。
如前所述,数字孪生体是代表子系统的虚拟对象。这个"孪生"应该以与"物理孪生"相同的方式响应输入变量。此虚拟对象必须集成模型才能做到这一点。数字孪生最重要的特点是模型可以模拟数字环境中的"物理"行为。请记住,当我们说"物理",我们指的是任何现实世界的实体(可以是一个锂离子电池,水泵,一个人,一个城市或一只猫)。任何可以建模的东西都可以虚拟化:

2、锂离子电池的数字模型
可充电锂离子电池是一种尖端的电池技术,其电化学中依赖锂离子。除了便携式技术设备外,这些电池也是电动汽车和配电网络中用于储能等应用的重要资产。这些电池最关键的方面是它们的老化成本。重复充电放电周期后,电池会退化,导致充电容量降低。这种现象一直是开发耐用电池的关键研究领域。其建模同样是一个有争议的话题。电池退化对上述技术的规划和运营有重要影响。
电池寿命退化的物理原理相当复杂。近年来,有人提出一些半经验性质的锂离子电池退化模型,用于测量电池寿命损失。废电池通常被描述为只提供其额定最大容量的 80% 的电池。此退化可以使用以下经验模型描述:
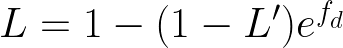
其中 L 是电池寿命时间,L'是初始电池寿命时间,fd 是单位时间和周期的线性退化率 。该速率是 放电时间 t 、 放电周期深度δ的 、 电荷 周期平均状态 σ 和单元温度 Tc的函数:
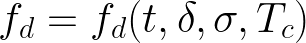
3、实验数据
我们的模型必须基于已经掌握的信息预测电池的寿命。但是,我们想将此模型与为确定模型的准确性而进行的测量进行比较。让我们在这里暂停一下。
许多数字孪生不是基于精确的物理模型。他们只使用实验数据集和机器学习算法。这是一种很酷的做事方法。例如,他们可以使用深度神经网络模型来捕获数据的真实动态。但是,将此模型推广到其他对象需要与大量数据集配合工作,才能获得可靠的通用模型。另一方面,在物理模型工作时,我们需要更少的数据来获得准确的通用模型。
我们将利用锂离子电池充放电周期的真实数据来构建我们的数字孪生体。我们将使用美国宇航局的数据集(锂离子电池老化数据集)。此数据收集来自美国宇航局Ames预知中心自建的电池预后测试站 (PCoE)。此数据集对于确定我们物理模型的准确性和改进其价值。我们将使用与电池 5 号相关的数据。我们将绘制 "容量" 功能与周期数,并将其与我们的物理模型进行比较。在我们开始之前,我们将变量L( 电池寿命 )替换为 C(电池容量 )。方程 1 将写如下:
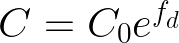
其中 C 是电池容量 ,C0 是初始电池容量。对于 fd, 我们使用了以下近似:
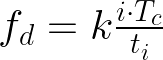
其中i是放电周期,tc在周期内在测量的电池cell温度,ti是放电时间,k是经验常数,值取 0.13。

图2说明了结果。我们的模型准确地预测了观测到的值(平均绝对误差为0.004)。该模型应收集电池容量行为,其中容量在第一个周期中缓慢下降,然后在特定点后加速。这些变化是微妙的,许多工程师使用简单的线性模型来接近这种行为。我们的模型是半经验性的,包括各种调整,以避免处理偏 微分方程 。
4、构建混合数字孪生
我们可以直接使用"模型"创建一个数字孪生。但是,为了应用机器学习,我们将使用它在美国宇航局数据集的实验数据的基础上改进模型使用。方案见下图。

我们利用实验数据和神经网络模型的输出来改进模型。
#Define inputs and outputs
# input: the simulation capacity
X_in = (dfb['C. Capacity'])
# output: difference between experimental values and simulation
X_out = (dfb['Capacity']) - (dfb['C. Capacity'])
X_in_train, X_in_test, X_out_train, X_out_test = train_test_split(X_in, X_out, test_size=0.33)我们使用的是非常简单的神经网络:
model = Sequential()
model.add(Dense(64, activation='relu', input_shape=(1,)))
model.add(Dense(32, activation='relu'))
model.add(Dense(1))整合:
epochs = 100
loss = 'mse'
model.compile(optimizer = SGD(learning_rate=0.001),
loss=loss,
metrics=['mae'], #Mean Absolute Error
history = model.fit(X_in_train,
X_out_train,
