Python代码:递归实现C4.5决策树生成、剪枝、分类
系列文章:
Python代码:递归实现ID3决策树生成、剪枝、分类
Python代码:处理连续、离散特征的朴素贝叶斯分类
Python代码:基于KD树实现K近邻分类、回归(KNN)
支持向量机分类算法推导:从原始问题到对偶问题
Python代码:梯度下降法/SMO算法实现支持向量机分类(SVM)
Python代码:梯度下降法/SMO算法实现支持向量机回归(SVR)
Python代码:SMO算法实现支持向量数据描述(SVDD)
Python代码:SMO算法实现单类支持向量机(OC-SVM)
现尝试使用Python编程实现 C4.5决策树(C4.5 decision tree) 分类算法,使用Numpy进行矩阵运算。 程序代码附于本文最后,也可直接从Github下载更完整的、最新的代码:
欢迎收藏(Stars)、点赞。
参考资料
[1] 周志华. 机器学习 [M]. 清华大学出版社, 2016. 第4章 决策树.
[2] Peter Harrington. Machine Learning in Action [M]. Manning Publications Co., 2012. Chapter 3 Splitting datasets one feature at a time: decision trees.
[3] 李航. 统计学习方法 (第2版) [M]. 清华大学出版社, 2019. 第5章 决策树.
1 算法原理
决策树可用于分类和回归。上一篇文章介绍了用于分类的ID3决策树( Python代码:递归实现ID3决策树生成、剪枝、分类 )。 C4.5决策树是对ID3决策树的改进。 ID3算法按照“最大化信息增益”的准则来选择最优的划分特征,然而这对可取值数目较多的离散值特征有所偏好(即:若按可取值数目较多的离散值特征来划分样本集,则划分所得的子样本集可达到更小的信息熵,所获得的信息增益也必然较大)。为了减小这种偏好引起潜在的不利影响,C4.5决策树不直接使用信息增益,而使用“信息增益率”来选择最优划分特征。确切而言, C4.5算法按照“先从候选划分特征中找出信息增益高于平均水平的特征,再从中选择信息增益率最高者”的方法来选择最优划分特征。
如何由训练样本集生成C4.5决策树?如何对新样本进行分类?对此,与 介绍ID3决策树的文章 类似,将以一个简单的数据集为例进行说明。
如下,这是一个具有12个样本、每个样本有4个特征的训练样本集。其中,特征1、特征2、特征3的取值是离散的,特征4的取值是连续的。
| 特征1(风向) | 特征2(湿度) | 特征3(紫外线指数) | 特征4(温度℃) | 类别标签 | |
|---|---|---|---|---|---|
| 训练样本1 | 东 | 干燥 | 强 | 33 | 晴天 |
| 训练样本2 | 南 | 潮湿 | 强 | 31 | 晴天 |
| 训练样本3 | 北 | 适中 | 强 | 35 | 晴天 |
| 训练样本4 | 西 | 适中 | 强 | 26 | 晴天 |
| 训练样本5 | 南 | 潮湿 | 弱 | 24 | 阴天 |
| 训练样本6 | 西 | 干燥 | 强 | 27 | 阴天 |
| 训练样本7 | 西 | 潮湿 | 强 | 30 | 阴天 |
| 训练样本8 | 东 | 适中 | 弱 | 22 | 阴天 |
| 训练样本9 | 南 | 适中 | 弱 | 22 | 雨天 |
| 训练样本10 | 北 | 潮湿 | 弱 | 20 | 雨天 |
| 训练样本11 | 东 | 适中 | 弱 | 29 | 雨天 |
| 训练样本12 | 西 | 潮湿 | 弱 | 24 | 雨天 |
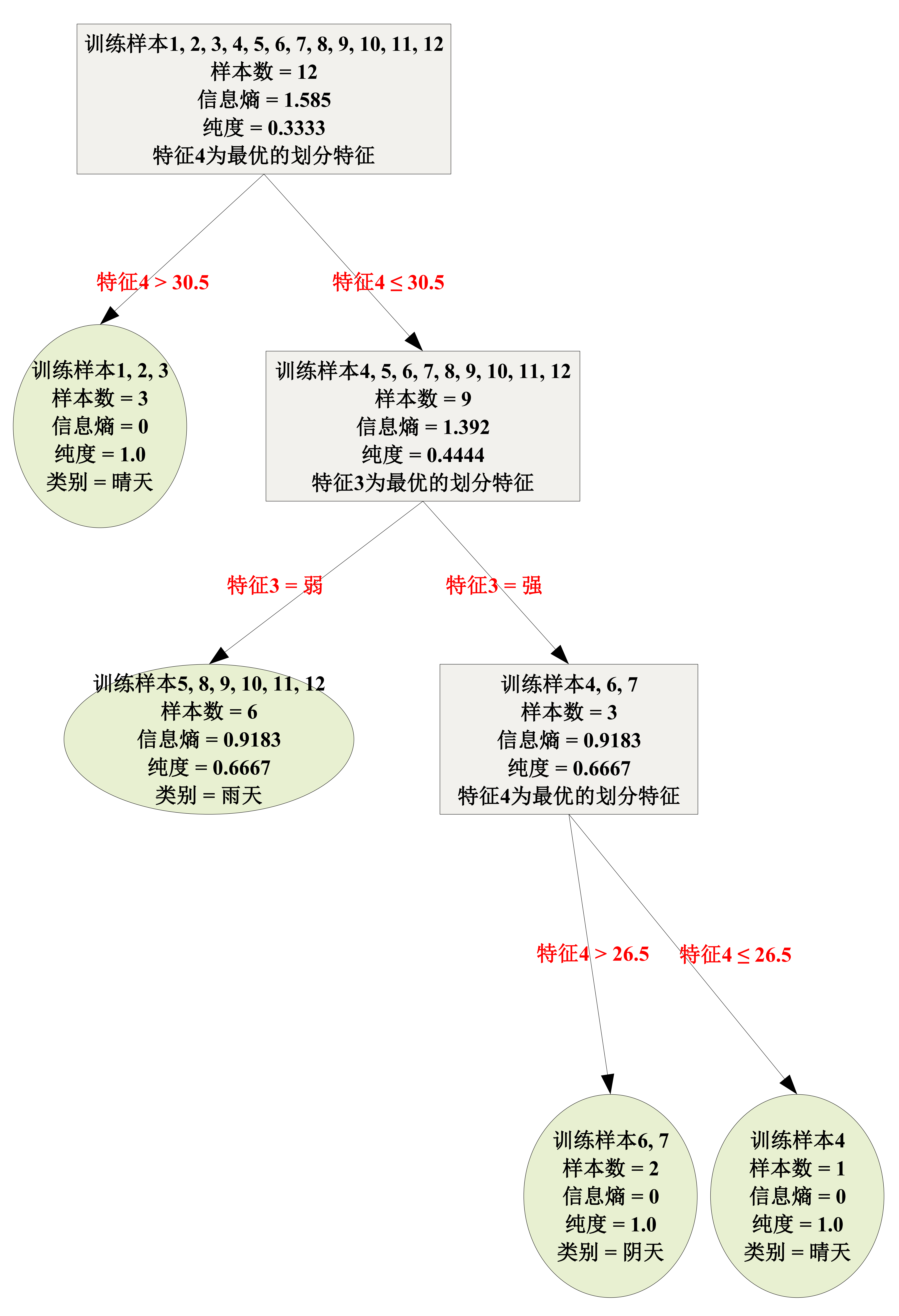
如何由该训练样本集生成C4.5决策树?先放上结果,下图即为由C4.5算法生成的决策树。自上而下分布的灰色矩形与绿色椭圆称为“结点”。 绿色椭圆称为“叶结点”,对应于分类结果,不含有下级子结点;灰色矩形称为“内部结点”,含有下级子结点;最顶的内部结点也称为“根结点”,包含所有12个训练样本。
1.1 如何预测新样本的类别?
例如,对于一个新样本 [东, 潮湿, 弱, 20],即特征1(风向)为“东”、特征2(湿度)为“潮湿”、特征3(紫外线指数)为“弱”、特征4(温度)为20℃,该样本没有在训练样本集中出现过,那么其所属类别为晴天、阴天还是雨天?
根据生成的C4.5决策树,
自上而下作出判别
:
首先,从根结点出发,因为新样本的特征4取值为20℃,其小于30.5℃,故进入根结点的右子结点(它是一个内部结点);
然后,因为新样本的特征3取值为“弱”,故进入当前内部结点的左子结点(它也是一个内部结点);
接着,因为新样本的特征1取值为“东”,故进入当前内部结点的最左子结点(它也是一个内部结点);
最后,因为新样本的特征4取值20℃,其小于25.5℃,故进入当前内部结点的右子结点,即抵达类别为“阴天”的叶结点,从而将新样本归类为“阴天”。
1.2 如何由训练样本集生成C4.5决策树?
回到问题“如何由训练样本集生成C4.5决策树”。具体而言,如何将每一个内部结点所包含的样本集划分至子结点? C4.5算法按照“先从候选划分特征中找出信息增益高于平均水平的特征,再从中选择信息增益率最高者”的方法来选择最优划分特征 ;根据所选最优划分特征的取值的不同,将原样本集划分成2个(或2个以上)子样本集。
信息熵(Information entropy)的定义:
对于一个样本集 D ,第 k 类样本所占的比例为 p_k\;(k=1,2,...,K) , K 为该样本集的类别数,则样本集 D 的信息熵为 \mathrm{Entropy}(D) = -\sum_{k=1}^{K}{p_k\operatorname{log}_2 p_k}\\ \mathrm{Entropy}(D) 值越小,则样本集 D 所包含的样本越趋同于一个类别,即 D 的纯度越高。
对于某个离散值特征,它有 V 个可能的取值 \{\mathrm{Value}_1,\mathrm{Value}_2,...,\mathrm{Value}_V\} ,若使用该特征对样本集 D 进行划分,则会生成 V 个子样本集 \{D_1,D_2,...,D_V\} ,对应地属于 V 个子结点。其中,子样本集 D_v 包含了 D 中在划分特征上取值为 \mathrm{Value}_v 的样本。
对于某个连续值特征,由于可取值的数目是无限的,故不能根据特征的可取值来划分样本集 D 。可采用二分法(Bi-partition)处理连续值特征:先提取该连续值特征在样本集 D 上的取值,并剔除重复值,则得到 n 个不同的取值,将这些值从小到大排序,记为 \{\mathrm{Value}_1,\mathrm{Value}_2,...,\mathrm{Value}_n\} ,则可得到 n-1 个候选划分点 t_i = \frac{\mathrm{Value}_i+\mathrm{Value}_{i+1}}{2},\;\;\;\;i=1,2,...,n-1\\ 也即将区间 [\mathrm{Value}_{i},\mathrm{Value}_{i+1}) 的中位点作为候选划分点。基于任意一个划分点 t_i 都可以将样本集 D 二分为子样本集 D_{t_i,+} 和 D_{t_i,-} 。子样本集 D_{t_i,+} 包含在划分特征上取值大于 t_i 的样本;子样本集 D_{t_i,-} 包含在划分特征上取值不大于 t_i 的样本。
信息增益(Information gain)的定义:
以某个特征对样本集 D 进行划分所获得的信息增益 \mathrm{Gain}(D,某个特征)=\mathrm{Entropy}(D)-\sum_{v=1}^{V}{\frac{\left| D_v \right|}{\left| D \right|}}\mathrm{Entropy}(D_v)\\ 其中, \left| D \right| 为样本集 D 的样本数; \left| D_v \right| 为子样本集 D_v 的样本数; V 为划分得到的子样本集的数量。
特别地,若划分特征为连续值特征,子样本集的数量 V=2 ,则 \begin{align} &\mathrm{Gain}(D,某个连续值特征)\\ &=\mathrm{Entropy}(D)-\left[\frac{\left| D_{t_i,+} \right|}{\left| D \right|}\mathrm{Entropy}(D_{t_i,+})+\frac{\left| D_{t_i, -} \right|}{\left| D \right|}\mathrm{Entropy}(D_{t_i, -})\right]\\ \end{align}\\
进一步,定义信息增益率。
信息增益率(Information gain ratio)的定义:
\mathrm{GainRatio}(D,某个特征)=\frac{\mathrm{Gain}(D,某个特征)}{\mathrm{IV}(D,某个特征)}\\ 其中 \mathrm{IV}(D,某个特征)=-\sum_{v=1}^{V}{\frac{\left| D_v \right|}{\left| D \right|}\operatorname{log}_2 \frac{\left| D_v \right|}{\left| D \right|}}\\ 称为固有值(Intrinsic value)。 \left| D \right| 为样本集 D 的样本数; \left| D_v \right| 为子样本集 D_v 的样本数; V 为划分得到的子样本集的数量。
特别地,若划分特征为连续值特征,子样本集的数量 V=2 ,则 \mathrm{IV}(D,某个连续值特征)=-\left[\frac{\left| D_{t_i,+} \right|}{\left| D \right|}\operatorname{log}_2 \left(\frac{\left|D_{t_i,+} \right|}{\left| D \right|}\right)+\frac{\left| D_{t_i,-} \right|}{\left| D \right|}\operatorname{log}_2 \left(\frac{\left|D_{t_i,-} \right|}{\left| D \right|}\right)\right]\\
C4.5算法通过遍历样本集的所有候选特征,按照“先从候选划分特征中找出信息增益高于平均水平的特征,再从中选择信息增益率最高者”的方法来选择最优的划分特征。以最顶内部结点(即根结点)为例进行说明,根结点包含所有12个训练样本,记为样本集 D ,其信息熵
\begin{align} \mathrm{Entropy}(D) &= -\sum_{k=1}^{K}{p_k\operatorname{log}_2 p_k}\\ &=-\left[\frac{4}{12} \times \operatorname{log}_2 \left(\frac{4}{12}\right) +\frac{4}{12} \times \operatorname{log}_2 \left(\frac{4}{12}\right)+\frac{4}{12} \times \operatorname{log}_2 \left(\frac{4}{12}\right)\right]\\ &\approx 1.585 \end{align}\\
若选取特征1(风向)进行划分,特征1为离散值特征,有4个可能的取值(东、南、西、北),则4个子样本集分别含有3、3、4、2个样本,4个子样本集的信息熵分别为1.585、1.585、1.5、1。以特征1对训练样本集 D 进行划分所获得的信息增益 \begin{align} \mathrm{Gain}(D,特征1)&=\mathrm{Entropy}(D)-\sum_{v=1}^{V}{\frac{\left| D_v \right|}{\left| D \right|}}\mathrm{Entropy}(D_v)\\ &\approx1.585-\left(\frac{3}{12} \times 1.585+ \frac{3}{12} \times 1.585+\frac{4}{12} \times 1.5+\frac{2}{12} \times 1\right)\\ &\approx0.126 \end{align}\\
以特征1对训练样本集 D 进行划分的固有值 \begin{align} \mathrm{IV}(D,特征1)&=-\sum_{v=1}^{V}{\frac{\left| D_v \right|}{\left| D \right|}\operatorname{log}_2 \frac{\left| D_v \right|}{\left| D \right|}}\\ &=-\left[\frac{3}{12} \times \mathrm{log}_2 \left(\frac{3}{12} \right) +\frac{3}{12} \times \mathrm{log}_2 \left(\frac{3}{12}\right) +\frac{4}{12} \times \mathrm{log}_2 \left(\frac{4}{12}\right) +\frac{2}{12} \times \mathrm{log}_2 \left(\frac{2}{12}\right) \right]\\ &\approx 1.959 \end{align}\\
若选取特征2(湿度)进行划分,特征2为离散值特征,有3个可能的取值(干燥、潮湿、适中),则3个子样本集分别含有2、5、5个样本,3个子样本集的信息熵分别为1、1.522、1.522。以特征2对训练样本集 D 进行划分所获得的信息增益 \begin{align} \mathrm{Gain}(D,特征2)&=\mathrm{Entropy}(D)-\sum_{v=1}^{V}{\frac{\left| D_v \right|}{\left| D \right|}}\mathrm{Entropy}(D_v)\\ &=1.585-\left(\frac{2}{12} \times 1+ \frac{5}{12} \times 1.522+\frac{5}{12} \times 1.522\right)\\ &\approx0.150 \end{align}\\
以特征2对训练样本集 D 进行划分的固有值 \begin{align} \mathrm{IV}(D,特征2)&=-\sum_{v=1}^{V}{\frac{\left| D_v \right|}{\left| D \right|}\operatorname{log}_2 \frac{\left| D_v \right|}{\left| D \right|}}\\ &=-\left[\frac{2}{12} \times \mathrm{log}_2 \left(\frac{2}{12} \right) +\frac{5}{12} \times \mathrm{log}_2 \left(\frac{5}{12}\right) +\frac{5}{12} \times \mathrm{log}_2 \left(\frac{5}{12}\right) \right]\\ &\approx 1.483 \end{align}\\
若选取特征3(紫外线指数)进行划分,特征3为离散值特征,有2个可能的取值(强、弱),则2个子样本集分别含有6、6个样本,2个子样本集的信息熵分别为0.9183、0.9183。以特征3对训练样本集 D 进行划分所获得的信息增益 \begin{align} \mathrm{Gain}(D,特征3)&=\mathrm{Entropy}(D)-\sum_{v=1}^{V}{\frac{\left| D_v \right|}{\left| D \right|}}\mathrm{Entropy}(D_v)\\ &\approx1.585-\left(\frac{6}{12} \times 0.9183+ \frac{6}{12} \times 0.9183\right)\\ &\approx0.667 \end{align}\\
以特征3对训练样本集 D 进行划分的固有值 \begin{align} \mathrm{IV}(D,特征3)&=-\sum_{v=1}^{V}{\frac{\left| D_v \right|}{\left| D \right|}\operatorname{log}_2 \frac{\left| D_v \right|}{\left| D \right|}}\\ &=-\left[\frac{6}{12} \times \mathrm{log}_2 \left(\frac{6}{12} \right) +\frac{6}{12} \times \mathrm{log}_2 \left(\frac{6}{12}\right) \right]\\ &= 1 \end{align}\\
若选取特征4(温度)进行划分,特征4为连续值特征,在样本集 D 上的取值为33、31、35、26、24、27、30、22、22、20、29、24,剔除重复值并按照从小到大排序,则得到20、22、24、26、27、29、30、31、33、35,共10个取值。于是,得到9个划分点:21、23、25、26.5、28、29.5、30.5、32、34。分别使用这9个划分点将样本集 D 分成2个子样本集,计算出对应的信息增益。通过对比9个划分点,得知划分点30.5可达到最大信息增益。此时,在特征4上取值大于30.5的子样本集含有3个样本,在特征4上取值不大于30.5的子样本集含有9个样本,这2个子样本集的信息熵分别为0、1.392。于是,以特征4对训练样本集 D 进行划分所获得的信息增益 \begin{align} \mathrm{Gain}(D,特征4)&=\mathrm{Entropy}(D)-\sum_{v=1}^{V}{\frac{\left| D_v \right|}{\left| D \right|}}\mathrm{Entropy}(D_v)\\ &\approx1.585-\left(\frac{3}{12} \times 0+ \frac{9}{12} \times 1.392\right)\\ &\approx0.541 \end{align}\\
以特征4对训练样本集 D 进行划分的固有值 \begin{align} \mathrm{IV}(D,特征4)&=-\sum_{v=1}^{V}{\frac{\left| D_v \right|}{\left| D \right|}\operatorname{log}_2 \frac{\left| D_v \right|}{\left| D \right|}}\\ &=-\left[\frac{3}{12} \times \mathrm{log}_2 \left(\frac{3}{12} \right) +\frac{9}{12} \times \mathrm{log}_2 \left(\frac{9}{12}\right) \right]\\ &\approx 0.8113 \end{align}\\
逐一计算4个特征的信息增益率:
以特征1对训练样本集 D 进行划分所获得的信息增益率 \mathrm{GainRatio}(D,特征1)=\frac{\mathrm{Gain}(D,特征1)}{\mathrm{IV}(D,特征1)}\approx\frac{0.126}{1.959}\approx0.064\\
以特征2对训练样本集 D 进行划分所获得的信息增益率 \mathrm{GainRatio}(D,特征2)=\frac{\mathrm{Gain}(D,特征2)}{\mathrm{IV}(D,特征2)}\approx\frac{0.150}{1.483}\approx0.10\\
以特征3对训练样本集 D 进行划分所获得的信息增益率 \mathrm{GainRatio}(D,特征3)=\frac{\mathrm{Gain}(D,特征3)}{\mathrm{IV}(D,特征3)}\approx\frac{0.667}{1}\approx0.67\\
以特征4对训练样本集 D 进行划分所获得的信息增益率 \mathrm{GainRatio}(D,特征4)=\frac{\mathrm{Gain}(D,特征4)}{\mathrm{IV}(D,特征4)}\approx\frac{0.541}{0.8113}\approx0.67\\
因为4个特征的平均信息增益为 \frac{0.126+0.150+0.667+0.541}{4}=0.371 ,其中特征3的信息增益0.667、特征4的信息增益0.541高于平均信息增益,所以选择特征3、特征4二者当中信息增益率最大者作为最优划分特征。又因为特征3、特征4的信息增益率相等,故随机选择了特征4(温度)作为最优划分特征。根结点按特征4划分出2个子结点。
同理,对于根结点的子结点,也按照上述方法选取最优的划分特征,进而划分出下级子结点,直到满足成为叶结点的条件(见1.3 及早停止树的生长)。注意, 若内部结点所包含的样本集在某个特征上只有1个取值,则不可再选取该特征用于划分。
1.3 及早停止树的生长
在上述例子中,生成的C4.5决策树的每一个叶结点都是纯的(只含有1种类别的样本),且只包含1个样本。这会导致决策树模型十分复杂,容易对训练样本过拟合。所有叶结点都是纯的,意味着决策树在训练样本集上的预测准确率是100%,但在测试样本集上的预测准确率很可能极其不佳。
为了防止过拟合,可设置条件将划分出的某些子结点强制记为叶结点,从而使决策树及早停止生长。可设置以下超参数:
-
叶结点的最少样本数量:
当划分出的子结点所含样本的数量少于或等于一定值时,则将该结点记为叶结点。 -
最大树深:
当树生长的深度达到一定值时,则将当前结点记为叶结点。需指出,根结点的深度为0,根结点的子结点的深度为1,根结点的子结点的子结点的深度为2,依此类推。 -
叶结点的最大纯度:
当划分出的子结点的纯度大于或等于一定值时,则将该结点记为叶结点。结点纯度的定义: \mathrm{purity}=\operatorname{max}(p_1, p_2, ...,p_K)\\ 其中, p_k 为第 k 类样本所占的比例, K 为结点所包含样本集的类别数。
当叶结点的纯度不足1时,即存在多个类别的样本,则取最多数类别(众数)作为叶结点的类别。若存在2个或2个以上的类别并列作为最多数类别,则可从中随机选择一个作为叶结点的类别。
1.4 剪枝
防止过拟合的另一种方法是先生成决策树,随后删除信息量很少的叶结点,即将这些叶结点的父结点作为新的叶结点,称为“后剪枝”(Post-pruning)或“剪枝”(Pruning)。 剪枝是对满足“全部子结点皆为叶结点”的内部结点所尝试执行的操作。
此处与前一篇文章《 Python代码:递归实现ID3决策树生成、剪枝、分类 》相同,Python程序使用“代价复杂度剪枝”(Cost complexity pruning)。
代价复杂度剪枝:
针对一个内部结点,假设它的子结点均为叶结点,则判断是否执行剪枝。定义剪枝前的损失函数 L_{\mathrm{before}}=\sum_{t=1}^{T}{N_t \cdot \mathrm{Entropy}(D_t)}+\alpha T\\ 其中, T 为叶结点数目; N_t 为第 t 叶结点所包含的样本数; D_t 表示第 t 叶结点所包含的样本集; \mathrm{Entropy}(D_t) 为第 t 叶结点所包含的样本集的信息熵; \alpha \;(\alpha\geq0) 为超参数,较大的 \alpha 促使得到更简单的决策树(叶结点更少), \alpha=0 意味着仅追求最大化决策树与训练样本的拟合程度,不考虑决策树的复杂度。
定义剪枝后的损失函数 L_{\mathrm{after}}=N \cdot \mathrm{Entropy}(D)+\alpha\\ 其中, N 为剪枝前所有叶结点的样本数之和,即 N=\sum_{t=1}^{T}{N_t} ; D 表示内部结点所包含的样本集,也是各个叶结点所含样本集 D_1,D_2,...,D_T 的并集;剪枝后,由于 T 个叶子结点“回缩”到父结点,成为1个新的叶结点,故第2加数项为 \alpha \times1 ,即 \alpha 。
若 L_{\mathrm{after}} \leq L_{\mathrm{before}} ,则执行剪枝,即删除 T 个叶子结点,将它们的父结点(剪枝前的内部结点)作为新的叶结点;否则,不执行剪枝。
以本文训练样本集生成的C4.5决策树为例,进一步描述如何实现剪枝。
取参数 \alpha=2.5 ,尝试对下图当中“剪刀”标示的内部结点进行剪枝。

计算剪枝前的损失函数值 \begin{align} L_{\mathrm{before}}&=\sum_{t=1}^{T}{N_t \cdot \mathrm{Entropy}(D_t)}+\alpha T\\ &=\left(1 \times 0+1 \times 0 \right)+2.5 \times 2\\ &=5 \end{align}\\ 计算剪枝后的损失函数值
\begin{align} L_{\mathrm{after}}&=N \cdot \mathrm{Entropy}(D)+\alpha\\ &=2 \times 1+2.5\\ &=3.5\\ \end{align}\\ 显然, L_{\mathrm{after}}<L_{\mathrm{before}} ,所以执行剪枝。剪枝后的决策树如下图。
进一步针对所有满足“全部子结点皆为叶结点”的内部结点,计算剪枝前和剪枝后的损失函数值,判断是否执行剪枝,最终得到完全剪枝的决策树,如下图。
2 程序代码简介
- 变量命名遵循3个习惯: Python机器学习代码变量命名的说明 。
- 尽量为每一行代码添加中文注释。
-
算法封装成类C45decisionTree。实例化时,可给定下列超参数:
叶结点的最少样本数量 minSamplesLeaf;
最大树深 maxDepth;
叶结点的最大纯度 maxPruity;
最大特征数 maxFeatures;
代价复杂度剪枝的惩罚参数 α。 -
实例化类C45decisionTree之后,调用 .fit(X__, y_, indexContinuousFeatures_=()) 方法进行训练,即生成C4.5决策树;
X__为存储训练样本特征向量的矩阵,可以有离散值特征和连续值特征;
y_存储各个训练样本的类别标签;
indexContinuousFeatures_为可选参数,表示训练样本的连续值特征的序号,例如:
.fit(X__, y_, indexContinuousFeatures_=(0, 2, 5)) 表示指出训练样本的第0、第2、第5特征为连续值特征。 注意,此处从0开始数数。
若不指定indexContinuousFeatures_,则默认值为空元组(),表示所有特征均为离散值特征。 - 调用 .pruning() 方法进行后剪枝,本程序使用“代价复杂度剪枝”。
- 调用 .predict(X__) 方法进行测试,即对测试样本矩阵X__的各个样本进行分类。
3 运行示例
使用本文的简单天气数据集进行试验,先训练(生成)C4.5决策树,随后剪枝,最后对4个新样本分类。运行结果:
>>>
使用天气数据集进行试验...
给定第(3,)特征为连续值特征
执行代价复杂度剪枝,惩罚参数:α = 2.5
剪枝前,C4.5决策树的叶结点总数:9
剪枝后,C4.5决策树的叶结点总数:4
训练样本集的测试正确率:0.8333
预测新样本 ['东' '潮湿' '弱' '20'] 的类别为 "雨天"
预测新样本 ['南' '干燥' '强' '34'] 的类别为 "晴天"
预测新样本 ['北' '干燥' '强' '26'] 的类别为 "晴天"
预测新样本 ['南' '干燥' '弱' '20'] 的类别为 "雨天"4 Python程序代码
分为2个.py文件:C45决策树分类.py、决策树工具函数.py。
其中,“C45决策树分类.py”是主程序,可直接一键运行。
“C45决策树分类.py”文件的代码:
# C45决策树分类.py
from typing import Optional, Sequence
from numpy import ndarray, array, unique, log2, inf
from numpy.random import choice
from 决策树工具函数 import entropy, purity, majority, \
splitDataset_forDiscreteFeature, \
biPartitionDataset_forContinuousFeature
class C45decisionTree:
"""C4.5决策树分类"""
def __init__(self,
minSamplesLeaf: int = 1, # 超参数:叶结点的最少样本数量
maxDepth: int = 7, # 超参数:最大树深
maxPruity: float = 1., # 超参数:叶结点的最大纯度
maxFeatures: Optional[int] = None, # 超参数:最大特征数
α: float = 0., # 超参数:代价复杂度剪枝的惩罚参数
assert type(minSamplesLeaf)==int and minSamplesLeaf>0, '叶结点的最少样本数量minSamplesLeaf应为正整数'
assert type(maxDepth)==int and maxDepth>0, '最大树深maxDepth应为正整数'
assert 0<maxPruity<=1, '叶结点的最大纯度maxDepth的取值范围应为(0, 1]'
assert (maxFeatures is None) or (type(maxFeatures)==int and maxFeatures>0), '最大特征数maxFeatures应为正整数,或不给定maxFeatures'
assert α>=0, '代价复杂度剪枝的惩罚参数α应为非负数'
self.minSamplesLeaf = minSamplesLeaf # 超参数:叶结点的最少样本数量
self.maxDepth = maxDepth # 超参数:最大树深
self.maxPruity = maxPruity # 超参数:叶结点的最大纯度
self.maxFeatures = maxFeatures # 超参数:最大特征数
self.α = α # 超参数:代价复杂度剪枝的惩罚参数
self.M = None # 输入特征向量的维数
self.tree = None # 字典:树
self.indexContinuousFeatures_ = None # 数组索引:连续值特征的序号
def fit(self,
X__: ndarray,
y_: ndarray,
indexContinuousFeatures_: Sequence[int] = (), # 数组索引:连续值特征的序号
"""训练"""
assert type(X__)==ndarray and X__.ndim==2, '输入训练样本矩阵X__应为2维ndarray'
assert type(y_)==ndarray and y_.ndim==1, '输入训练标签y_应为1维ndarray'
assert len(X__)==len(y_), '输入样本数量应等于标签数量'
self.M = X__.shape[1] # 输入特征向量的维数
self.indexContinuousFeatures_ = tuple(indexContinuousFeatures_) # 数组索引:连续值特征的序号
if self.indexContinuousFeatures_:
print(f'给定第{self.indexContinuousFeatures_}特征为连续值特征')
if self.maxFeatures is None:
self.maxFeatures = self.M # 若未指定最大特征数maxFeatures,则默认设置为特征总数M
assert self.maxFeatures<=self.M, f'最大特征数maxFeatures不应大于输入特征向量的维数{self.M},当前 maxFeatures = {self.maxFeatures}'
indexFeatureCandidates_ = array(range(self.M)) # 数组索引:所有候选特征的序号
self.tree = self.createTree(X__, y_, indexFeatureCandidates_=indexFeatureCandidates_) # 生成树
return self
def createTree(self,
X__: ndarray, y_: ndarray,
indexFeatureCandidates_: ndarray, # 数组索引:所有候选的特征的序号
depth: int = 0, # 当前树深
) -> dict:
"""递归地生成C4.5分类树"""
结点的结构,字典:
'class label' : 结点的类别标签,
'number of samples' : 结点的样本数量,
'entropy' : 结点的熵值,
'purity': 结点的纯度,
'index of splitting feature' : 划分特征的序号,
'partition point' : 划分点,
'child nodes' : {'划分特征的取值1' : 子结点,
'划分特征的取值2' : 子结点,
当结点的划分特征为离散值特征时,无'partition point'键值对;
当结点的划分特征为离散值特征时,'划分特征的取值1'、'划分特征的取值2'、'划分特征的取值3'、……等,分别为划分特征的各个离散取值;
当结点的划分特征为连续值特征时,'划分特征的取值1'和'划分特征的取值2'分别为'+'和'-',分别指示划分特征取值大于、不大于划分点的子结点;
当结点为叶结点时,无'child nodes'、'index of splitting feature'、'partition point'等键值对。
N = len(X__) # 样本数目
p = purity(y_) # 纯度
"""创建结点"""
node = {'class label': majority(y_), # 记录:结点类别
'number of samples': N, # 记录:结点样本数量
'entropy': entropy(y_), # 记录:结点熵值
'purity': p, # 记录:结点纯度
if (len(set(y_))==1 or # 若该结点是纯的(所有类别标签都相同),则返回叶结点
len(indexFeatureCandidates_)==0 or # 若所有特征已被用于划分,则返回叶结点
depth>=self.maxDepth or # 若达到最大树深,则返回叶结点
N<=self.minSamplesLeaf or # 若达到叶结点的最少样本数量,则返回叶结点
p>=self.maxPruity or # 若达到叶结点的最大纯度,则返回叶结点
len(unique(X__, axis=0))==1 # 若所有样本特征向量都相同,则返回叶结点
return node
"""选择最优的划分特征"""
result = self.chooseBestFeature(X__, y_, indexFeatureCandidates_)
if
type(result)==tuple:
# 若result是一个元组,则选择了一个连续值特征序号和对应的最优划分点
mBest, tBest = result[0], result[1]
else:
# 若result是一个数,则选择了一个离散值特征序号
mBest = result
"""创建子结点"""
node['index of splitting feature'] = mBest # 记录:最优划分特征的序号
depth += 1 # 树深+1
if mBest in self.indexContinuousFeatures_:
# 若第mBest特征是连续值特征,则按最优划分点tBest,二分样本集
node['partition point'] = tBest # 记录:最优划分点
node['child nodes'] = {} # 初始化子结点
Xhigher__, Xlower__, yHigher_, yLower_ = \
biPartitionDataset_forContinuousFeature(X__=X__, y_=y_, m=mBest, t=tBest) # 二分样本集
node['child nodes']['+'] = \
self.createTree(Xhigher__, yHigher_, indexFeatureCandidates_, depth) # 创建第mBest特征取值大于tBest的子结点
node['child nodes']['-'] = \
self.createTree(Xlower__, yLower_, indexFeatureCandidates_, depth) # 创建第mBest特征取值不大于tBest的子结点
else:
# 若第mBest特征是离散值特征,则按第mBest特征的所有离散取值划分样本集
indexFeatureCandidates_ = indexFeatureCandidates_[indexFeatureCandidates_!=mBest] # 剔除已被用于划分的离散值特征
values_ = unique(X__[:, mBest]) # 第mBest特征的所有取值
node['child nodes'] = {} # 初始化子结点
for value in values_:
# 遍历最优划分特征的所有取值,分别创建子结点
Xsubset__, ySubset_ = \
splitDataset_forDiscreteFeature(X__=X__, y_=y_, m=mBest, value=value) # 划分出子样本集
node['child nodes'][value] = \
self.createTree(Xsubset__, ySubset_, indexFeatureCandidates_, depth) # 创建第mBest特征取值为value的子结点
return node
def chooseBestFeature(self, X__: ndarray, y_: ndarray,
indexFeatureCandidates_: ndarray):
"""选择最优的划分特征:输入样本集X_、标签y_,输出最优特征序号 mBest"""
N = len(X__) # 样本数量
baseEntropy = entropy(y_) # 样本集的信息熵
for m in indexFeatureCandidates_.copy():
if len(set(X__[:, m]))==1:
# 若第m特征只有1个取值,则剔除该特征,不能选该特征进行划分
indexFeatureCandidates_ = indexFeatureCandidates_[indexFeatureCandidates_!=m]
Nfeatures = min(self.maxFeatures, len(indexFeatureCandidates_)) # 特征子集的特征数量
indexFeaturesChosen_ = choice(indexFeatureCandidates_, Nfeatures, replace=False) # 数组索引:随机选取的特征子集的序号
informationGains_ = {} # 初始化字典:{ 选取的特征的序号: 按该特征划分所获得的信息增益}
gainRatio_ = {} # 初始化字典:{ 选取的特征的序号: 按该特征划分所获得的信息增益率}
indexBestPartitionPoint_ = {} # 初始化字典:{ 选取的连续值特征的序号: 该连续值特征的最优划分点}
for m in indexFeaturesChosen_:
# 遍历所有选取的特征,计算按各特征划分所获得的信息增益和信息增益率
values_ = unique(X__[:, m]) # 第m特征所有的取值(剔除重复值)
if m in self.indexContinuousFeatures_:
# 若第m特征为连续值特征
values_ = values_.astype(float) # 将第m特征的取值转化为浮点型
values_.sort() # 升序排列第m特征的取值
t_ = (values_[:-1] + values_[1:])/2 # 划分点序列
informationGains_[m] = -1e100 # 初始化:按第m特征划分所获得的信息增益
for t in t_:
# 遍历第m特征的所有划分点,找到最优划分点
Xhigher__, Xlower__, yHigher_, yLower_ = \
biPartitionDataset_forContinuousFeature(X__=X__, y_=y_, m=m, t=t) # 按划分点t划分成2个子样本集
pHigher = len(yHigher_)/N # 第m特征取值大于t的子样本集所占比例
pLower = len(yLower_)/N # 第m特征取值不大于t的子样本集所占比例
newEntropy = pHigher*entropy(yHigher_) + pLower*entropy(yLower_) # 2个子样本集的熵值
informationGain = baseEntropy - newEntropy # 信息增益
if informationGain > informationGains_[m]:
indexBestPartitionPoint_[m] = t # 记录:第m特征的最优划分点
informationGains_[m] = informationGain # 记录:第m特征的最大信息增益
IV = -(pHigher*log2(pHigher) + pLower*log2(pLower)) # 记录:第m特征的最优划分点的固有值
else:
# 若第m特征为离散值特征
newEntropy = 0. # 初始化:按第m特征划分得到的多个子样本集的熵值
IV = 0. # 初始化:固有值
for value in values_:
# 遍历第m特征所有的取值
Xsubset__, ySubset_ = \
splitDataset_forDiscreteFeature(X__=X__, y_=y_, m=m, value=value) # 划分出子样本集
p = len(ySubset_)/N # 第m特征取值为value的样本所占比例
newEntropy += p*entropy(ySubset_) # 多个子样本集的熵值
IV += -p*log2(p) # 计算样本集关于第m特征的固有值
informationGains_[m] = baseEntropy - newEntropy # 按第m特征划分所获得的信息增益
gainRatio_[m] = inf if IV==0 else (informationGains_[m]/IV) # 按第m特征划分所获得的信息增益率
"""选择最优的特征"""
# C4.5算法:从信息增益高于平均水平的特征中选择信息增益率最大者
averageInformationGain = sum([informationGains_[key] for key in informationGains_])/\
len(informationGains_) # 平均信息增益
indexHighGainFeatures_ = [] # 初始化数组索引:信息增益高于平均水平的特征序号
for m in informationGains_:
# 遍历所有选取的特征,找出信息增益高于平均水平的特征序号
if informationGains_[m]>averageInformationGain:
indexHighGainFeatures_.append(m) # 数组索引:信息增益高于平均水平的特征序号
if len(indexHighGainFeatures_)==0:
# 若找不到任何一个“信息增益高于平均水平”的特征,是因为每个特征的信息增益都相等,
# 浮点运算误差也有可能导致计算得到的平均信息增益averageInformationGain略大于每个选取特征的信息增益。
# 此时,每一个选取的特征都是“信息增益等于平均水平”的特征,随后可从中选出信息增益率最大者进行划分
indexHighGainFeatures_ = indexFeaturesChosen_ # 数组索引:信息增益高于(或等于)平均水平的特征序号
maxGainRatio = 0. # 初始化最大信息增益率
for m in indexHighGainFeatures_:
# 遍历所有“信息增益高于(或等于)平均水平”的特征,找出信息增益率最大的特征序号
if gainRatio_[m]>maxGainRatio:
maxGainRatio = gainRatio_[m] # 记录:最大信息增益率
mBest = m # 记录:最优的划分特征
if mBest in self.indexContinuousFeatures_:
# 若最优的划分特征是连续值特征,则返回特征序号和最优划分点
tBest = indexBestPartitionPoint_[mBest] # 最优划分点
return mBest, tBest
else:
# 若最优的划分特征是离散值特征,则仅返回特征序号
return mBest
def classify(self, node: dict, x_: ndarray):
"""递归地确定样本x_的类别:输入1个样本x_,输出预测类别"""
if 'child nodes' not in node:
# 若当前结点不含'child nodes'键,则该结点为叶结点,返回叶结点的类别标签
y = node['class label']
else:
# 若当前结点是内部结点,则继续进入下级子结点
m = node['index of splitting feature'] # 当前结点以第m特征进行划分
if m in self.indexContinuousFeatures_:
# 若第m特征是连续值特征
t = node['partition point'] # 读取划分点
if x_[m].astype(float)>t:
childNode = node['child nodes']['+'] # 进入第m特征取值大于划分点t的子结点
else:
childNode = node['child nodes']['-'] # 进入第m特征取值不大于划分点t的子结点
else:
# 若第m特征是离散值特征
for value in node['child nodes'].keys():
# 遍历当前结点第m特征的取值
if x_[m]==value:
childNode = node['child nodes'][value] # 进入第m特征取值为value的子结点
break
else:
# 若当前结点无x_[m]这个取值的子结点,返回当前结点的类别标签
y = node['class label']
return y
y = self.classify(childNode, x_) # 进入子结点
return y
def pruning(self):
"""剪枝"""
print(f'执行代价复杂度剪枝,惩罚参数:α = {self.α}')
print(f'剪枝前,C4.5决策树的叶结点总数:{self.countLeafNumber(self.tree)}')
self.tree = self.costComplexityPruning(self.tree) # 剪枝
print(f'剪枝后,C4.5决策树的叶结点总数:{self.countLeafNumber(self.tree)}')
return self
def costComplexityPruning(self, node):
"""递归地执行代价复杂度剪枝"""
for key in node['child nodes']:
# 对所输入的内部结点,遍历其各个子结点
if 'child nodes' in node['child nodes'][key]:
# 若子结点含有键'child nodes',则该结点是内部结点,可尝试剪枝
node['child nodes'][key] = self.costComplexityPruning(node['child nodes'][key])
# 判断当前结点node的所有子结点是否为叶结点
nodeIsLeaf_ = [('child nodes' not in node['child nodes'][key])
for key in node['child nodes']] # 若当前结点node的某个子结点不含有下一级子结点,则该子结点为叶结点
"""若当前根结点的所有子结点都是叶结点,尝试剪枝"""
if all(nodeIsLeaf_):
# 若当前结点node的所有子结点都是叶结点,尝试剪枝
lossBeforePruning = 0. # 初始化:剪枝前的损失函数值
for key in node['child nodes']:
# 遍历所有叶结点
entropy = node['child nodes'][key]['entropy'] # 叶结点的熵值
N = node['child nodes'][key]['number of samples'] # 叶结点的样本数量
lossBeforePruning += entropy*N # 剪枝前的损失函数值
lossBeforePruning += self.α*len(nodeIsLeaf_) # 剪枝前的损失函数
lossAfterPruning = node['number of samples']*node['entropy'] + self.α # 剪枝后的损失函数
if lossAfterPruning <= lossBeforePruning:
# 若剪枝后的损失函数值小于或等于剪枝前的损失函数值,则剪枝
del node['child nodes'] # 删除键'child nodes',内部结点变成叶结点
del node['index of splitting feature']
if 'partition point' in node:
del node['partition point']
return node
def countLeafNumber(self, node: dict) -> int:
"""计算结点(树)的叶结点数"""
if 'child nodes' not in node:
# 若结点node无'child nodes'键,则其为叶结点
number = 1
else:
# 若结点node有'child nodes'键,则其为内部结点
number = 0
for key in node['child nodes']:
# 遍历内部结点的子结点
number += self.countLeafNumber(node['child nodes'][key])
return number
def predict(self, X__: ndarray) -> ndarray:
"""测试"""
assert type(X__)==ndarray and X__.ndim==2, '输入测试样本矩阵X__应为2维ndarray'
assert X__.shape[1]==self.M, f'输入测试样本特征向量维数应等于训练样本特征向量维数{self.M}'
y_ = [self.classify(self.tree, x_) for x_ in X__] # 对样本逐个进行分类
y_ = array(y_)
return y_
def accuracy(self, X__: ndarray, y_: ndarray) -> float:
"""计算测试正确率"""
测试正确样本数 = sum(self.predict(X__)==y_)
总样本数 = len(y_)
return
测试正确样本数/总样本数
if __name__=='__main__':
import numpy as np
# 设置随机种子
from numpy.random import seed; seed(0)
from random import seed; seed(0)
print('使用天气数据集进行试验...\n')
天气数据集 = np.array([
# 风向 湿度 紫外线指数 温度 类别标签
['东', '干燥', '强', 33, '晴天'],
['南', '潮湿', '强', 31, '晴天'],
['北', '适中', '强', 35, '晴天'],
['西', '适中', '强', 26, '晴天'],
['南', '潮湿', '弱', 24, '阴天'],
['西', '干燥', '强', 27, '阴天'],
['西', '潮湿', '强', 30, '阴天'],
['东', '适中', '弱', 22, '阴天'],
['南', '适中', '弱', 22, '雨天'],
['北', '潮湿', '弱', 20, '雨天'],
['东', '适中', '弱', 29, '雨天'],
['西', '潮湿', '弱', 24, '雨天'],
Xtrain__ = 天气数据集[:, :-1] # 样本特征向量矩阵
ytrain_ = 天气数据集[:, -1] # 样本标签
indexContinuousFeatures_ = (3,) # 连续值特征的序号
# 实例化C4.5决策树模型
model = C45decisionTree(
minSamplesLeaf=1, # 超参数:叶结点的最少样本数量
maxDepth=7, # 超参数:最大树深
maxPruity=1., # 超参数:叶结点的最大纯度
# maxFeatures=4, # 超参数:最大特征数
α=2.5, # 超参数:代价复杂度剪枝的惩罚参数
model.fit(Xtrain__, ytrain_,
indexContinuousFeatures_=indexContinuousFeatures_, # 连续值特征的序号
) # 训练
model.pruning() # 剪枝
print(f'训练样本集的预测正确率:{model.accuracy(Xtrain__, ytrain_):.4f}\n')
Xtest__ = np.array([['东', '潮湿', '弱', 20],
['南', '干燥', '强', 34],
['北', '干燥', '强', 26],
['南', '干燥', '弱', 20]]) # 测试样本集
ytest_ = model.predict(Xtest__) # 测试样本集的预测结果
for x_, y in zip(Xtest__, ytest_):
print(f'预测新样本 {x_} 的类别为 "{y}"') # 显示预测结果
“决策树工具函数.py”文件的代码:
# 决策树工具函数.py
from numpy import ndarray, array, zeros, unique, log2
def biPartitionDataset_forDiscreteFeature(
X__: ndarray, # 样本特征向量矩阵
y_: ndarray, # 样本标签
m: int, # 特征序号
value, # 第m特征的某个取值
对离散值特征,二分样本集:
将原始样本集X__、标签集y_,按照第m特征的取值是否为value,划分为2个子集
logicYes_ = X__[:, m]==value # 逻辑索引:第m特征的取值是value的样本
logicNo_ = ~logicYes_ # 逻辑索引:第m特征的取值非value的样本
# 提取第m特征取值是value的样本
Xyes__ = X__[logicYes_]
yYes_ = y_[logicYes_]
# 提取第m特征取值非value的样本
Xno__ = X__[logicNo_]
yNo_ = y_[logicNo_]
return Xyes__, Xno__, yYes_, yNo_
def biPartitionDataset_forContinuousFeature(
X__: ndarray, # 样本特征向量矩阵
y_: ndarray, # 样本标签
m: int, # 特征序号
t: float, # 第m特征的划分点
对连续值特征,二分样本集:
将原始样本集X__、标签集y_,按照第m特征的取值是否大于t,划分为2个子集
logicHigher_ = X__[:, m].astype(float)>t # 逻辑索引:第m特征的取值大于t的样本
logicLower_ = ~logicHigher_ # 逻辑索引:第m特征的取值不大于t的样本
# 提取第m特征的取值大于t的样本
Xhigher__ = X__[logicHigher_]
yHigher_ = y_[logicHigher_]
# 提取第m特征的取值不大于t的样本
Xlower__ = X__[logicLower_]
yLower_ = y_[logicLower_]
return Xhigher__, Xlower__, yHigher_, yLower_
def splitDataset_forDiscreteFeature(
X__: ndarray, # 样本特征向量矩阵
y_: ndarray, # 样本标签
m: int, # 特征序号
value, # 第m特征的某个取值
对离散值特征,划分出子样本集:
提取原始样本集X__、标签集y_当中第m特征取值是value的子样本集
values_ = X__[:, m] # 提取第m特征的取值
# 提取第m特征的取值是value的样本
Xsubset__ = X__[values_==value]
ySubset_ = y_[values_==value]
return Xsubset__, ySubset_
def entropy(y_: ndarray) -> float:
"""输入类别标签集y_,输出信息熵"""
N = len(y_) # 样本数量
classes_ = unique(y_) # 所有类别标签
K = len(classes_) # 类别数
N_ = zeros(K) # 各类别的样本数量
for k, c1ass in enumerate(classes_):
# 遍历K个类别,计算各类别的样本数量
N_[k] = sum(y_==c1ass) # 第k类别的样本数量
p_ = N_/N # 所有类别的样本数量占总样本数的比例
s = -log2(p_).dot(p_) # 信息熵
return s
def gini(y_: ndarray) -> float:
"""输入类别标签集y_,输出基尼指数gini"""
N = len(y_) # 样本数量
classes_ = unique(y_) # 所有类别标签
K = len(classes_) # 类别数
N_ = zeros(K) # 各类别的样本数量
for k, c1ass in enumerate(classes_):
# 遍历K个类别,计算各类别的样本数量
N_[k] = sum(y_==c1ass) # 第k类别的样本数量
p_ = N_/N # K维向量:K个类别的样本在样本集所占比例
gini = 1 - sum(p_**2)
return gini
def purity(y_: ndarray) -> float:
"""输入标签集y_,输出纯度"""
N = len(y_) # 样本数量
classes_ = unique(y_) # 所有类别标签
K = len(classes_) # 类别数
N_ = zeros(K) # 各类别的样本数量
for k, c1ass in enumerate(classes_):
# 遍历K个类别,计算各类别的样本数量
N_[k] = sum(y_==c1ass) # 第k类别的样本数量
p_ = N_/N # 所有类别的样本在总体样本集所占比例
return p_.max()
def majority(y_):
"""输入标签集y_,输出占多数的类别(众数)"""
y_ = array(y_) # 转化为ndarray
assert y_.ndim==1, '输入标签集y_应可转化为1维ndarray'
classes_ = unique(y_) # 所有类别标签
K = len(classes_) # 类别数
