【深度学习之美27】循序神经网络(RNN)到底是个什么东东?
14.1 你可能不具备的一种思维
吴京主演的电影《战狼 Ⅱ》大获好评。走进电影院的你,如痴如醉,外加一把爱国泪,绝不肯错过冷锋的每一个镜头。
假设情况不是这样,仅想打发无聊时光的你,随机选择了一部电影,不凑巧,电影是一部烂片,电影播到10分钟20分钟时,你会怎么办?
是当机立断地拂袖而去呢?
还是强打精神看下去(毕竟电影票花了80块人民币啊)?
在经济学领域,有个重要的概念,叫“沉没成本”。
说的就是, 有选择就有成本,没有选择就没有成本 。当我们没办法再做选择时,就不存在成本,这是著名论断“ 沉没成本不是成本 ”的含义。
要知道,一旦电影开播,影城绝不会退给你票款,因此,这80块就属于你付出的“沉没成本”。如果你真的能践行“沉没成本不是成本”的话,那么你的最佳决策应该是立马走人。
可问题是,又有几人能做到?
是的,能践行这个论断的,只属于理性经济人,它不属于正常人。包括经济学家在内的绝大多数人,离开理论假设,在现实生活中,真的很难无视“沉没成本”。
其实,很多学科都是相同的。如果用计算机术语来说,上面的含义可以表述为,人们真的很难采用马尔科夫链思维。
所谓马尔科夫链,通俗来讲,就是未来的一切,仅与当前有关,而与历史无关。人们常说 “要活在当下”,其实这是很难做到的,因为通常人们的每一个决策,都是基于历史行为和当前状态叠加作用下做出的。

因此,有人就说,不管是李世石,还是柯洁,他们不仅是败在计算机的“数据”、“算法”和“算力”上,而且还败在思维方式上。因为人类不具备马尔科夫链思维(图14-1)。
也就是说,人类不可避免地要受到历史的影响,人们善于追求前后一致,首尾协调,逻辑一贯。换句话说,人类的行为通常是历史的产物、习惯的奴隶。
而阿尔法狗在棋盘上的表现,发挥稳定,且时有跳脱之举。原因很简单,这些“机器”狗在下每一步棋时,都能做到,以当下的棋局视为起点,过往不究,不受历史逻辑一贯性的指引及与之相伴的约束。
那么,现在问题来了。这“过往”的历史,到底是“究”好呢,还是“不究”好呢?我们知道,虽然这些“机器狗”们下棋能力很强,但仍然属于弱人工智能(Artificial Narrow Intelligence,ANI)范畴。不然的话,你让阿尔狗给婴儿换个纸尿裤试试?
弱人工智能进一步的发展方向,自然就是强人工智能(Artificial General Intelligence,AGI)。所谓强人工智能,就是那种能够达到人类级别的人工智能。目前人工智能的现状,可以用一句话概括:“ 强在弱人工智能,弱在强人工智能。 ”
强、弱人工智能的一个重要差别就在于,弱人工智能不具备很多“常识”。而所谓“常识”,就是常见的知识,它是人类历史经验的一种凝结。比如,你向天空抛一个皮球,一两岁的小婴儿都知道它会落下来(常识),然后等它落地之后,再屁颠屁颠地去追皮球。而这些领域之外的常识,阿尔法狗是不具备的。
如果你认可“人类智能”,还是强过当前机器的“人工智能”的话,你就知道前面问题的答案了:这过往的“历史”还是究得好,因为历史是未来前进的基石!
既然还是人类的大脑好使,既然历史在人类决策中有重要作用,既然人工神经网络是对生物神经网络模拟,那么,当前有没有哪种人工神经网络,能模拟人脑利用历史信息来做决策呢?
当然有!这就是我们本章要讲的主题“循环神经网络(Recurrent Neural Network,RNN)”。
看到这儿,或许你都乐了,饶了这么大的圈子,就为引入这个主题啊。
是的,我就是想告诉你,倘若论下围棋,阿尔法狗稳操胜券胜。但倘若从差异性很强的领域穿越,纵横捭阖,套路深的那个,还是作为人类的我啊!
14.2 何谓RNN?
玩笑完毕,言归正传。谈到RNN,这里需要讲明,它其实是两种不同神经网络的缩写。一种是时间递归神经网络(recurrent neural network),另一种是结构递归神经网络(recursive neural network)。请注意,很多文献也分别将它们称为“循环神经网络”和“递归神经网络”。在下文中,如果不特别注明,在提及RNN时,指的是“时间递归神经网络”,即“循环神经网络”。
在前面章节讨论的神经网络模型(如卷积神经网络),都无法利用历史数据的时间依赖关系,来分析数据特征,从而可能导致对当前和未来产生一些不合理的预测。
但在很多实际应用中,数据之间是存在相互依赖关系的。例如,当我们在思考问题时,我们都是在已有经验和知识的基础之上,再结合当前实际情况综合给出决策,而不会把过往的经验和记忆都“弃之若敝”。
比如说,在《战狼 Ⅱ》中,当那个中美混血的漂亮女主角一出现,后面的情节即使不看,我们大致也能预测到,无非是“英雄救美女,美女爱英雄”。看到最后,果不其然。如果连这都猜不到,那我们过去那么多电影也就白看了。

再比如,如果我们试图预测一下“天空飞过一只__”这句话最后一个词是什么?利用前面输入的一连串的历史信息:“天 空 飞 过 一 只”,我们就能大致猜出最后一个词可能是“小鸟”也可能是“蜻蜓”之类的飞行动物,但定然不是能是“人”或“坦克”(常识告诉我们,人和坦克都不能飞),当然也不能“猪”(即使可能是风口中的猪,但量词“只”也把它过滤掉了)。
由此可见,历史对于我们推测未来,是极有帮助的,不可轻易抛弃。而RNN的核心诉求之一,就是能将以往的信息连接到当前任务之中。
追根溯源,RNN最早是由Hopfiled网络启发变种而来[1]。Hopfiled网络是1982年由约翰·霍普菲尔德提出的网络结构,此类网络内部有反馈连接,能够处理信号中的时间依赖性。1
986年,Michael Jordan(他可不是那位NBA篮球之神,而是著名机器学习大师、深度学习大咖吴恩达的导师)借鉴了Hopfiled网络的思想,首次在神经网络中引入循环连接[2]。
1990年,Jeffrey Elman又在Jordan的研究基础上,正式提出了RNN模型,不过那时RNN还叫SRN (Simple Recurrent Network,简单循环网络)[3]。由于引入了循环,RNN具备有限短期记忆的优势。
然而,第一代RNN网络并没有引起世人瞩目。这是因为RNN在利用反向传播调参过程中产生了严重的梯度消失问题。随后,上世纪90年代后期出现了重大突破,如LSTM(Long Short-Term Memory,长短期记忆网络[4])等模型的提出,让新一代的RNN获得蓬勃发展。
RNN在自然语言处理领域中最先被用起来的。例如,当前深度学习大家之一Yoshua Bengio,2003年就把RNN用于优化传统的N元统计模型(N-gram Model)[5],提出了关于单词的分布式特征表示(distributed representation for words),较好地解决了传统语言处理模型的“维度咒诅(Curse of Dimensionality)”问题。
到后来,RNN的“作用越”越来越大,并不限于自然语言处理,它还在“机器翻译”、“语音识别(如谷歌的语音搜索,苹果的Siri)应用”、“个性化推荐”等众多领域大放光彩,成为深度学习的三大模型之一。其他两个分别模型分别是卷积神经网络(CNN)和深度信念网络(DBN)。
14.3 Elman递归神经网络
循环神经网络之所以称之为“循环”,就是因为它的网络表现形式有循环结构,从而使得过去输出的信息作为记忆而被保留下来,并可应用于当前输出的计算中。也就是说,RNN的同一隐层之间的节点是有连接的。
图14-3是传统的Elman RNN网络模型的展开结构图。无论是循环图,还是展开图,都有其作用。循环图(左图)比较简洁,而展开图则能表明其中的计算流程。
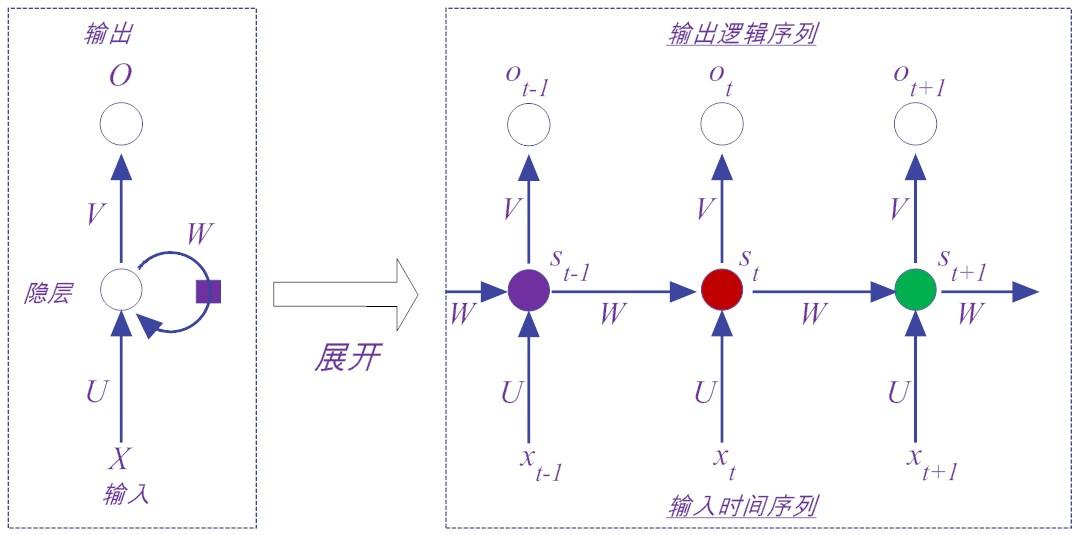
观察图14-3可以看到,Elman RNN网络模型除了 X 向量表示输入层的值, O 向量表示输出层的值之外,一共就有三类参数值,分别是 U 、 V 和 W 。假设输入层神经元个数为 n 个,隐层的神经元个数为 m 个,输出层的神经元个数为 r ,那么 U 是输入层到隐藏层的权重矩阵,大小为( n × m )维; V 是隐层到输出层的权重矩阵,大小为( m × r )维。前面这两个参数矩阵和前馈神经网络的完全一样。
那么, W 又是什么呢?通过前面的介绍我们知道,RNN中隐层 s ( t )的值,不仅仅取决于当前输入 x ,还取决于上一次隐层的值 s ( t-1 )。如此一来, W 表示的就是隐藏层上一次输出值而作为本次输入的权重矩阵,大小为( m × m )维。
从图14-3中可以看到,在理论上,这个模型可以扩展到无限维,也就是可以支撑无限的时间序列,但实际并非如此,就如同人脑的记忆力是有限的一样。下面我们对Elman RNN网络的结构和符号进行形式化定义。我们先用一个函数 f ( t )表示经过 t 步展开后的循环,如公式(14-1)所示。
\begin{array}{l} {s^{(t)}} = {f^{(t)}}({{\bf{x}}^{(t)}},{{\bf{x}}^{(t - 1)}},{{\bf{x}}^{(t - 2)}},...,{{\bf{x}}^{(0)}},{{\bf{x}}^{(1)}}) \\ {\rm{ = }}\left\{ \begin{array}{l} 0,{\rm{ }}t = - 1 \\ \sigma ({s^{(t - 1)}},{{\bf{x}}^{(t)}};\theta ){\rm{ }}t \ge 0{\rm{ }} \\ \end{array} \right. \\ \end{array}\tag{14-1}
函数 f^{(t)} 将过去的所有序列 X = ({{\bf{x}}^{(t)}},{{\bf{x}}^{(t - 1)}},{{\bf{x}}^{(t - 2)}},...,{{\bf{x}}^{(0)}},{{\bf{x}}^{(1)}}) 作为输入,从而生成当前的状态,其中 θ 表示激活函数 σ 中所有的参数集合。 X^{(t)} 表示序列中的第 t 时刻或第 t 时间步的输入数据,它通常也是一个向量; s^{(t)} 向量,表示隐层的值,如图14-4所示。
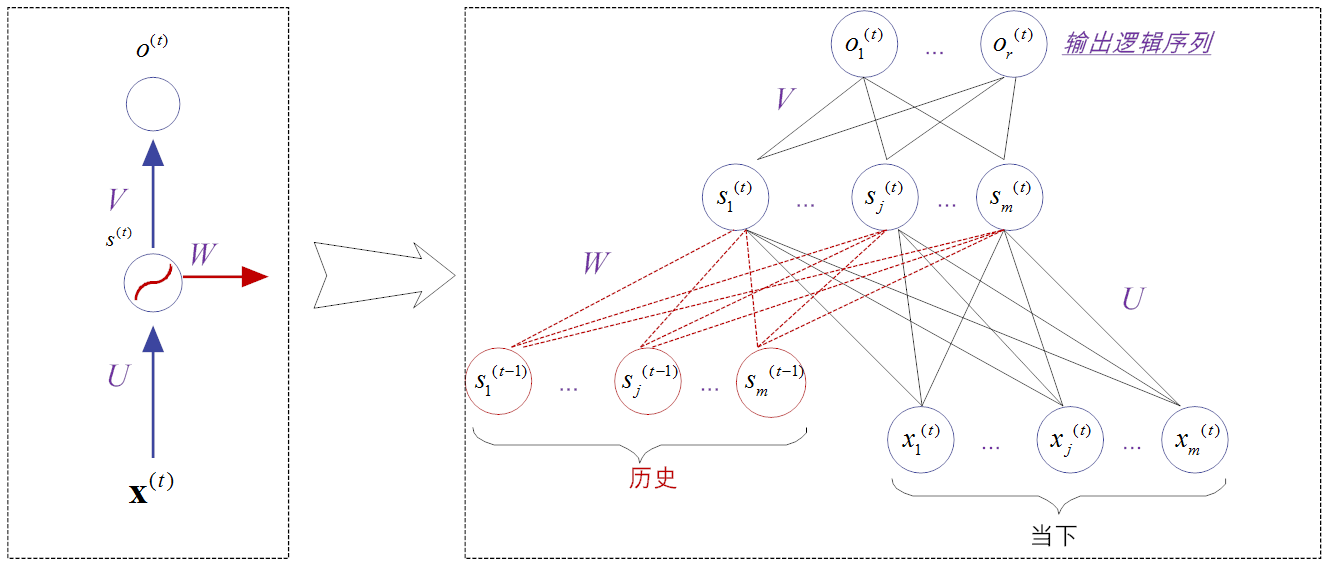
从图14-4可以看到,隐层是RNN模型最核心的模型,也是处理“记忆”信息的地方。事实上,不同类型的递归网络的设计,其差别都体现在隐层设计的不同上。
在公式(14-1)中,激活函数 σ 是一个平滑的、非线性的有界函数,它可以是前些章节提到的Sigmoid、Tanh或ReLU等。一般来讲,我们还需要设定一个特殊的初始隐藏带有 s ( - 1),表明初始的“记忆状态”,通常都会将其置为零。
不论是从图14-4,还是从公式(14-1),都可以看到,第 t 时间的记忆信息是由前( t -1)个时间步累计而成的结果 s^{(t-1)} 和当前的输出 x^{(t)}
共同决定的。这些信息保存在隐层中,不断向后传递,跨越多个时间步,共同影响每个输入新信息的处理结果[6]。
13.4 循环神经网络的生物学机理
RNN利用环路(即上一层的输出)来当做本层的部分输入,其机制与动物大脑的工作机制非常类似。人们常说,“书读百遍,其义自见”。
书为什么要读百遍呢?这里的“百遍”自然是虚词,表示很多遍,它表示一种强化记忆的动作。
那什么叫强化呢?就是在前期留下记忆的基础之上再和本次重新输入的“读书”,叠加起来,逐渐沉淀下来,最终成为我们的经验知识。
众所周知,大脑中包含数亿万神经元,这些神经元又通过更高数量级的突触(Synapse)相互连接。尽管揭示大脑的全部奥秘,“路漫漫其修远兮”,但曙光已乍现。
2015年,美国贝勒医学院(Baylor College of Medicine)的研究者们在著名学术期刊《Science》撰文表示,在大脑皮层中,局部回路的基本连接,可以通过一系列的互联规则所捕获(如图14-5),而且这些规则在大脑皮层中处于不断循环之中[7]。
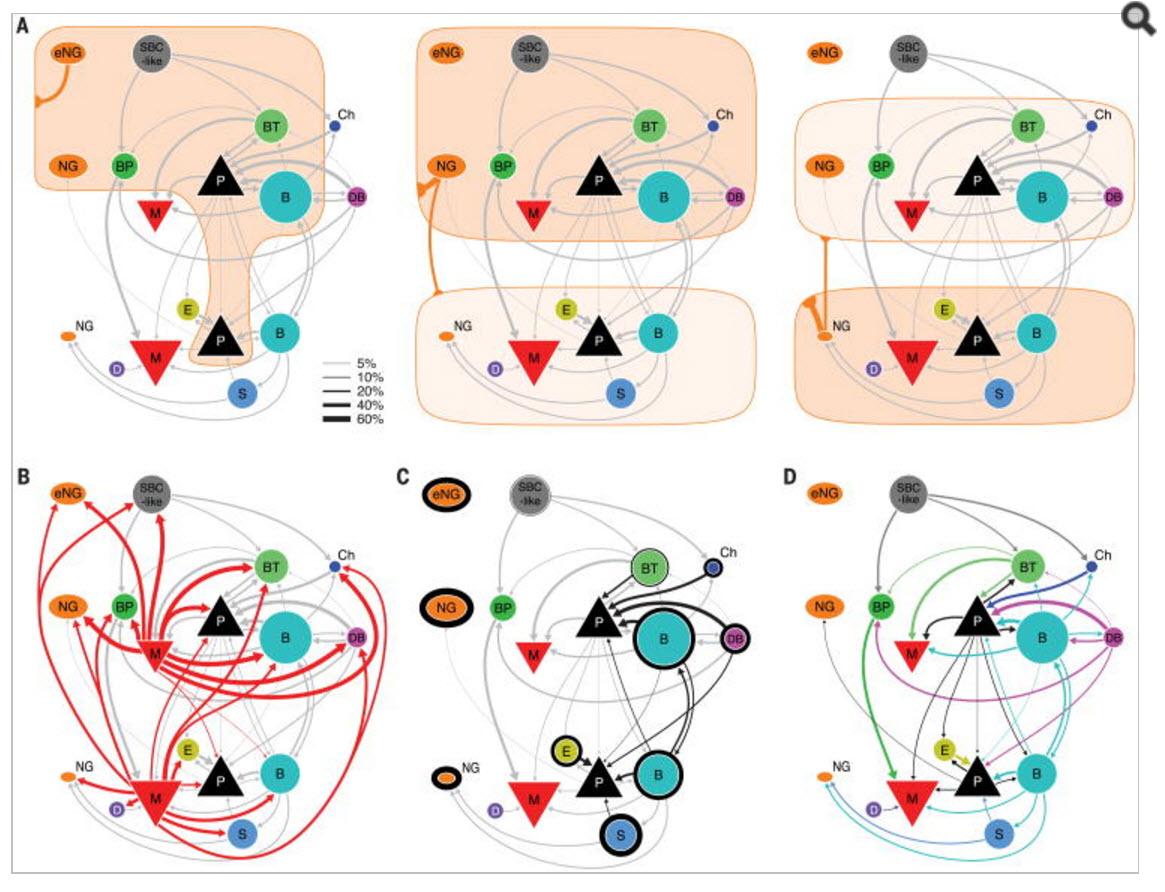
RNN通过使用带有自反馈的神经元,能够处理理论上任意长度的(存在时间关联性的)序列数据。相比于传统的前馈神经网络,它更符合生物神经元的连接方式,也就是说,如果以模仿大脑来作为终极目标的话,它更有前途。这在某种程度上也说明了近几年RNN研究异常火爆的原因。
14.5 循环神经网络的训练
RNN的结构确定下来之后,接下来的核心工作就是训练RNN了。训练RNN的算法叫做时间反向传播(BackPropagation Through Time,简称BPTT)。看到BP这两个字母,就知道它和传统的反向传播算法BP有类似之处,它们的核心任务都是利用反向传播调参,从而使得损失函数最小化。
BPTT算法包括三个步骤,分别简要介绍如下。
(1)问题建模
最小化损失函数的前提是,先确定下来损失函数的形式。而损失函数就是衡量预期输出和实际输出的差异度函数。作为教师信号,预期输出可视为常量,很早就待在那里。因此,问题建模的首要任务就是,确定隐层和输出层的输出函数分别是什么?
假设隐层用的激活函数是sigmoid(当然也可以是其他激活函数,表达形式稍有变化而已),那么在任意第 t 时间步,隐层的输出 s^{(t)} 可表示为公式(14-2)。
{s^{(t)}} = {{\mathop{\rm sigmoid}\nolimits} ^{}}({U^T} \times {{\bf{x}}^{(t)}} + {W^T} \times {s^{(t - 1)}} + b)\tag{14-2}
在第 t 时间步的输出层 o^{(t)} 可表示为公式(14-3):
{o^{(t)}} = {V^T} \times {s^{(t)}} + c \tag{14-3}
这里 b 和 c 是偏置参数向量。与输入层和隐层不同的是,输出层的设计更加灵活多变,它并不要求每个时间步都必须有输出。比如说,在面向文本分析的情感分类案例中,输入可以是一系列的单词,但输出只是整个句子的情感,它和单词之间并不是一一对应的关系,它只需给出整体的判定分类就可。
对于分类模型,通常输出层在最后还要利用Softmax激活函数做归一化处理(该函数已在前面的文章中做了介绍,不熟悉的读者可 前往查阅 ),该函数将一个 m 维的向量压缩为一个 m 维的实数向量,而且这些实数向量的元素都介于(0, 1)之间,实际上就是一个概率向量。经过softmax函数处理后,最终“修饰”后的输出 y^{(t)} 可用公式(14-4)表示。
{y^{(t)}} = {\rm{softmax(}}{{\rm{o}}^{{\rm{(t)}}}}{\rm{) = softmax}}({V^T} \times {s^{(t)}} + c)\tag{14-4}
(2)优化目标函数
基于前面公式(14-1)至公式(14-4)反映出的模型,接下来就是构建损失函数,然后设法求得损失函数的最小值,这就形成了我们所需优化的目标函数 J ( θ) 。这里为了方便计算,我们使用了负对数似然函数(即交叉熵)。
\begin{array}{l} \min J(\theta ) = \sum\limits_{t = 1}^T {loss(} \mathop {{y^{(t)}}}\limits^ \wedge ,{y^{(t)}}) \\ = \sum\limits_{t = 1}^T {\left( { - \left[ {\sum\limits_{j = 1}^m {{y^{(t)}}(j) \cdot \log (\mathop {{y^{(t)}}}\limits^ \wedge (j) + (1 - {y^{(t)}}(j)) \cdot \log (1 - \mathop {{y^{(t)}}}\limits^ \wedge )} } \right]} \right)} \\ \end{array}\tag{14-5}
其中, y^{(t)}(j) 表示为输出 y (t)的第j个元素。参数 θ 表示激活函数 σ 中的所有参数集合[U, V , W; b , c]。
(3)参数求解
和传统BP反向传播算法一样,BPTT算法的核心也是求解参数的导数。所不同的是,BPTT算法中的参数有5类,如公式(14-6)所示。
\left[ {\frac{{\partial J(\theta )}}{{\partial V}},\frac{{\partial J(\theta )}}{{\partial c}},\frac{{\partial J(\theta )}}{{\partial W}},\frac{{\partial J(\theta )}}{{\partial U}},\frac{{\partial J(\theta )}}{{\partial b}}} \right]\tag{14-6}
在确定目标函数之后,我们就以利用随机梯度下降等优化策略,来指导网络参数的更新。限于篇幅,本文省略了公式(14-6)的偏导数求解推导过程,感兴趣的读者,可以参考黄安埠先生的著作[6]。
由于RNN中采用的激活函数是sigmoid,其导数值域锁定在[0,1/4]范围之内。故此,每一层反向传播过程,梯度都会以前一层1/4的速度递减。可以想象,随着传递时间步数的不断增加,梯度会呈现指数级递减趋势,直至梯度消失(vanishing gradient),如图14-6所示。
假设当前时刻为 t ,那么在( t -3)时刻,梯度将递减至(1/4)^3=1/64,以此类推。
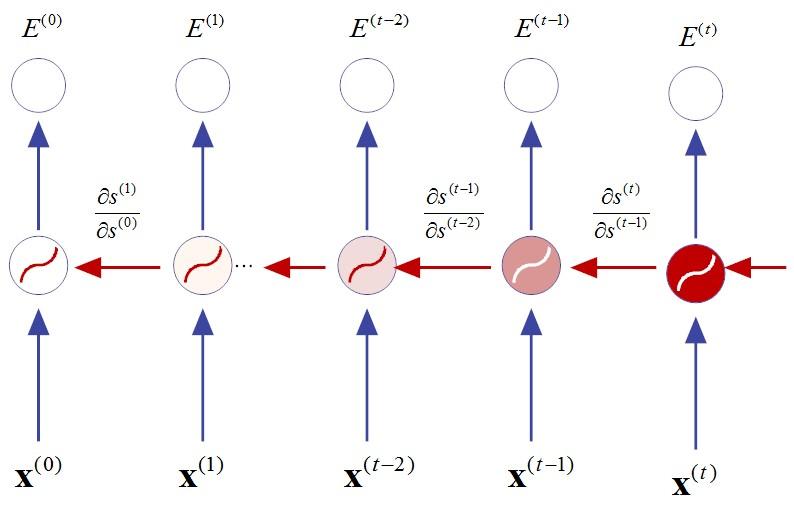
一旦梯度消失(或梯度趋近于0),参数调整就没有了方向感,从而BPTT的最优解也就无从获得,因此RNN的应用受到了局限。
14.6 小结与思考
在本章,我们学习了循环神经网络(RNN)。它最大的特点莫过于,网络的输出结果不仅和当前的输入相关,还和过往的输出相关。由于利用了历史信息,当任务涉及到与时序或与上下文相关时(如语音识别、自然语言处理等),RNN就要比其他人工神经网络(如CNN)的性能要好得多。
但需要读者注意如下两点:(1)RNN中的“深度”,不同于传统的深度神经网络,它主要是指时间和空间(如网络中的隐层个数)特性上的深度。
(2)通过对第十二章的学习,我们知道传统CNN(卷积神经网络)的主要特点是“局部连接”、“权值共享”和“局部平移不变性”,其中“权值共享”意味着“计算共享”,它节省了大量计算开销。而RNN则不同,它是随着“时间”深度的加深,通过对参数实施“平流移植”来实现“计算共享”的。
通过上面的学习,请你思考如下问题:
- 梯度弥散问题在一定程度上阻碍了RNN的进一步发展,你可以想到什么策略来抑制这个问题吗?(提示:初始化策略)
- 除了梯度弥散问题之外,RNN还存在什么问题呢?又是如何解决的呢?
提示:序列中时间特性的依赖关系,可能也会引起长期依赖问题,也就是记忆能力受限。1997年,RNN引入基于LSTM的架构后,性能取得了很大的突破。
LSTM正是我们下一讲的主题,请你关注。
参考文献
[1] Hopfield J J. Neural networks and physical systems with emergent collective computational abilities [J]. Proceedings of the National Academy of Sciences of the United States of America, 1982, 79(8):2554.
[2] Jordan, M. (1986). Serial order: A parallel distributed processing approach. Institute for Cognitive Science Report 8604. University of California, San Diego.
[3] Elman J L. Finding structure in time[J]. Cognitive Science, 1990, 14(2):179-211.
[4] Sepp Hochreiter; Jürgen Schmidhuber (1997). "Long short-term memory". Neural Computation. 9 (8): 1735–1780. PMID 9377276. doi:10.1162/neco.1997.9.8.1735.
[5] Bengio Y, Vincent P, Janvin C. A neural probabilistic language model[J]. Journal of Machine Learning Research, 2003, 3(6):1137-1155.
[6] 黄安埠. 深入浅出深度学习.中国工信出版社.2017.6
[7] Jiang X, Shen S, Cadwell C R, et al. Principles of connectivity among morphologically defined cell types in adult neocortex.[J]. Science, 2015, 350(6264):aac9462.
本文部分节选自《 深度学习之美:AI时代的数据处理与最佳实践 》(张玉宏著,电子工业出版社,2018年7月出版)。更多理论推导及实战环节,请参阅该书。
(连载待续)
如果觉得文章对你有点用,请帮忙点个赞,你的点赞,我更新的动力:)


