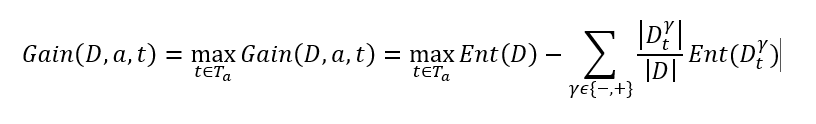if __name__ == '__main__':
dataSet, labels = createDataSet()
tree=createTree(dataSet, labels)
print(tree)
最后打印的结果如下所示:
{'序号': {'>7.5': '女', '<=7.5': {'头发': {'短': {'声音': {'细': '女', '粗': '男'}}, '长': {'声音': {'细': '女', '粗': '男'}}}}}}
全文到此结束。如果觉得对您有用,请帮忙点个赞,谢谢。如果有不对之处,还请指出,谢谢。
声明,决策树理论讲解部分主要参考自周志华的《机器学习》一书。另外,参考资料也一一列举如下,如有异议,请直接联系笔者修改或删除。
参考资料:
[1]: 《机器学习》周志华
本文实例讲述了决策树剪枝算法的python实现方法。分享给大家供大家参考,具体如下:决策树是一种依托决策而建立起来的一种树。在机器学习中,决策树是一种预测模型,代表的是一种对象属性与对象值之间的一种映射关系,每一个节点代表某个对象,树中的每一个分叉路径代表某个可能的属性值,而每一个叶子节点则对应从根节点到该叶子节点所经历的路径所表示的对象的值。决策树仅有单一输出,如果有多个输出,可以分别建立独立的...
决策树是一种用于分类和回归任务的非参数监督学习算法。它是一种分层树形结构,由根节点、分支、内部节点和叶节点组成。从上图中可以看出,决策树从根节点开始,根节点没有任何传入分支。然后,根节点的传出分支为内部节点(也称为决策节点)提供信息。两种节点都基于可用功能执行评估以形成同类子集,这些子集由叶节点或终端节点表示。叶节点表示数据集内所有可能的结果。决策树的类型Hunt 算法于 20 世纪 60 年代提...
为什么要进行剪枝?当我们的数据集样本量很大、每个特征的取值很多时,生成决策树的代价就会很大。不仅如此,虽然一个完整的决策树对训练数据的预测非常准,但这会造成对训练数据的过拟合,造成模型的泛化性能(预测除训练集意外数据的能力)降低。因此,本节我们将引入剪枝的概念。预剪枝其实就是在生成决策树的过程中边生成决策树边剪枝。预剪枝在构建决策树的过程中,计算以下两个精确度:1、如果不划分样本集合此时模型在验证集上的精确度;2、如果划分样本集合此时模型在验证集上的精确度。如果划分后的精确度更高,说明此时。
1.首先,是否要按照“脐部”划分。在划分前,只有一个根节点,也是叶子节点,标记为“好瓜”。通过测试集验证,只有{4,5,8}3个样本可以正确分类,精度为3/7=42.9%。当按照脐部划分后,再进行验证,发现{4,5,8,11,12}被正确分类,精度为5/7=71.4%。精度提高,所以按照“脐部”进行划分。2.当按照脐部进行划分后,会对结点 (2) 进行划分,再次使用信息增益挑选出值最大的那个特征,信息增益值最大的那个特征是“色泽”,则使用“色泽”划分后决策树。
预剪枝在决策树生成过程中对每个节点先进行估计,如果划分能带来准确率上升则划分,否者不划分节点;后剪枝则是先使用训练集生成一棵决策树,再使用测试集对其节点进行评估,若将子树替换为叶子结点能带来准确率的提升则替换。
– 第一步:将连续属性 a 在样本集 D 上出现 n 个不同的取值从小到大排列,记为 a 1 , a 2 , ..., an。基于划分点t,可将D分为子集Dt +和Dt-,其中Dt-包含那些在属性a上取值不大于t的样本,Dt+包含那些在属性 a上取值大于t的样本。考虑包含n-1个元素的候选划分点集合即把区间[a i , a i-1) 的
1 剪枝概述
剪枝是搜索常用的优化手段,常常能把指数级的复杂度,优化到近似多项式的复杂度。
剪枝是一个比喻:把不会产生答案的,或不必要的枝条“剪掉”。剪枝的关键在于剪枝的判断:什么枝该剪、在什么地方减。
BFS的剪枝通常是判重,如果搜索到某一层时,出现重复的状态,就剪枝。例如经典的八数码问题,核心问题就是去重,把曾经搜过的八数码的组合剪去。
DFS的剪枝技术较多,有可行性剪枝、最优性剪枝、搜索顺序剪枝、排除等效冗余、记忆化搜索等等。
可行性剪枝:对当前状态进行检