时间序列（三）：python建立ARMA和ARIMA模型

4 年前 · 来自专栏啥子数据

Big冯

科学与艺术在山脚下分手，在山顶会合。

1. ARMA

ARMA与上期我们的AR模型有着相同的特征方程，该方程所有解的倒数称为该模型的特征根，如果所有的特征根的模都小于1，则该ARMA模型是平稳的。 ARMA模型的应用对象应该为平稳序列！ 我们下面的步骤都是建立在假设原序列平稳的条件下的。

2. 单位根检验（Dickey-Fuller test）

from statsmodels.tsa.stattools import adfuller
temp = np.array(data)
t = adfuller(temp)  # ADF检验
output=pd.DataFrame(index=['Test Statistic Value', "p-value", "Lags Used", "Number of Observations Used","Critical Value(1%)","Critical Value(5%)","Critical Value(10%)"],columns=['value'])
output['value']['Test Statistic Value'] = t[0]
output['value']['p-value'] = t[1]
output['value']['Lags Used'] = t[2]
output['value']['Number of Observations Used'] = t[3]
output['value']['Critical Value(1%)'] = t[4]['1%']
output['value']['Critical Value(5%)'] = t[4]['5%']
output['value']['Critical Value(10%)'] = t[4]['10%']
output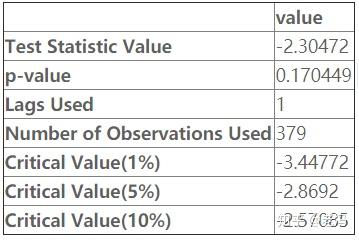

3. ARMA(p,q)模型阶次

1) 我们通过观察PACF和ACF截尾，分别判断p、q的值。

# ACF and PACF 
from statsmodels.tsa.stattools import acf, pacf，plot_acf, plot_pacf
lag_acf = acf(data, nlags=20)
lag_pacf = pacf(data, nlags=20, method='ols')
fig, axes = plt.subplots(1,2, figsize=(20,5))
plot_acf(ts, lags=100, ax=axes[0])
plot_pacf(ts, lags=100, ax=axes[1])
plt.show()

2) 信息准则定阶

我们常用的是AIC准则，AIC鼓励数据拟合的优良性但是尽量避免出现过度拟合(Overfitting)的情况。所以优先考虑的模型应是AIC值最小的那一个模型。

# 为了控制计算量，我们限制AR最大阶不超过6，MA最大阶不超过4。
sm.tsa.arma_order_select_ic(data,max_ar=6,max_ma=4,ic='aic')['aic_min_order']  # AIC

两种定阶的方法结果不一定一致，一般采用第一种，也可通过模型的效果进行取舍。

4. ARMA建模及预测

定阶(order)之后就能构建ARMA模型了。

# 模型阶次(3,3)来建立ARMA模型，最后10个数据用于预测。
from statsmodels.tsa import ARMA
order = (3,3)
train = data[:-10]
test = data[-10:]
tempModel = ARMA(train,order).fit()

拟合优度AdjR^2

delta = tempModel.fittedvalues - train # 残差
score = 1 - delta.var()/train.var()
# 它的值在0-1之间，越接近1，拟合效果越好

预测最后10个数据并与实际值比较

predicts = tempModel.predict(371, 380, dynamic=True)
print len(predicts)
comp = pd.DataFrame()
comp['original'] = test
comp['predict'] = predicts