python小结1：数字型；案例-计算器

薯条蘸酱

本篇主要讲解：int型的不同进制的表达方式；float型的精度问题；考虑精度问题的计算器的编写；以及扩展数字类型Decimal和Fraction 。

一、类型

python的数字型类型包括：

基础类型

整数 int
布尔类型 bool-->是int类的子类。issubclass(bool,int)返回True
浮点数 float
复数 complex

扩展数字类型 （需要导入相应的标准库，不支持复数）

表示分数的fractions.Fraction
防止精度问题的浮点数decimal.Decimal

Python基础类型完全支持混合运算：当运算对象有不同数值类型时，"较窄"类型的操作数会拓宽到另一个操作数的类型，其中整数比浮点数窄，浮点数比复数窄。

而扩展数字类型需要将计算的值转为为Fraction或Decimal再进行计算，如果与浮点数进行混合计算会报错。

二、运算

所有数字类型（复数除外）都支持下列运算。

运算符	描述	实例	方法
+	x加y		__add__
-	x减去y		__sub__
*	x乘以y		__mul__
/	x除以y		__truediv__
%	取模：返回除法的余数	30 % 10 输出结果 0	__mod__
**	x 的 y 次幂	a**b 为10的20次方，输出结果 100000000000000000000	__pow__
//	取整除：返回商的整数部分（向下取整）	>>> 9//2 4>>> -9//2-5	__floordiv__
+x	x 不变		__pos__
-x	x 取反		__neg__
abs(x)	x的绝对值或复数的模		__pow__
int(x)	将x转化为整数		__int__
float(x)	将x转化为浮点数		__float__
complex(a,b)	创建一个实部为a，虚部为b的复数。		__complex__
c.conjugate()	返回复数c的共轭复数
divmod(x,y)	返回(x//y,x%y)		__divmod__
pow(x,y	x 的 y 次幂		__pow__

Python 将 pow(0, 0) 和 0 ** 0 定义为 1，这是编程语言的普遍做法。

注意：

①如果想要在自己创建的类中适用上面的算数运算符，需要在类中添加相应的方法。

例如：创建一个苹果类，属性是重量，我们可以设置def __add__(self,other):，这样就可以使用“+”对对象进行操作。如果不进行设置，就只能获得对象的属性（数字型）后再进行相加。

class Apple:
    def __init__(self,type_apple,weight):
        self.type_apple = type_apple
        self.weight = weight
    def __add__(self,other):
        return self.weight + other.weight
    def __mul__(self,other):
        return self.




    
weight * other.weight        
    def __pow__(self,other):
        return self.weight ** other.weight    
    def __str__(self):
        return f"我是一个{self.type_apple}，重{self.weight}克"
a = Apple("青苹果",300)
b = Apple("红苹果",20)
print(a)
print(b)
print(a+b)
print(a*b)
print(a**b)

②//取整除：返回商的整数部分（向下取整）

所以，有人喜欢用int(a/b)去获得商，在a、b符号相反的时候是错误的。

int(-9/2)
Out[11]: -4
-9//2
Out[12]: -5

二、整数

2.1整型的表现形式

2 进制：以'0b'开头。例如：'0b1100100' 表示10进制的100
8 进制：以'0o'开头。例如：'0o33'表示10进制的27
10进制：正常显示
16进制：以'0x'开头。例如：'0x1b'表示10进制的27

各进间数字进行转换（内置函数）：

bin（i）：将i转换为2进制，以“0b”开头。

oct（i）：将i转换为8进制，以“0o”开头。

int（i）：将i转换为10进制，正常显示。

hex（i）：将i转换为16进制，以“0x”开头。

这些函数，只能用于对整数进行转化。

a = 0b1100100 #赋值为100

print(bin(100)) #得到'0b1100100'

进制判断

一般情况下是不需要用十进制以外的运算。 但是如果遇到了，也应该知道是什么意思。

很简单， 如果一个数字以0开头，那么首先考虑是采用了十进制以外的表现形式。

因为 a = 0100 会出现报错。如果不报错，那就是其他表现形式。

SyntaxError: leading zeros in decimal integer literals are not permitted; use an 0o prefix for octal integers

2.2整数类型的按位运算

按位运算只对整数有意义。

注释：

负的移位数是非法的，会导致引发 ValueError。
左移 n 位等价于乘以 pow(2, n) 。
右移 n 位等价于除以 pow(2, n) ，作向下取整除法。

2.3整数的混合运算

当运算对象有不同数值类型时，"较窄"类型的操作数会拓宽到另一个操作数的类型，其中整数比浮点数窄，浮点数比复数窄。

所以一般情况下，整数经过一系列计算之后，很可能会得到一个浮点数。

有几种情况需要注意。

1）函数标注了参数的类型。

def Point(num: int):
    print(num)
Point(3)
Point(3.0)

Point()标注了传入的num应该是整数int型。 但是我们发现，实际上并不会报错。 是否报错跟函数的具体语句相关。

但是这不代表你不用关心数字的具体类型。比如字符串的insert()方法注明了传入的参数应该是整数，传入3.0这种数字也是报错的。如果你不知道函数内部到底是怎么运作的，还是按照要求传递参数。

我们输入a.insert(1.0, 6)，就会提示：integer argument expected, got float

所以在通过复杂运算之后，如果函数指定传入int。尽可能转为为整数型后再作为参数使用。

2）在向其他系统发送请求的时候。

比如如果你需要进行量化交易。交易所规定合约数量必须是整数。

设想一种情况： 一般情况下，你用a = 3作为合约数量发送请求，一直没有报错，就不甚在意。

但是某一天，你的程序触发了加仓命令。合约数量增加现有持仓的一半。

持仓：b = 100

默认合约数：a = 3

你出发的请求就是 3+100/2，得到的是53.0。虽然53和53.0好像没什么区别。但是这个时候，会提示错误。如果你的请求加了循环，还会在这个步骤一直卡住。大概的情况可能就是这样。

3）整数运算之后的情况变化列举

a = 1 + 3    #4
a = 1 + 3.0  #4.0
a = 6 / 2    #4.0
a = 6 /2.0   #4.0
a = 6.0 / 2.0   #4.0
a = 1 * 3    #3
a = 1.0 * 3  #3.0

除了简单的整数之间的加减乘，其他情况计算后都可能得到小数。

4）取整的方式

①去尾： int()

int(3.1415)   # 3
int(-4.9)     # -4

②四舍五入 round()

round(-3.5)  # -4
round(3.5)   # 4
round(-3.8)  # -4
round(3.8)   # 4
round(-




    
3.2)  # -3
round(3.2)   # 3

③向下取整 math.floor()

math.floor(-3.8)   # -4
math.floor(3.8)    # 3
math.floor(-3.14)  # -4
math.floor(3.14)   # 3

这里用到了math内置模块。

④向上取整 math.ceil()

很多人认为int()就是向下取整。 但是实际上，int(-4.9) 得到的是-4。

import math
math.ceil(3.14)  #4
math.ceil(-3.14) # -3
math.ceil(3.8)  #4
math.ceil(-3.8) # -3

这里用到了math内置模块。

5）取商

这里再回到上面提到的整除取商。

int(11/2) 大多数情况是没啥影响的，实际上，我们经常处理的就是正数，但是保不齐就会出现负数。

取商的结果是向下取整。被除数为正，余数就是正。被除数是负，余数就是负。

实际上，一般都是结合商和余数一起看的。

三、浮点数

浮点型由整数部分与小数部分组成

3.1.科学计数法

浮点型也可以使用科学计数法表示

a = 3.14159e3
print(a)
-->3141.59

这种输入是能识别的。也可以用科学计数法进行打印输出。%e

print("%e"%a)
-->3.141590e+03

3.2.计算精度问题

我们知道浮点数在进行计算的时候，会存在精度缺失的问题。大多数的十进制小数都不能精确地表示为二进制小数。这导致在大多数情况下，你输入的十进制浮点数都只能近似地以二进制浮点数形式储存在计算机中。

例如：

0.1 + 0.2
--> 0.30000000000000004
1.111111111111111111111111111111 -0.000000000000000000000000000001
1.1111111111111112
相减结果反而变大了。

3.3.如何处理精度

①倍数法

0.7+0.1

结果：0.7999999999999999

改成：

(7+1)/10

结果：0.8

缺点：前期准备麻烦，也容易因为操作失误而出错。

②四舍五入

比如常见的金额，我们保留的是小数点后两位，浮点数计算的偏差一般都很小。

例如：在计算金额总计的时候，如果计算次数太多，你可能认为偏差会很大。但是实际上呢？

比如金额为71.13。我们逐步累加一百万次。

a = 0
for i in range(1000000):
    a = 71.13 + a

结果：71130000.00083488。

偏差还是在小数点2位之后。这个时候再使用round(数字,精度)就可以较好的解决问题。

0.70+0.10==>0.7999999999999999

round(0.70+0.10,2) ==>0.8

缺点： 如果小数是被除数，可能浮点数存储上的较小偏差也会导致结果上的较大误差。

③Decimal 类型

Decimal的意思是”十进制“。

Decimal是decimal模块里面规定的类。

decimal 模块旨在支持“无偏差，精确无舍入的十进制算术（有时称为定点数算术）和有舍入的浮点数算术”。

相关文档见：

用法： 将数字用 字符串 的形式输入。

from decimal import Decimal

Decimal("0.7")+Decimal("0.1") 可以计算得到：Decimal('0.8')

Decimal(0.7)+Decimal(0.1) 可以计算得到：Decimal('0.7999999999999999611421941381')

所以输入参数的时候用字符串的形式。

如果需要得到结果，因为设置了__ str _ 和__int__ 。所以直接print()或者str()

Decimal("0.7")+Decimal("0.1") float(a) Out[1]: 0.8 int(a) Out[2]: 0 print(a) Out[3]:0.8

案例：考虑数精度的计算器

比如用python做一个计算器。

随便网上拿一个代码。

import tkinter # 获取一个窗口 window = tkinter.Tk() # 设置标题 window.title('计算器') # 设置窗口大小 window.geometry('200x200') # 输入方法 def add(n): # 获取到n1文本框的值 n1 = inp.get() # 清空文本框 inp.delete(0,len(n1)) # 插入原来的加上新输入参数n inp.insert(0,n1+str(n)) # 执行计算方法 def calc(): n1 = inp.get() inp.delete(0,len(n1)) # 把文本框的字符串用eval当代码执行一次，再插入到文本框 inp.insert(0,str(eval(n1))) # 清空文本框 def clear(): n1 = inp.get() inp.delete(0,len(n1)) # 删除最后一个字符 def back(): n1 = inp.get() inp.delete(len(n1)-1,len(n1)) # 计算绝对值 def ab(): n1 = inp.get() inp.delete(0,len(n1)) inp.insert(0,str(eval(n1)*-1)) # 设置一个文本框 inp = tkinter.Entry(window, width=25) # 在第0行，第0个，合并5列 inp.grid(row=0,column=0,columnspan=5) # 用for循环创建 123 456 789 9个按钮 for i in range(0,3): for j in range(1,4): n = j+i*3 btn=tkinter.Button(window, text=str(j+i*3),width=5, command=lambda n=n:add(n)) btn.grid(row=i+2,column=j-1) # 删除按钮(窗口,宽度，文本，执行命令).grid(1行,0列) tkinter.Button(window,width=5, text="C", command=clear).grid(row=1,column=0) tkinter.Button(window,width=5, text="←", command=back).grid(row=1,column=1) tkinter.Button(window,width=5, text="+/-", command=ab).grid(row=1,column=2) # 删除按钮(窗口,宽度，文本，背景色，文本颜色，执行命令并传入参数).grid(1行,4列) tkinter.Button(window,width=5, text="+",bg="#f70",fg="#fff",command=lambda:add("+")).grid(row=1,column=4) tkinter.Button(window,width=5, text="-", bg="#f70",fg="#fff",command=lambda:add("-")).grid(row=2,column=4) tkinter.Button(window,width=5, text="×",bg="#f70",fg="#fff",command=lambda:add("*")).grid(row=3,column=4) tkinter.Button(window,width=5, text="÷",bg="#f70",fg="#fff",command=lambda:add("/")).grid(row=4,column=4) tkinter.Button(window,width=12,text="0", command=lambda:add("0")).grid(row=5,column=0,columnspan=2) tkinter.Button(window,width=5,text="=", bg="#f70",fg="#fff",command=calc).grid(row=5,column=4) tkinter.Button(window,width=5, text=".", command=lambda:add(".")).grid(row=5,column=2) # 进入消息循环 window.mainloop()

但是我们计算0.7+0.1，得到的结果是：

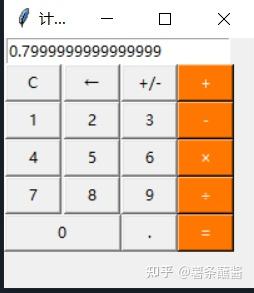
这种情况的计算器在生活中是没有太大意义的。

上面的计算器是按照eval("公式")进行的。这里不考虑eval()安全性的问题。

eval()虽然能够很好的识别"1.235*6.0-0.1"这种表达式，但是运算上还是采用的浮点数的运算方式。会存在精度问题。

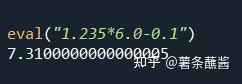
Decimal可以很好的计算十进制的浮点数，但是表达上很麻烦。比如：

eval("1.235*6.0-0.1")

结果是7.3100000000000005

Decimal("1.235*6.0-0.1")

报错

Decimal("1.235")*Decimal("6.0")-Decimal("0.1")

结果是Decimal('7.3100')

虽然我们一般计算不会在意那么一点点的偏差，但是这里，我们要作为计算器使用还是想要”结果“不那么反人类。

【修改步骤1】

建立一个eval_decimal()函数去进行Decimal方式的计算。

def eval_decimal(n): list_math=re.split("([\(\)\+\-\*/])",n) #分割字符串，获得运算符和数字组成的列表。 length = len(list_math) for i in range(length): try: float(list_math[i ]) #判断是否为数字 list_math[i] = "Decimal(\'"+list_math[i]+"\')" #将数字用Decimal对象代替 except ValueError: text_math = "".join(list_math) #拼接成新的字符串 num = eval(text_math) #计算 return str(num)

然后计算器就可以较好的得出结果了。

比如：0.1+0.7

比如："1.235*6.0-0.1"

但是上面仍然有不太理想的地方。

【修改步骤2】

问题1： 用Decimal计算“1/3*3"的时候。

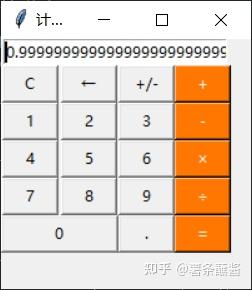
我们直接计算呢？

1/3*3

得到 1.0

这里并不是说浮点数计算更精准，而是因为浮点数中，a = 0.9999999999999999999999赋值的时候，就直接是1.0了。

问题二 ：得到的结果小数结尾部分的0不会自动去掉

方案一： 先将Decimal对象转化为float，然后再转为str。

return str(num)修改为return str(float(num))

结果：已经能去除浮点数末尾多余的0，进行四舍五入。

上面的计算器已经能够较好地用于一般的计算了。

Decimal缺点： 使用上较float麻烦一些，解决了浮点数不能完全表达所有小数的问题。但是因为默认处理28位小数，会存在精度问题。就算你将默认处理精度提高，在遇到无法完全整除的情况，比如“1/3"，仍会有精度问题，这是有限小数表示无限小数都面临的问题。

④分数 Fraction

Fraction是一种存储分数的类。可以输入数字、数字字符串。

相关文档见：

Fraction存储的是分子和分母。比如0，分子就是0，分母是1。

Fraction(1) Out[1]: Fraction(1, 1) Fraction("1") Out[2]: Fraction(1, 1) Fraction(0) Out[3]: Fraction(0, 1) Fraction("0") Out[4]: Fraction(0, 1) Fraction(7/3) Out[5]: Fraction(5254199565265579, 2251799813685248) Fraction("7/3") Out[6]: Fraction(7, 3)

从上面看到。Fraction(7/3)和Fraction("7/3")区别巨大，是因为前者先进行了计算，然后再存为分数。

所以在使用Fraction类的时候，跟Decimal一样，用字符串作为参数。

另外， Fraction会自动约分处理。比如：

Fraction("-24/9") Out[1]: Fraction(-8, 3)

我们计算一下：

\frac{1}{7}+\frac{7}{23}+2

Fraction("1/7")+Fraction("7/23")+Fraction("2") Out[1]:Fraction(394, 161)

得到 \frac{394}{161}

再以上面的计算器为例子。

我们只需要将Decimal改为Fraction，就可以进行分数运算了。

def eval_fraction(n): list_math = re.split("([\(\)\+\-\*/])", n) length = len(list_math) for i in range(length): try: float(list_math[i]) list_math[i] = "Fraction(\'" + list_math[i] + "\')" except ValueError: text_math = "".join(list_math) print(text_math) num = eval(text_math) return str(num)

Fraction优点：除了使用上较float麻烦一些。可以说是完美解决了有理数的计算问题。

需要额外提示的是：Decimal和Fraction都不支持复数。

四、复数complex

复数由实数部分和虚数部分构成，可以用a + bj,或者complex(a,b)表示，复数的实部a和虚部b都是浮点型。虚数部分必须有后缀j或J

4.1.创建

a = 3 + 2j Out[1]: (3+ 2j) b = complex(2, -6) Out[2]: (2-6j)

4.2.属性

real：实部

imag：虚部

int和float型都有这两个属性，比如 3.6.imag为0。因为这种情况我们根本不会去看它们的虚部。

4.3.方法

.conjugate() 返回共轭复数

(3 + 2j).conjugate() Out[1]: (3-2j)

4.4.比较

复数不能进行大小的比较。而相等的判断就是实部和虚部一样。

(3-2j) == (3-2j) 为True。其他情况都为False。

另外，如果使用>或者<判断，会直接报错。

abs(3+4j)求的是复数的模。如果比较模，可以用abs()函数。

五、布尔类

所有标准对象均可用于布尔测试。每个标准对象天生具有布尔True或False值。空对象,值为零的任何数字或者Null对象None的布尔值都是False。在Python3中True=1，False=0，布尔类是int的子类，可以和数字型进行运算。

5/True*(0.5+False) 的结果是2.5

5.1False的情况

bool(对象) 用于测试对象的布尔值。

下列对象的布尔值是False：

None；False；0（整型），0.0（浮点型）；0.0+0.0j（复数）； “”（空字符串）；[]（空列表）；（）（空元组）；{}（空字典）；set()（空集合） 。

注意：

对于容器类型。内部只要有元素，就算作为True。就算元素是空。

a =[""] b ={""} bool(a) Out[1]: True bool(b) Out[2]: True

5.2自建类的布尔值

一般情况下，我们创建的类，都是用” if 类.属性: “的方式进行条件判断。但是如果我们想用”if 32：“这种表达呢？

我们测试一下。

class Test: a = Test() if a: print(True) else: print(False)

结果：True

这里创建了一个既没有属性又没有方法的类。 但是判断时候，仍然认为它是True。

所以我们自建类的布尔值默认就是True。但是这样就失去了对它进行布尔判断的意义。

我们设置__ bool __

class Apple: def __init__(self,type_apple,weight): self.type_apple = type_apple self.weight = weight def __str__(self): return f"我是一个{self.type_apple}，重{self.weight}克" def __bool__(self): if self.weight > 50: return True else: return False a = Apple("青苹果",300) b = Apple("红苹果",20) print(bool(a)) print(bool(b))

结果：True , False

我们设置了__bool__()返回的条件是，苹果的重量超过50为True，否则为False。

这样我们创建的对象就用做判断了。当然这里设置的方式，根据对象的特点而定，也可以设置重量大于0就为True。

六、不可变对象

我们知道int、str、complex是不可变对象。

就比如数字3。拥有属性.real。也就是它的实部。

我们无法修改它的实部。

a = 3 a.real = 6

会报错。AttributeError: attribute 'real' of 'int' objects is not writable

另外，decimal和Fraction也是不可变类型。

6.1增强运算符

因为数字类是不可变类型，所以a = a + b和a += b没什么区别。

a = 1 print(id(a)) a = a + 1 print(id(a)) 2365248203056 2365248203088 a = 1 print(id(a)) a += 1 print(id(a)) 2365248203056 2365248203088

看到数字对象经过=或者+=后的地址都发生了改变。

而针对列表则不一样。

a = [1,2,3] print(id(a)) a = a + [4] print(id(a)) 2365429530880 2365410055808 a = [1,2,3] print(id(a)) a += [4] print(id(a)) 2365429510720 2365429510720

列表在进行+=运算的时候，实际上与.append()方法没什么区别。

在进行a = a + b运算的时候，地址发生了变化。两者在时间复杂度上不一致的。

例如用循环方式创建一个0-999999的列表。

import time a = [] start=time.time() for i in range(1000000): a+=[i] print('+=计算时间为',time.time()-start,'秒')

结果：+=计算时间为 0.18846368789672852 秒

import time a = [] start=time.time() for i in range(1000000): a=a+[i] print('=计算时间为',time.time()-start,'秒')

结果：时间很长......懒得等了。

这里a=a+[i]因为不断增长的列表需要写入新的地址，导致循环运算在后期越来越慢。

+=和=运算，在数字中没什么影响。但是在列表运算中有较大的影响。但是对列表操作，我们也习惯性使用.append()方法。

七、数字判断

我们可能会判断字段串中的内容是否是有效数字。比如：

["\x29", "\x30", b"100", "三", "\059", "\060", "abc", "7.0", "7"]

常用的转化方法：

float(str)

unicodedata.numeric(str) -->需要import unicodedata

先看float(str)

float(str)可以识别全角和半角的数字，以及半角的小数点

float("三") -->错误 float("３．０") #数字和小数点都是全角 -->错误 float("３.０") #数字全角，小数点半角 -->3.0 float("3.0") #全半角 -->3.0

unicodedata.numeric(str)呢？

unicodedata.numeric(str)的输入项只能是一个字符！

unicodedata.numeric("三") -->3.0 unicodedata.numeric("三零") -->错误

所以unicodedata.numeric(str)的限制很大。我们一般也不用。

常用的判断方法：

①str.isdigit()

str.isdigit() 判断文本中是否只有数字（全角或者半角或者byte），如果有小数点，就返回False。

"3".isdigit() -->True "-3".isdigit() -->False b"3".isdigit() -->True b"3.0".isdigit() -->False "030".isdigit() -->True "０３０".isdigit() -->True "3.0".isdigit() -->False "三".isdigit() -->False "叁".isdigit() -->False

所以，str.isdigit()可以用于对输入项要求是自然数的内容的判断。

②str.isdecimal()

str.isdecimal() 判断文本中是否只有数字（全角或者半角），如果有小数点，就返回False。

运行结果几乎与str.isdigit() 一致，只是b"3".isdecimal()返回的False，而isdigit()是True。

str.isdecimal()可以用于对输入项要求是自然数的内容的判断。只是byte类的数字返回False。

③str.isnumeric()

str.isnumeric()，相比str.isdigit()，不支持byte类的数字，但是支持Unicode 数字。

"3".isnumeric() -->True "-3".isnumeric() -->False b"3".isnumeric() -->False "030".isnumeric() -->True "０３０".isnumeric() -->True "3.0".isnumeric() -->True "三零".isnumeric() -->True "三十".isnumeric() -->True "叁".isnumeric()