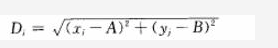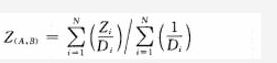IDW（反距离里加权插值）
假设 距离较近的事物要比距离较远的事物更相似。
当为任何未测量的位置预测值时，反距离权重法会采用预测位置周围的测量值与距离预测位置较远的测量值相比，距离预测位置最近的测量值对预测值的影响更大。反距离权重法假定每个测量点都有一种局部影响，而这种影响会随着距离的增大而减小。由于这种方法为距离预测位置最近的点分配的权重较大，而权重却作为距离的函数而减小，因此称之为反距离权重法。
原理：
1.计算所有离散数据点与所求网格点的距离，在二维平面空间，离散点（xi,yi）到网格（A,B）的距离Di为：

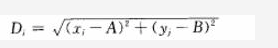
2.找出离网格点（A,B）最近的N个离散点的距离，则网格点（A,B）上的估算值为：

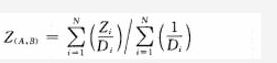
其中，Zi为离散点i上的观测值，Z(A,B)为网格点（A,B）上的估算值。

设网格点的x,y 分别为lon,lat,离散采样点的集合为：lst

def get_h(lon, lat, lst):
    p0 = [lon, lat]
    sum0 = 0
    sum1 = 0
    temp = []
    # 遍历获取该点距离所有采样点的距离
    for point in lst:
        if lon == point[0] and lat == point[1]:
            return point[2]
        Di = distance(p0, point)
        # new出来一个对象，不然会改变原来lst的值
        ptn = copy.deepcopy(point)
        ptn.append(Di)
        temp.append(ptn)
    # 根据上面ptn.append（）的值由小到大排序
    temp1 = sorted(temp, key=lambda point: point[3])
    # 遍历排序的前15个点，根据公式求出sum0 and sum1
    for point in temp1[0:15]:
        sum0 += point[2] / point[3]
        sum1 += 1 / point[3]
    return sum0 / sum1
# 计算两点间的距离
def distance(p, pi):
    dis = (p[0] - pi[0]) * (p[0] - pi[0]) + (p[1] - pi[1]) * (p[1] - pi[1])
    m_result = math.sqrt(dis)
    return m_result
参考：
 https://my.oschina.net/u/4581316/blog/4815801
 https://www.freesion.com/article/948976203/
 https://cloud.tencent.com/developer/article/1763070
                    IDW（反距离里加权插值）假设 距离较近的事物要比距离较远的事物更相似。当为任何未测量的位置预测值时，反距离权重法会采用预测位置周围的测量值与距离预测位置较远的测量值相比，距离预测位置最近的测量值对预测值的影响更大。反距离权重法假定每个测量点都有一种局部影响，而这种影响会随着距离的增大而减小。由于这种方法为距离预测位置最近的点分配的权重较大，而权重却作为距离的函数而减小，因此称之为反距离权重法。原理：1.计算所有离散数据点与所求网格点的距离，在二维平面空间，离散点（xi,yi）到网格（A,B）的距离
				
反距离权重插值适用于整个研究区数据均匀分布，不存在聚类的情况，效果最优！
插值步骤
步骤一：启动地统计向导，选择确定性方法中的反距离权重法，选择插值的源数据集和数据字段，如有必要，可添加权重字段，完毕后进入下一步。
步骤二：常规属性中，优化幂参数，搜索邻域中，设置最大最小相邻要素数，以及扇区类型，长半轴、短半轴和角度（此步的设置是之前章节介绍的向异性中各参数的探索结果），设置完成，单击下一步。