然后开始计算下一个节点属性划分后的信息增益，先以“色泽”为例，对“色泽”的每一个属性值计算信息熵，然后各个属性值加权平均得到划分后的信息熵：

按此思路计算当前节点所有属性的信息增益并比较，选择增益最大的作为当前节点的划分属性

缺点：信息增益会倾向于选择取值范围大的属性，比如把编号作为属性，只有一层就可以全部分类，

上面这一步如果采用编号划分，划分后的熵就变成0了，每一个属性划分后都是十分确定的，只有一个种类。

2. 信息增益率 C4.5

信息增益率基于信息增益进行优化，避免偏好于属性值较多的属性。

主要做法就是对属性的离散度也计算一个熵，用信息增益除以这个熵。

这样信息增益就起到一定的抑制，但是会大大增加了计算，效率下降。

所以通常先计算信息增益，从信息增益较大的前一个或者是高于平均水平的，再计算信息增益率，选择最高的

3. 基尼指数 CART (classification and regression tree)

下面是基尼指数的计算公式，需要满足 k =1 K pk =1

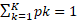
基尼指数越小，数据集的纯度越高。

对当前节点的每一个属性划分后的小份计算基尼指数，然后加权平均

选择是划分后基尼指数最小的属性作为当前节点划分属性。

再补充一点，单个节点如果特征值是连续值，比如年龄，如何对连续值进行划分是一个问题，

当然如果提前做了更合理的手工特征工程那就没有这个问题了，

关于连续值离散化的作用可以参考我的另一篇 https://blog.csdn.net/weixin_42175217/article/details/105139056

如果在决策树想要直接输入连续值呢？上面讲的都是在不同特征间选择，那么对于连续值的特征，

首先要确定该特征如何离散化才能计算出该节点的gini指数，才能横向比较。

这一步的一般方式：

• 首先对这个连续变量排序。比如年龄，把所有样本中年龄的数值从小到大排序。
• 在数据没有重复的假设下，如果有n个样本，那么排序后的数据之间应该有n-1个间隔。
• 决策树会对这n-1个间隔进行逐一尝试（分叉），每一个不同的分叉，会带来不同的gini指数，然后选择

gini指数最小的那个分叉作为最优分叉，也就是阈值。

对于决策树来说，过拟合通常就是每一个样本都落在单独的叶子节点，决策树把训练数据给背下来了

在决策树中抑制过拟合的方法就是剪枝

剪掉一些不必要的分支来降低过拟合风险，通常有预剪枝与后剪枝两种

顾名思义，提前终止某些分支的生长。

1. 可以预设树的高度，当决策树的高度达到预设值之后，停止继续构建
2. 设定叶子阈值，当叶子节点里的实例数量小于阈值时，停止
3. 设定增益阈值，当当前节点最大信息增益小于阈值，则停止

速度快，计算量小

视线短浅，比如一棵完整的决策树有层， A->B->C->D->E. 从B->C的过程中模型几乎没有什么提升，但是从C->D过程中准确度提升明显，这种情况使用预剪枝，会使模型提前终止

欠拟合风险增加

即生成一棵完全树，再回过头来剪枝。

常见方法是错误率降低剪枝，对所有非叶子节点进行剪枝计算，如果剪枝后再验证集上错误率有下降，那么就剪掉这一节点

效果一般优于预剪枝

数据量少时容易过度剪枝，某些在训练集中有的特征，验证集中不存在，出现过拟合

开局一张图总体流程： 自根至叶的递归过程 在每一个中间节点寻找一个划分属性终止条件： 当前节点包含的样本全属于同一类别，无需划分 当前属性集为空，或者所有样本在所有属性上取值相同，无法划分 当前节点包含的样本集合为空，不能划分本文以周志华老师的西瓜书中的西瓜筛选作为案例那么重点就在于如何选择每一个中间节点的划分属性了。... 决策树 算法是一种逼近离散函数值的方法。它是一种典型的 分类 方法，首先对数据进行处理，利用归纳算法生成可读的规则和 决策树 ，然后使用决策对新数据进行分析。 决策树 算法的核心思想就是通过不断地决策来筛选出最终想要的结果，来看下面一个例子： 上图是一个女孩相亲中确定见不见男方的过程，她先根据年龄筛选，年龄大于30 的不见，小于30的看长相；长相丑的不见，不丑的见……