散度和旋度的物理意义是什么？

能用稍微形象的例子来解释吗？普通工科学生的理解力能明白的。
关注者
2,479
被浏览
388,705

37 个回答

我在数学书中看到散度和旋度的时候，如果不结合物理来理解这两个数学公式的话，不过是平平无奇的曲线积分、曲面积分的一个应用而已。数学书上提到这两个公式的目的应该也是为了加深对曲线积分、曲面积分的理解。

有句名言怎么说的来着：

数学没有物理是瞎子，物理没有数学是跛子

下面就让我们结合物理来理解下 散度和旋度 。我是学数学的并非学物理的，我之后涉及的物理知识很可能是非常直觉的、不严格的，望大家多多包涵。

1 通量与散度

要理解散度，先要理解通量。

1.1 通量

通量简单来说，就是单位时间内通过的某个曲面的量。

1.1.1 太阳辐射与通量

听起来有点抽象，我们举个例子：

我们都知道，人类离不开太阳。因为每时每刻我们都在接收太阳带给我们的能量。那太阳每秒钟到底会向外辐射多少能量呢？

一种比较直观的办法，就是计算到底有多少能量通过太阳的表面。什么意思呢？

这个有着耀眼光芒的就是太阳：

为了方便观看，我们只看它在二维平面上的投影图，这并不影响我们的讨论：

太阳每时每刻都在向外辐射能量。

沿着太阳表面，作一条封闭曲线（其实是封闭的曲面，因为太阳实际上是一个球体）：

粗略来说，我们把曲面上的 \vec{A} 给加起来就是通过此曲面的通量。

但是这里有个细节问题， \vec{A} 在曲面上的不同的点的方向是不一样的，我们应该怎么相加？

1.1.2 \vec{A} 的方向

这里用太阳辐射的模型不太好说明，我们换一个模型来描述。

我有一间房子，请无视我的灵魂画法：

为了方便数学建模，我把它表示为一个多边形：

屋外下着垂直于地面的雨滴：

如果屋顶有一个天窗忘了关，地面就会有一滩水渍：

如果是侧面的屋顶有同样大小的天窗忘了关，地上的水渍就会小一些：

如果是在垂直的墙壁上的窗户忘了关，可以想见，地上是不会有水渍的。

可以观察到，水渍在雨水和窗户垂直的时候取到最大值，相切的时候取到最小值。在中间的时候水渍的大小是窗户在与雨水垂直方向的投影。

所以我们只需要关注 \vec{A} 垂直于曲面的分量就可以了：

1.1.3 小结

根据上面所述，通量就是把曲面上的 \vec{A}\cdot\vec{n} 通过积分积起来。

我们很容易推出，对于曲面 \Sigma ，它的通量为：

\mathop{\iint}_{\Sigma}\vec{A}\cdot\vec{n}dS

1.2 散度

实际上还有一种计算太阳表面辐射的办法，只是这个办法有点局限性，如果我们计算的表面不封闭的话就不能用，比如下面这样只计算一半的曲面的通量的话就不能使用：

为什么不能用？你看了后面的讲解就可以知道了。

我们知道，其实太阳之所以会产生辐射，是因为太阳内部随时都在发生核聚变。

当然了，每时每刻有许许多多的点都在发生核聚变。

粗略地说，因为我们要计算整个太阳表面的辐射，每个点核聚变产生的辐射最终都会穿过太阳表面，因此我们把每个点的辐射加起来就可以得到太阳的表面辐射，即通量了。

当然，如果我们像之前说的一样只计算太阳一半的表面辐射的话，那么我刚才说的就不成立了。

为了通过这个思想来计算通量，我们就需要知道每个点的辐射强度（这其实就是高斯公式了），那么如何计算每一点的辐射强度呢？

根据微积分的基本思想，把将之前的封闭曲面缩小到极限为0，即几乎和辐射点重合时，用此时的通量，除以封闭曲面所围体积，就能得到此点的强度：

而此点的辐射强度就是 散度 。

所以散度的公式我们也很好推导，假设要求在向量场 \vec{A} 中 M 点的散度：

\displaystyle div\vec{A}(M)=\lim_{\Omega\to M}\frac{1}{V}\int\!\!\!\!\int_{\Sigma}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\;\;\;\bigcirc\,\,\vec{A}\cdot \vec{n}dS

其中， \Omega 为封闭曲面 \Sigma 围成的区域， V 为 \Omega 的体积。

1.3 散度以及通量的符号

介于散度和通量的关系，所以下面就只介绍散度的符号，通量是一样的道理。

比如对于太阳中正在进行核聚变的点：

太阳中，有些点并不产生核聚变（有可能此点是真空），辐射只是经过此点：

而黑洞，能量进去了就不会出来，那么它的散度就为负。

好了，以后说“正能量”，可以文艺点说，“散度为正”。

2 环流量与旋度

环流量、旋度和通量、散度挺像的，下面的讲解就比较简略了，可以对比理解。

中国有句名言叫"水能载舟，亦能覆舟"。描述的是水的威力。

不过水不仅能使船上下颠簸，而且还能让船旋转。

为了描述旋转，我们就有了 环流量和旋度 。

2.1 环流量

环流量简单来说，就是单位时间内环绕的某个曲线的量。

我下面描述的都是在二维向量场中的情况，三维向量场中的情况类似，但是要更复杂一些。

比如，这是一汪湖水，其中箭头所指方向为水流方向，长短为水流的力量大小：

要计算一艘船在水流中受到多少旋转的力，就把这艘船丢到水里去。

船的轮廓曲线抽象为封闭曲线，我们称为 \Gamma :

单位时间内，这艘船在水场中受到旋转的力就称为环流量。

对于一个圆，我们可以比较直观的感受到：

所以和通量类似的，我们只需要切线方向的力：

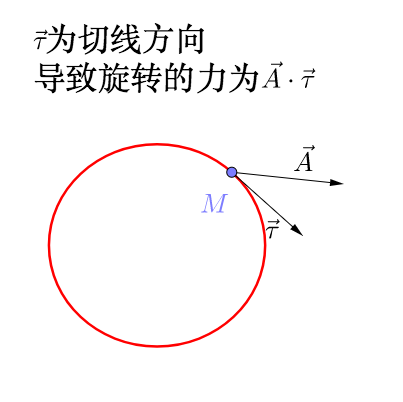
因此整个环流量的表达式为：

\oint_{\Gamma}\vec{A}\cdot\vec{\tau}dl

2.2 旋度

类似于通量，我们也可以把各个点环流量的强度加起来，得到环流量。

而通过不断缩小封闭区域就可以得到环流量的强度，即旋度：

我们也很容易推出此点旋度， M 点的旋度表达式为:

\displaystyle\lim_{\Sigma\to M}\frac{1}{S} \oint_{\Gamma}\vec{A}\cdot\vec{\tau}dl

其中， \Sigma 为封闭曲面 \Gamma 围成的区域， S 为 \Sigma 的面积。

当然，旋度还有方向，下面再解释一下方向。

2.3 方向

旋转都是有方向的，那么封闭曲线是顺时针还是逆时针旋转呢？

先看看什么是右手定则：

大拇指所指方向为旋度的方向，知道大拇指的方向就知道封闭曲线是顺时针还是逆时针旋转了。

维基百科上有一幅图特别直观，一架农业飞机翼尖激起的气流。烟雾成顺时针或逆时针方向运动，对应的旋度在飞机前行的方向上：


3 总结

通过物理来理解这四个概念还是比较容易的。

  • 通量是单位时间内通过的某个曲面的量
  • 散度是通量强度
  • 环流量是单位时间内环绕的某个曲线的量
  • 旋度是环流量强度

其实，这些概念本来就是在物理学领域产生的，物理学家发明完了之后，就问数学家，“您看怎么计算？”

数学家翻一翻白眼，你知不知道这得死多少脑细胞！！

为了计算这些，又吭哧吭哧的发展出了各种曲线、曲面积分，格林、高斯、斯托克斯等公式。哎，收拾残局的总是数学家。

散度是描述矢量场中某一点是发散还是汇聚的，就是这一点的无限小体积元内是进来的矢量多还是出去的矢量多。旋度是描述矢量场中某一点所包含微元在场中的旋转程度。