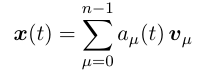[知识点笔记]拉普拉斯矩阵在网络热扩散中的应用
拉普拉斯矩阵在网络热扩散中的应用
1. 研究对象
这里的研究对象不局限于词汇, 包含各种类型的信息网络以及社会网络等等.
这些网络有一个特性就是 : 节点之间拥有非对称关系. (当然也有完全对称的)
并且本文研究的图对象是 无向图
2. 拉普拉斯矩阵
2.1 Graph的表征方法
邻接矩阵去表示Graph.
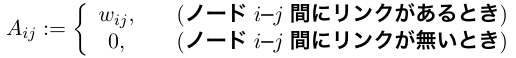
在无向图的时候, 这个矩阵是对称矩阵, 因为 w_{ij}=w_{ji}
2.2 拉普拉斯矩阵定义
D: 度矩阵
A: 邻接矩阵
L: 拉普拉斯矩阵
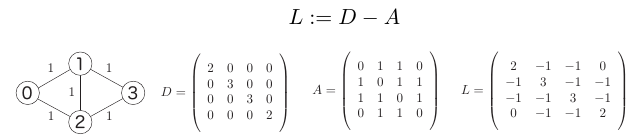
2.3 拉普拉斯矩阵性质
1) 实对称矩阵拥有的性质
- L 的特征值有n个, 并且都是实数
- L 的特征向量组成单位正交矩阵
2) 特有的性质
-
L是半正定矩阵, 即特征值均大于等于0
证明: 见 讲义 2.2部分 - 特征值为0的情况代表有互相不连接的子图, 特征值0的个数代表的就是互相无连接子图的个数.
- 最小的非0特征值代表着图的连接强度, 这个特征值被称为 Algebraic connectivity.
- 非独立于节点数目
- 在随机图中, Algebraic connectivity 随着平均度数增加而增加, 随着节点数减少而减少.
-
将非0最小的特征值对应的特征向量称为Fiedler向量.
它代表了最佳图划分的一个解(即势函数), 至于为什么下面会讲.
3. 网络信息(热)传导
下面考虑信息在网络上的传导过程.
3.1 热传导
我们最终的目的是将 信息流在网络中的传导 类比为 能量在网络空间中的扩散
那么先来看下能量的传导方式, 下面是wiki关于热传导的介绍:
1) 热传导的直观感觉

可以看出, 热传导是一种从中心向四周扩散, 并且逐渐减慢速度的过程.
三维空间中的热传导可以发生在多种介质之间, 例如在水中融化的冰, 由于水的导热系数随温度变化而有所变化, 所以其周围的传导率是一直变化的.
2) 热传导方程
我们是用一个三维的偏微分方程来模拟三维空间中的热传导过程的.
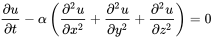
也就是 :
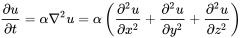
将其扩展到更高维空间中就是:
\frac{\partial u}{\partial t}-\alpha \nabla^{2}u=0
其中
- u = u(x, y, z, t)
- \frac{\partial u}{\partial t} 指的是温度关于时间变化的速率
- 关于空间上的变化可以看出是二次的, 那么 u_{xx}, u_{yy} 和 u_{zz} 就是二次偏导.
- \alpha=k/c_p\rho 是热传导率, 依据材料不同而变化
3) 热传导方程的解
对于n-variables的情况:
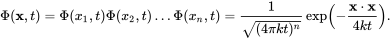
对于1-variable的情况:
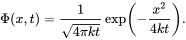
3.2 在网络上的热传导
1) 网络上的特点是:
- 每个节点都是一个能量源 x_i(t)
- 不同节点之间的能量不同, 能量要从高的节点流向低的节点. 移动的速度和两个节点之间的能量差成正比 \propto |x_i(t)-x_j(t)|
- 不同节点之间的连接通路是不同的, 拥有不同的传导率.
这里我们就知道了一个很重要的提示, 就是两个节点能量的差 |x_i(t)-x_j(t)|
2) 网络上的传导速率
设t时刻的能量(信息)分布为 x(t)=(x_0(t),x_1(t),...,x_{n-1}(t)) .
网络传导微分方程为:
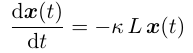
其中 κ 是热传导速率, 在这里就是两点间的距离. 由于这里假设的 x_i(t) 是一个标量, 因此这一个一维空间的热传导问题.
回顾一维热传导的公式:
这里由于公式来源不同, 将热量公式 u(x,t) 换为了 p(x,t)
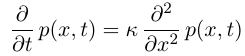
(这里缺个负号)
注意两个式子的右边, 可以看到, 拉普拉斯矩阵 L 的效果是等于 \partial^2/\partial x^2 的效果.
不过这里也有不同的地方:
网络传导的位置是固定的, 体现在网络传导方程右边的式子的变量只有 t.
4. 拉普拉斯用于网络信息传导
4.1 网络势能
设点 i 包含的初始信息为 x_i . 那么这个节点拥有的信息量就是 |x_i| .
- 这里的 x_i 是一个标量, 因此,这是一个在一维空间上的能量扩散问题, 因为没有方向
-
如果是向量的话会有什么结果?
如果是向量的话, 这里的信息和热量能量等等不同, 他是一个有方向的向量, 其实这个方向就代表了包含着位置信息, 也就是3节中的 x,y,z .
- 根据网络特点2 : 两个节点拥有的信息差就是 |x_i-x_j|
- 根据网络特点3 : 对于无向图而言, 节点之间的连接通路多是指其最短距离, 那么距离越远连通性越差, 传递就越慢.
- 根据热传导的关于位置的二次性
综合以上三点, 有了以下公式:
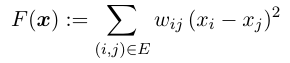
这里的 x=(x_0,x_1,...,x_{n-1})^T , 是一个向量. 因此 F(x) 就是整个网络中的信息传递速率, 也就是势能, 注意是整个网络的, 描述的是整个网络中的势能
4.2 拉普拉斯二次形式
F(x) 其实可以转换为拉普拉斯二次形式, 如下:
- f^TLf = f^TDf - f^TWf = \sum\limits_{i=1}^{n}d_if_i^2 - \sum\limits_{i,j=1}^{n}w_{ij}f_if_j
- d_i=\sum_j^{|E|} w_{ij}
- x^TLx =\frac{1}{2}( \sum\limits_{i=1}^{n}d_ix_i^2 - 2 \sum\limits_{i,j=1}^{n}w_{ij}x_ix_j + \sum\limits_{j=1}^{n}d_jx_j^2) \\=\frac{1}{2}( \sum\limits_{i,j=1}^{n}w_{ij}x_i^2 - 2 \sum\limits_{i,j=1}^{n}w_{ij}x_ix_j + \sum\limits_{i,j=1}^{n}w_{ij}x_j^2) \\= \frac{1}{2}\sum\limits_{i,j=1}^{n}w_{ij}(x_i-x_j)^2
因此, 网络的势能可以用 x^TLx 来进行表示.
这里的 x 储存了各个点的能量信息, 是一个能量分布向量.
4.3 解最优化问题
这里我们设网络的所有信息总和为1. 那么就有 |x|=1 .
我们要在这个情况下求
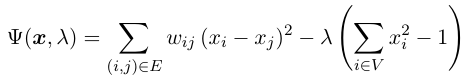
其中, \lambda 是拉格朗日乘数.
根据拉格朗日乘数法的要求
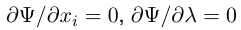
有:
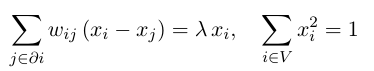
将式子整合起来就是:
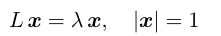
4.3节最后解的意义, 我并没有搞清楚. 搞清楚的还望提示.
5. 求解热传导方程
这一节我们将解释拉普拉斯矩阵特征值的含义.
5.1 一维热扩散微分方程的解
1) 傅里叶变换
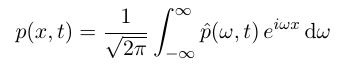
这一步将目标函数转换为了无数热量函数的和. 对原式进行了分解.
2) 代入扩散方程
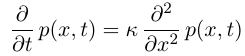
(这里缺个负号)
得:
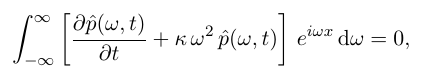
因此, 对每一个 w 都要有, 因此拆除了无限个:
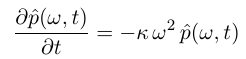
3) 对每一个微分方程求解
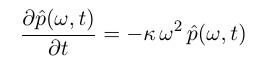
得出无数个:
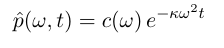
5.2 网络上的扩散公式
1) 利用特征值分解展开
原扩散方程是:
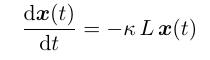
其中, 利用拉普拉斯矩阵 L 对角化的基底将 x(t) 展开:
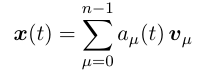
其中, v_{\mu} 是对应着特征值 \lambda_\mu 的特征向量.
2) 代入扩散方程
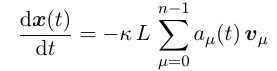
由于 v_{\mu} 是 L 的特征向量, 因此:
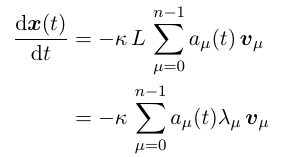
对于每个特征向量, 就有如下一个微分方程, 因此共有n个这样的微分方程, n是节点数:
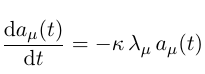
3) 对每一个微分方程求解
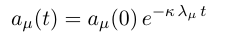
5.3 对网络扩散的分析
- 这里通过先将 0 时刻的 x 分散为不同拉普拉斯矩阵对角化基底(特征向量) x(0)=\Sigma_{\mu=0}^{n-1}a_\mu(0)v_\mu
- 然后, 每个基底方向都有一个扩散速度,这个就是最后的微分方程的解, a_\mu(t) .
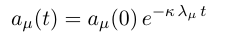
- 算出每个基底方向的热扩散值后, 在通过拉普拉斯矩阵对角化特征值变换回 x(t)