ylabel('f(x)');
f=@(x)(x.^2.*sin(x)-x+1);
[m, n]=fzero(f,-2); %在x=-2附近求函数零点,m是零点的x坐标,n是零点的y坐标(注意:Matlab默认求出的是弧度值!)
注意:[m, n] = fzero(funHandle, x0)表示在x0附近求funHandle函数句柄的零点,返回的m是求出的零点的x坐标,n是求出的零点的y坐标。其中函数句柄可以用下面的两种方法表示:
一元函数:
f=@(x)(...)
如:f=@(x)(2*x.^2+5*x-15)
二元函数:
f=@(x, y)(...)
如:f=@(x, y)(sin(x.^2+y.^2))
一元函数:
f=inline('f(x)', 'x') 其中f(x)是函数表达式,x是该函数表达式中的自变量
如:f=inline('2*x.^2+5*x-15', 'x')
二元函数:
f=inline('f(x)', 'x', 'y') 其中f(x)是函数表达式,x,y是该函数表达式中的自变量
如:f=inline('sin(x.^2+y.^2)',
'x', 'y')
注意:定义好函数句柄后就可以按下面的方法使用:f(10)表示求x=10的函数值
roots:
roots可以求一元多项式函数(诸如
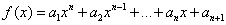 的形式)的所有零点:
的形式)的所有零点:
o=roots([1 0 -2 -5]);
输出三个零点,包括两个复数
注意:o=roots(m)中m表示该多项式的各阶系数(阶数从大到小排列),输出的o是一个一维列向量,表示求出的所有零点(包括复数)
fsolve:
fsolve可以求出二元函数的零点:
 的零点(从[-5, -5]处开始搜寻)(fsolve采用迭代法求零点,因此需要设定一个初始值):
的零点(从[-5, -5]处开始搜寻)(fsolve采用迭代法求零点,因此需要设定一个初始值):
首先我们要把上面的每个方程化为
 的形式,然后输入:
的形式,然后输入:
f=@(x)([2*x(1)-x(2)-exp(-x(1)); -x(1)+2*x(2)-exp(-x(2))]);
y=fsolve(f,[-5 -5]);
y=[0.5671 0.5671]
1.0e-006 *
-0.4059
-0.4059
可见y=[x1, x2]的确非常接近零点
Matlab之函数零点Matlab中求函数零点的函数是fzero(一元函数),fsolve(二元函数),roots(一元多项式)等:fzero:fzero可以求任何一元函数的零点:求函数的零点:x=-3:0.1:4;y=x.^2.*sin(x)-x+1;plot(x, y, 'r'); %绘出图形grid on %显示网格line(...
x = fsolve(f, x0)
上面的代码使用了 fsolve
函数
,并将被
求
解的
函数
f 和初始猜测值 x0 作为输入。fsolve
函数
会返回
函数
f 的
零点
,即 x 值,使得 f(x) = 0。
如果
函数
有多个
零点
,可以重复使用 f...
matlab
利用fzero
求
零点
f = @(x)x.^5-2*x-5; %注意
函数
的书写格式
z = fzero(f,[-1000 1000]) 主要学习一下书写格式,
函数
也可以另建文件这样写function y=f(x)
y=1/(1+x^2);
一、符号方程
求
解
在
MATLAB
中,
求
解用符号表达式表示的代数方程可由
函数
solve实现,其调用格式为:
solve(s)(
求
解符号表达式s的代数方程,
求
解变量为默认变量,当方程右端为0时,方程可以不标出等号和0,仅标出方程的左端)
solve(s,v)(
求
解符号表达式s的代数方程,
求
解变量为v)
最大预设
零点
问题的
matlab
代码计算机视觉预热
使用
MATLAB
对图像文件进行基本的计算机视觉操作
[1分]将图像Peppers.bmp加载到变量A中。在图1上显示加载的图像A,并以消息“
Original
Image”作为图标题。
{认为:A的数据类型是什么?
A的大小是多少?}
Matlab
提示:读,图,显示,标题,显示,暂停
[5分]将图像A转换为灰度图像并将其存储为B。将图像B换位为TB。
将图像B作为HB水平翻转,以使B的上半部分成为HB的下半部分,而B的下半部分成为HB的上半部分。
将图像B的列在左右方向上翻转为FB。
在图2上显示图像B,TB,HB和FB,其中B位于左上,TB位于右上,HB位于左下,FB位于右下。
用其对应的矩阵名称(例如B,TB,HB和FB)标记每个图像。
Matlab
提示:rgb2gray,转置(或'),子图,fliplr,flipud,flipdim
[10分]通过分别调用适当的
Matlab
内置
函数
,将B的最大,最小,均值和中值强度值保存在适当的变量中。
编写一个
Matlab
函数
FindInfo来计算灰度输入图像的最大,最小,均值和中值强度
matlab
函数
大全-
matlab
函数
大全.doc
比较白痴的东西,不过对初学者也许有用,特分享一下。不要喷我哦!
函数
具体用法可以用help查一下。附件内容与下面一样的。
Aabs 绝对值、模、字符的ASCII码值
acos 反余弦
acosh 反双曲余弦
acot 反余切
acoth 反双曲余切
acsc 反余割
acsch 反双曲余割
align 启动图形对象几何位置排列工具
all 所有元素非零为真
angle 相角
ans 表达式计算结果的缺省变量名
any 所有元素非全零为真
area 面域图
argnames
函数
M文件宗量名
asec 反正割
asech 反双曲正割
asin 反正弦
asinh 反双曲正弦
assignin 向变量赋值
atan 反正切
atan2 四象限反正切
atanh 反双曲正切
autumn 红黄调秋色图阵
axes 创建轴对象的低层指令
axis 控制轴刻度和风格的高层指令
bar 二维直方图
bar3 三维直方图
bar3h 三维水平直方图
barh 二维水平直方图
base2dec X进制转换为十进制
bin2dec 二进制转换为十进制
blanks 创建空格串
bone 蓝色调黑白色图阵
box 框状坐标轴
break while 或for 环中断指令
brighten 亮度控制
capture (3版以前)捕获当前图形
cart2pol 直角坐标变为极或柱坐标
cart2sph 直角坐标变为球坐标
cat 串接成高维数组
caxis 色标尺刻度
cd 指定当前目录
cdedit 启动用户菜单、控件回调
函数
设计工具
cdf2rdf 复数特征值对角阵转为实数块对角阵
ceil 向正无穷取整
cell 创建元胞数组
cell2struct 元胞数组转换为构架数组
celldisp 显示元胞数组内容
cellplot 元胞数组内部结构图示
char 把数值、符号、内联类转换为字符对象
chi2cdf 分布累计概率
函数
chi2inv 分布逆累计概率
函数
chi2pdf 分布概率密度
函数
chi2rnd 分布随机数发生器
chol Cholesky分解
clabel 等位线标识
cla 清除当前轴
class 获知对象类别或创建对象
clc 清除指令窗
clear 清除内存变量和
函数
clf 清除图对象
clock 时钟
colorcube 三浓淡多彩交叉色图矩阵
colordef 设置色彩缺省值
colormap 色图
colspace 列空间的基
close 关闭指定窗口
colperm 列排序置换向量
comet 彗星状轨迹图
comet3 三维彗星轨迹图
compass 射线图
compose
求
复合
函数
cond (逆)条件数
condeig 计算特征值、特征向量同时给出条件数
condest 范 -1条件数估计
conj 复数共轭
contour 等位线
contourf 填色等位线
contour3 三维等位线
contourslice 四维切片等位线图
conv 多项式乘、卷积
cool 青紫调冷色图
copper 古铜调色图
cos 余弦
cosh 双曲余弦
cot 余切
coth 双曲余切
cplxpair 复数共轭成对排列
csc 余割
csch 双曲余割
cumsum 元素累计和
cumtrapz 累计梯形积分
cylinder 创建圆柱
dblquad 二重数值积分
deal 分配宗量
deblank 删去串尾部的空格符
dec2base 十进制转换为X进制
dec2bin 十进制转换为二进制
dec2hex 十进制转换为十六进制
deconv 多项式除、解卷
delaunay Delaunay 三角剖分
del2 离散Laplacian差分
demo
Matlab
演示
det 行列式
diag 矩阵对角元素提取、创建对角阵
diary
Matlab
指令窗文本内容记录
diff 数值差分、符号微分
digits 符号计算中设置符号数值的精度
dir 目录列表
disp 显示数组
display 显示对象内容的重载
函数
dlinmod 离散系统的线性化模型
dmperm 矩阵Dulmage-Mendelsohn 分解
dos 执行DOS 指令并返回结果
double 把其他类型对象转换为双精度数值
drawnow 更新事件队列强迫
Matlab
刷新屏幕
dsolve 符号计算解微分方程
echo M文件被执行指令的显示
edit 启动M文件编辑器
eig
求
特征值和特征向量
eigs
求
指定的几个特征值
end 控制流FOR等结构体的结尾元素下标
eps 浮点相对精度
error 显示出错信息并中断执行
errortrap 错误发生后程序是否继续执行的控制
erf 误差
函数
erfc 误差补
函数
erfcx 刻度误差补
函数
erfinv 逆误差
函数
errorbar 带误差限的曲线图
etreeplot 画消去树
串演算指令
in 跨空间串演算指令
exist 检查变量或
函数
是否已定义
exit 退出
Matlab
环境
exp 指数
函数
expand 符号计算中的展开操作
expint 指数积分
函数
expm 常用矩阵指数
函数
expm1 Pade法
求
矩阵指数
expm2 Taylor法
求
矩阵指数
expm3 特征值分解法
求
矩阵指数
eye 单位阵
ezcontour 画等位线的简捷指令
ezcontourf 画填色等位线的简捷指令
ezgraph3 画表面图的通用简捷指令
ezmesh 画网线图的简捷指令
ezmeshc 画带等位线的网线图的简捷指令
ezplot 画二维曲线的简捷指令
ezplot3 画三维曲线的简捷指令
ezpolar 画极坐标图的简捷指令
ezsurf 画表面图的简捷指令
ezsurfc 画带等位线的表面图的简捷指令
factor 符号计算的因式分解
feather 羽毛图
feedback 反馈连接
f 执行由串指定的
函数
fft 离散Fourier变换
fft2 二维离散Fourier变换
fftn 高维离散Fourier变换
fftshift 直流分量对中的谱
fieldnames 构架域名
figure 创建图形窗
fill3 三维多边形填色图
find 寻找非零元素下标
findobj 寻找具有指定属性的对象图柄
findstr 寻找短串的起始字符下标
findsym 机器确定内存中的符号变量
finverse 符号计算中
求
反
函数
fix 向零取整
flag 红白蓝黑交错色图阵
fliplr 矩阵的左右翻转
flipud 矩阵的上下翻转
flipdim 矩阵沿指定维翻转
floor 向负无穷取整
flops 浮点运算次数
flow
Matlab
提供的演示数据
fmin
求
单变量非线性
函数
极小值点(旧版)
fminbnd
求
单变量非线性
函数
极小值点
fmins 单纯形法
求
多变量
函数
极小值点(旧版)
fminunc 拟牛顿法
求
多变量
函数
极小值点
fminsearch 单纯形法
求
多变量
函数
极小值点
fnder 对样条
函数
求
导
fnint 利用样条
函数
求
积分
fnval 计算样条
函数
区间内任意一点的值
fnplt 绘制样条
函数
图形
fopen 打开外部文件
for 构成for环用
format 设置输出格式
fourier Fourier 变换
fplot 返函绘图指令
fprintf 设置显示格式
fread 从文件读二进制数据
fsolve
求
多元
函数
的
零点
full 把稀疏矩阵转换为非稀疏阵
funm 计算一般矩阵
函数
funtool
函数
计算器图形用户界面
fzero
求
单变量非线性
函数
的
零点
gamma
函数
gammainc 不完全
函数
gammaln
函数
的对数
gca 获得当前轴句柄
gcbo 获得正执行"回调"的对象句柄
gcf 获得当前图对象句柄
gco 获得当前对象句柄
geomean 几何平均值
get 获知对象属性
getfield 获知构架数组的域
getframe 获取影片的帧画面
ginput 从图形窗获取数据
global 定义全局变量
gplot 依图论法则画图
gradient 近似梯度
gray 黑白灰度
grid 画分格线
griddata 规则化数据和曲面拟合
gtext 由鼠标放置注释文字
guide 启动图形用户界面交互设计工具
harmmean 调和平均值
help 在线帮助
helpwin 交互式在线帮助
helpdesk 打开超文本形式用户指南
hex2dec 十六进制转换为十进制
hex2num 十六进制转换为浮点数
hidden 透视和消隐开关
hilb Hilbert矩阵
hist 频数计算或频数直方图
histc 端点定位频数直方图
histfit 带正态拟合的频数直方图
hold 当前图上重画的切换开关
horner 分解成嵌套形式
hot 黑红黄白色图
hsv 饱和色图
附件:[post]
x(i+1) = x(i) - f(x(i))/f'(x(i))
其中,f(x)是
求
解的
函数
,f'(x)是
函数
的导数,x(i) 是第 i 次迭代的结果,x(i+1)是下一次迭代的结果。
在
MATLAB
中,可以使用以下代码实现牛顿法:
function x = newton(f,df,x0,tol)
% Newton's method to solve f(x)=0
% input: f is a function handle, df is the derivative of f,
% x0 is the initial guess, tol is the tolerance
% output: x is the solution
x = x0;
iter = 0;
error = 1;
while error > tol
x_new = x - f(x)/df(x);
error = abs(x_new - x);
x = x_new;
iter = iter + 1;
disp(['Newton''s method with ',num2str(iter),' iterations']);
使用方法如下:
- 首先定义
函数
f(x) 和它的导数 df(x)。
- 然后定义初始猜测值 x0 和误差容限 tol。
- 最后,调用
函数
newton(f,df,x0,tol),得到
函数
零点
。
例如,对于
函数
f(x) = x^3 - x^2 + 2,可以使用以下代码:
f = @(x) x^3 - x^2 + 2;
df = @(x) 3*x^2 - 2*x;
x0 = 1;
tol = 1e-6;
x = newton(f,df,x0,tol);
运行代码之后,可以得到
函数
零点
x。
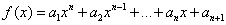 的形式)的所有零点:
的形式)的所有零点:
 的零点(从[-5, -5]处开始搜寻)(fsolve采用迭代法求零点,因此需要设定一个初始值):
的零点(从[-5, -5]处开始搜寻)(fsolve采用迭代法求零点,因此需要设定一个初始值):
 的形式,然后输入:
的形式,然后输入: