Matlab | 古诺模型求解及画图代码
古诺模型
以仅含有两个企业的古诺模型为例,该问题可叙述为:
市场上只有两家企业( 双寡头垄断 ),它们生产销售完全相同的产品,共同面临一条线性的市场需求曲线,各自 决策 能够给自己带来 最大利润 的 最优产量。
关于古诺模型的更多细节可查看课本或知乎,本文直接给出如下 算例 来展现如何求解。
算例
若市场需求函数为 p = a - b(q1 + q2) ,企业1和2的生产成本函数分别为 c1*q1 、 c2*q2^2 。求 古诺均衡 ,并 计算利润。
求解思路如下:
- 构建企业1和2的 利润函数 :价格×产量-成本;
- 同时对企业1和2的产量 求导 ,令其=0;
- 联立 两方程,求解 最优q1和q2 ;
- 将最优q1和q2表达式 代入 利润函数,得到 最优利润 。
以上四步的数学表达式和Matlab代码如下。
1. 构建企业1、2的利润函数

对应的Matlab代码为:
syms a b q1 q2 c1 c2 % 定义参数/变量
Pi1 = (a - b*(q1 + q2))*q1 - c1*q1;
Pi2 = (a - b*(q1 + q2))*q2 - c2*q2^2;可见,Matlab代码并不复杂,几乎是照抄公式,只不过所有括号均需要用 小括号 ,这个一定注意。
2. 同时对q1和q2求导,令其=0
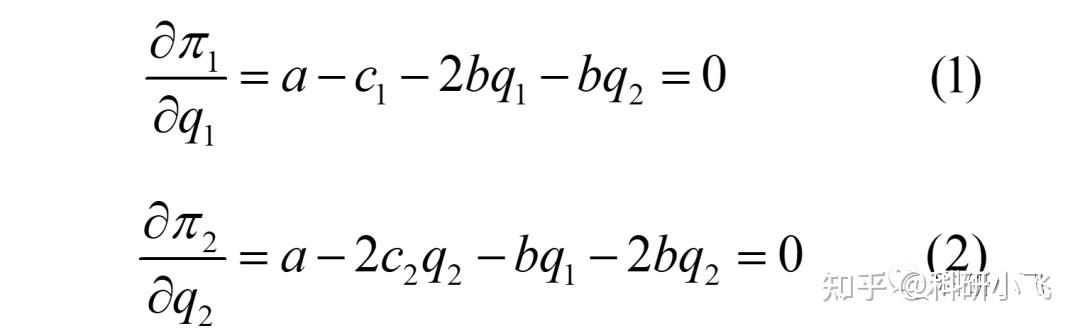
对应的Matlab代码为:
equ1 = diff(Pi1, q1);
equ2 = diff(Pi2, q2);Matlab的求导函数为 diff() ; diff(Pi1, q1) 的含义为:对利润函数Pi1中的q1变量求一阶导;求出来的算式在这里给起了个名字equ1,该名字好记就行(需符合 命名规范 )。
3. 联立方程,求解最优q1、q2

对应的Matlab代码为(一行足矣):
[Op_q1,Op_q2] = solve(equ1, equ2, q1,q2);Matlab的解方程函数为 solve() ; solve(equ1, equ2, q1, q2) 的含义为:联立两方程equ1=0和equ2=0(注:代码中=0可以 省略 ),求解两未知数q1和q2。将求得的最优q1和q2的值分别命名为 Op_q1 和 Op_q2 。
对比 手算最优值 ,用Matlab解方程只需要 一行代码 即可,大大节省科研时间。
4. 将最优q1、q2带入利润表达式
若手算,鉴于最优q1和q2表达式的 繁琐 ,带入过程可想而知地 繁琐 。
可若采用Matlab计算,也仅需要 一行代码 。
Pi1 = subs(Pi1,{q1,q2}, {Op_q1,Op_q2});
Pi2 = subs(Pi2,{q1,q2}, {Op_q1,Op_q2});Matlab的替代函数为 subs() ; subs(Pi1, {q1, q2}, {Op_q1, Op_q2} 的含义为:将 利润函数 Pi1中的q1和q2分别替换为Op_q1和Op_q2的值。
通常, 此时Pi1和Pi2的表达式会非常复杂 ,需借助Matlab的化简函数。常见的有simplify、collect、expand、factor、subexpr、pretty等。
实际上, simplify、collect和pretty 便可满足我们的绝大部分需求。
pretty(Pi1)
pretty(Pi2)此时,Matlab会返回化简好后的表达式:

即使已经非常简单,但我们还是希望能有更为直观的表现形式。此时 pretty()函数 便派上用场。
pretty(simplify(Pi1))
pretty(simplify(Pi2))此时,会得到如下呈现形式:

该形式易于抄写,非常直观。
更为方便的是,若 不想将公式手打入Word或Latex中 ,也可以调用Matlab中的latex()命令,将得到的结果复制粘贴到Word或Latex中。
latex(simplify(Pi1))
latex(simplify(Pi2))以粘贴入Word为例,分以下4步:

至此, 没动一次笔 ,便得到最优产量和利润表达式;同时,实现将表达式准确输入至Word中。
只要是 基于古诺思想的数学模型 ,均可 自动化实现以上求解 。无非就是在第一步的时候,把利润函数改成 自己的研究问题 即可。
画图
可进行的数值分析有:
- 各企业最优产量(Op_q1和Op_q2)与各参数(a/b/c1/c2)关系图;
- 比较两企业最优产量的大小,计算市场占有率;
- 各企业最优利润与各参数关系;
- 比较两企业利润大小;
- 考察利润相同下,两个参数间的变化关系等;
这里,仅以第四点为例, 考察c2变化对两企业利润的影响 。
此时,设a = 100, b = 1, c1 = 15。同时设c2取值范围为0到1,间隔0.03,即 c2 = [0: 0.03: 1] 。
注意:每一个c2都对应一个Pi1和一个Pi2,为计算所有c2对应的Pi1和Pi2,写一个 循环 即可。
clear
a = 100; b = 1; c1 = 15;
c2 = [0: 0.03: 1];
for i = 1: length(c2)
Pi1(i) = (a*b + 2*a*c2(i) - 2*b*c1 - 2*c1*c2(i))^2/(b*(3*b + 4*c2(i))^2);
Pi2(i) = ((a + c1)^2*(b + c2(i)))/(3*b + 4*c2(i))^2;
