学习索引(learned index)技术
学习索引(learned index)技术
摘要
索引技术在数据库中扮演着重要角色, 在数据库中有b tree, hash 索引等. 但是这些数据结构没有利用到被索引数据分布的信息. 本文总结了谷歌发表于NIPS 2017和SIGMOD 2018的两篇文章, 探讨如何利用机器学习技术得到更好的范围索引, 使用机器学习模型替代传统的B-trees索引, 以及在这之上的改进, 使得学习索引技术可扩展, 解决学习索引更新问题.
简介
数据库依靠索引结构来高效地执行众多核心操作. B-trees用于范围检索, Hash-Maps 用于按照键值搜索, 布隆过滤器用于判断record是否存在. 但是这些索引是广义目的的数据结构, 没有利用到被索引数据的信息, 在一些极端情况下会表现得较差, 比如当数据键值为从1递增到n, 如果使用b-tree 索引, 查询的时间复杂度为o(logn), 实际上只需要o(1)的复杂度. 同样索引的空间复杂度也只需要o(1), 而不是o(n). 如果能够学习到一个模型反映数据的模式, 就有可能自动构建索引结构即学习索引(learned index) , 进而得到显著性能提升.
Kraska[1], [2]等人提出使用机器学习模型代替传统的B树索引,并在真实数据集上取得了不错的效果,但其提出的模型假设工作负载是静态的、只读的,对于索引更新问题没有提出很好的解决办法. [3]提出了基于中间层的可扩展的学习索引模型Dabble,用来解决索引更新引发的模型重新训练问题.
内容
B-Trees可以看成模型
范围索引, 比如B-Trees, 可以视为一个机器学习模型, 给定输入Key 返回 position.
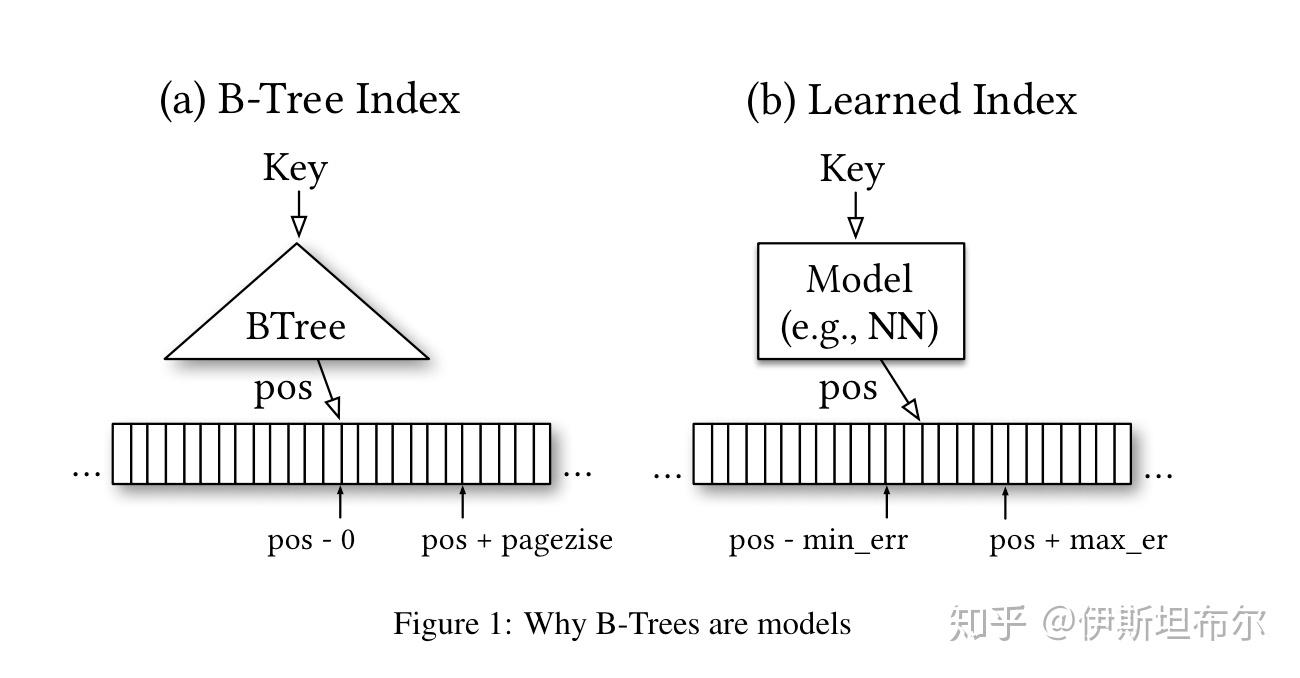
学习索引(learned index)
学习索引要做的事是学习到一个映射函数, f(key)->pos, 将key 写成x, pos写成y, 希望学习到一个模型f(x) 约等于y. 因为x 是排序过的, 所以f 实际上是在给数据的CDF建模[4]. 下图是学习索引的一个示例.
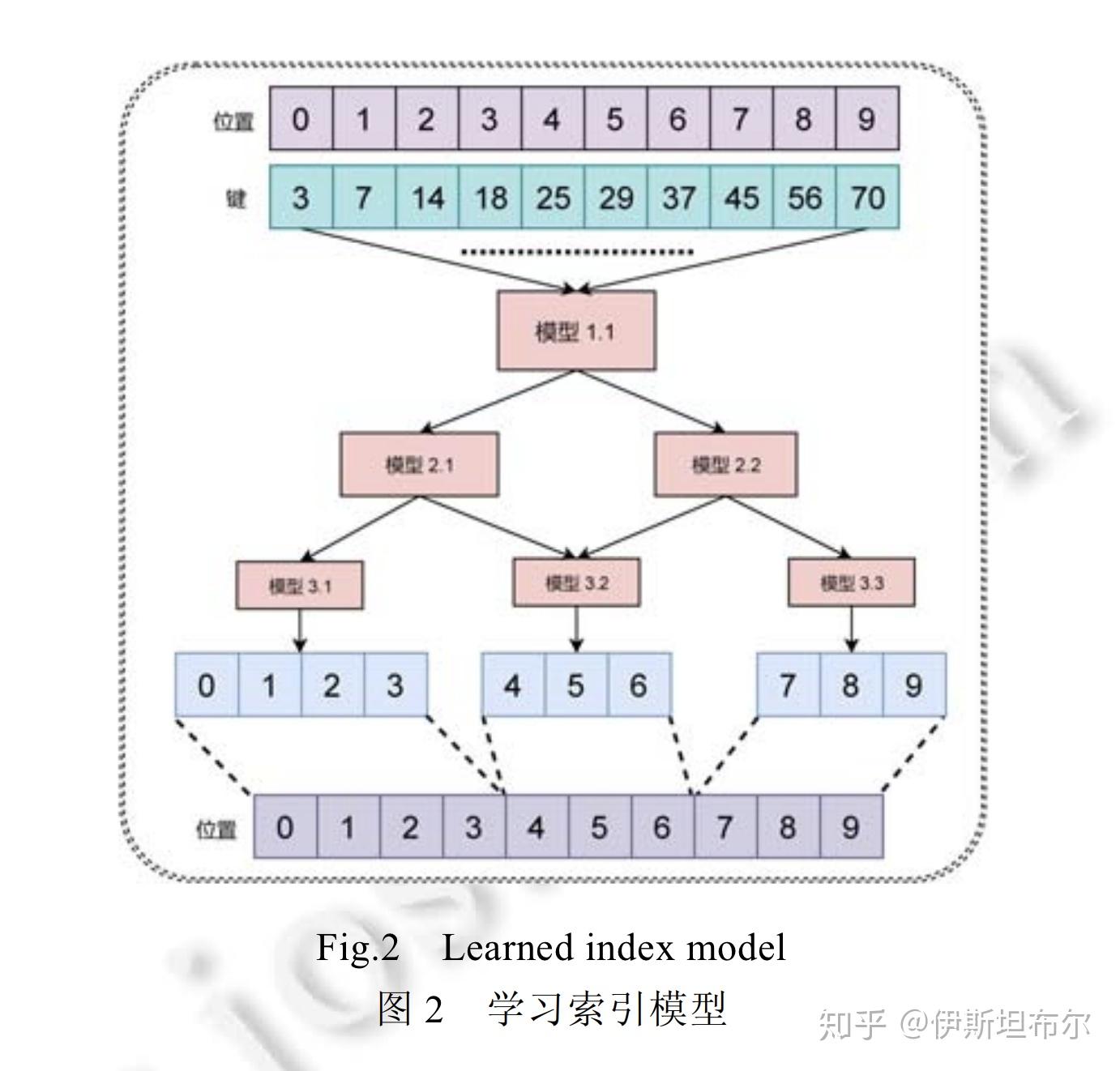
模型架构
上面的问题实质上是一个回归问题, 可以使用均方差作为损失函数, 训练模型. 同时为了提高模型的准确率, 使用层级模型. 损失函数如下所示

模型架构如下所示:
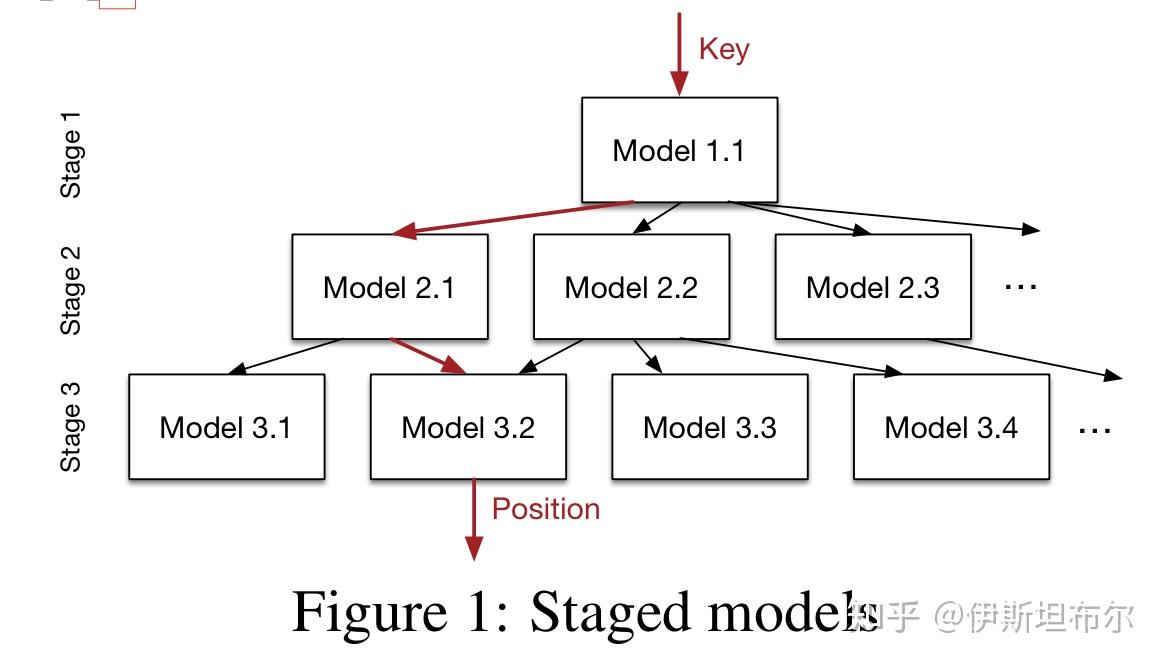
层级模型和集成模型的思路相似, 都是通过集成弱分类器得到性能更好的分类器.
学习索引(learned index)如何预测
不同于一般的机器学习任务, 在使用学习索引(learned index)的时候, 需要考虑模型输出偏差delta, 需要找到最大的误差delta_max, 在[y_pred-delta_max, y_pred+delta_max]范围内搜寻起始点, 但是这个搜寻起始点可以使用二分查找, 时间复杂度不是很高.
Dabble 模型
其提出的模型假设工作负载是静态的、只读的,对于索引更新问题没有提出很好的解决办法.提出了基于中间层的可扩展的学习索引模型Dabble,用来解决索引更新引发的模型重训练问题实验
Dabble模型中设计了3个机制:(1)利用聚类算法将数据集按照数据的聚集方式划分为K个部分, 得到K个数据区域, 使得在每一个数据区域内部, 数据分布尽可能相同; (2)对于每一个数据区域, 分别利用神经网络对其进行训练, 使网络能够对该数据区域的分布得到一个比较好的拟合; (3)在神经网络训练阶段, 重点关注访问频率高的热点数据, 从而使神经网络对这些数据的预测精度更高.另外, 为了更快地处理动态插入以及更新操作, Dabble模型提出了一种基于中间层的数据插入机制, 从而使得不同的神经网络模型之间解耦, 模型之间保持独立性.当数据插入时, 只需要重新训练有数据插入的那个数据区域对应的模型即可, 不需要对整个Dabble重新训练, 从而提高了模型的可扩展性.
Dabble 模型架构图如下所示
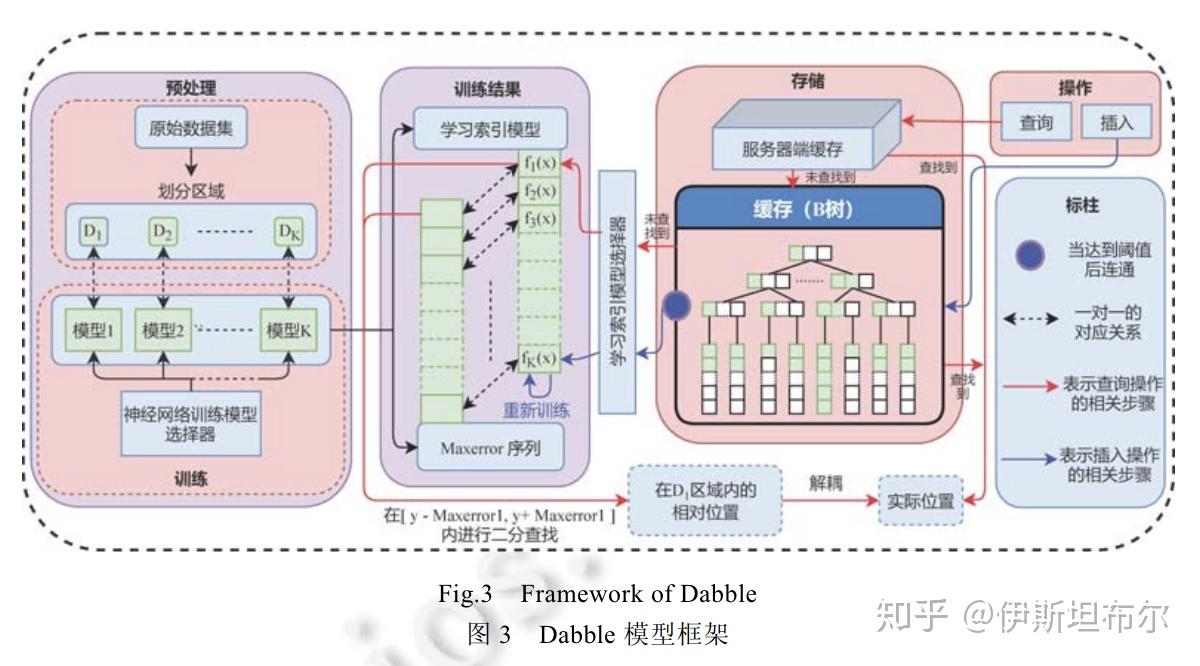
实验
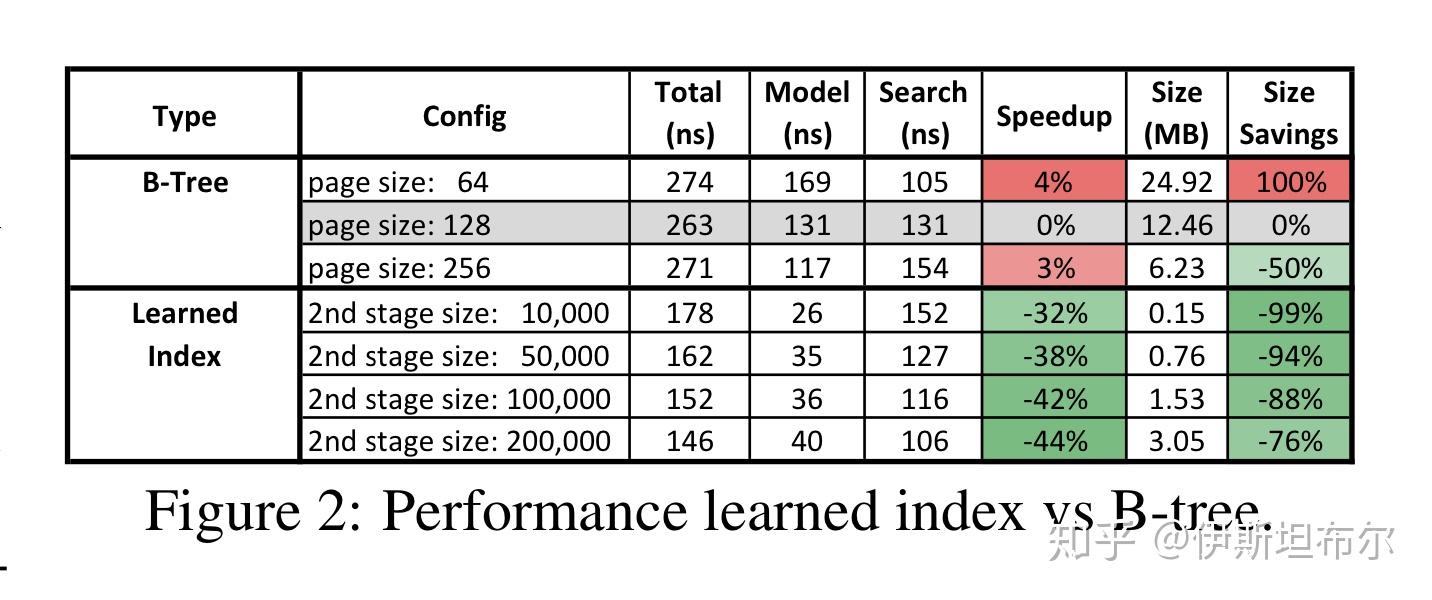
论文[1][2]在2亿网站日志数据weblogs数据集上跑了实验. 将经过cache优化过的B-Tree页大小为128作为baseline, 对于学习索引, 使用两阶段模型, 在没有GPU 和TPU 的机器上运行结果如下图所示. 可以看到学习索引比B-Tree更快的同时, 内存占用更少.
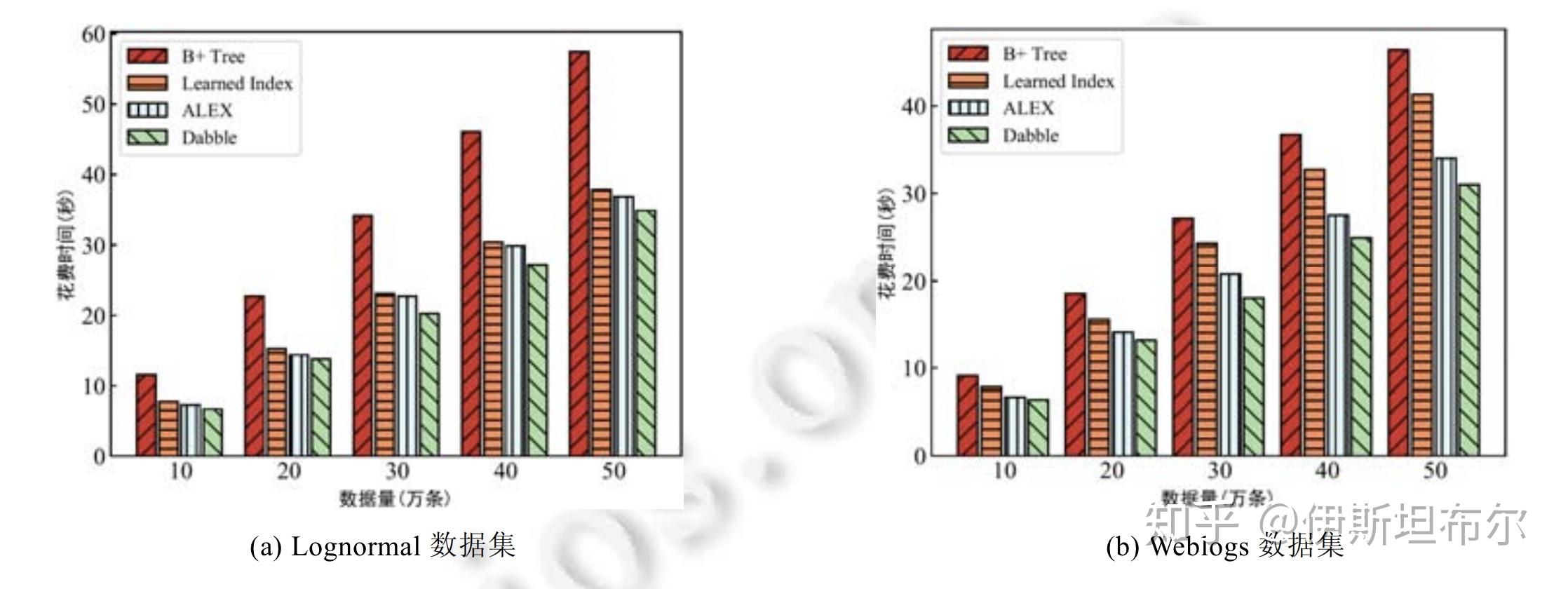
论文[3] 在weblogs 和 lognormal 数据集上进行评测, 结果如下图.
总结
本文总结了三篇文章, 主要探讨了结合机器学习技术的范围索引架构. 相较于传统的索引结构, 可学习型的索引展示了更好的可适应性.
参考文献 [1] Alex Beutel, Tim Kraska∗, Ed H. Chi, Jeffrey Dean, Neoklis Polyzotis “A Machine Learning Approach to Databases Indexes”NIPS 2017
[2] Alex Beutel, Tim Kraska∗, Ed H. Chi, Jeffrey Dean, Neoklis Polyzotis “The Case for Learned Index Structures”SIGMOD 2018
[3] 高远宁, 叶金标, 杨念祖, 高晓沨, 陈贵海. 基于中间层的可扩展学习索引技术[J]. 软件学报, 2020, 31(3): 620-633. http://www. jos.org.cn/1000-9825/59 10.htm
[4] M. Magdon-Ismail and A. F. Atiya. Neural networks for density estimation. In M. J. Kearns, S. A. Solla, and D. A. Cohn, editors, Advances in Neural Information Processing Systems 11, pages 522–528. MIT Press, 1999.
