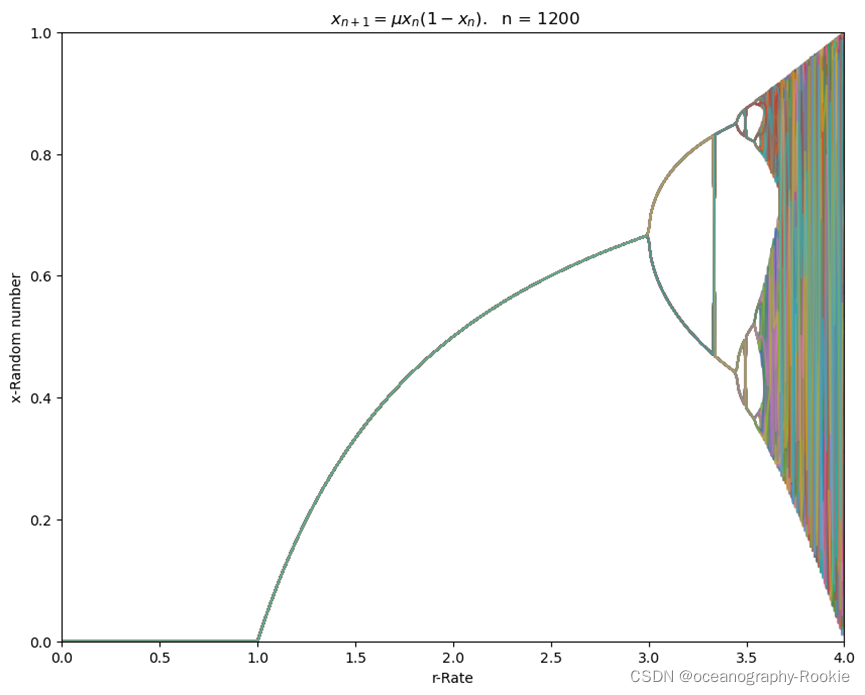
在学习非线性海洋动力学时,需要绘制一个分叉图,简单记录一下绘制过程
下面是需求,通过下面图中等式绘制分叉系统:
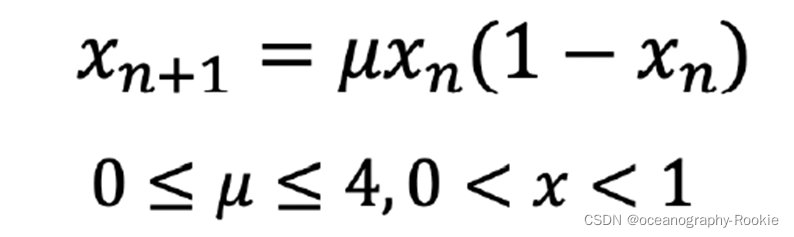
from tqdm import tqdm
import matplotlib.pyplot as plt
import numpy as np
fig=plt.figure(figsize=(10,8),dpi=100)
def LogisticMap():
mu = np.arange(0, 4, 0.01)
x = 0.1 # 初值
iters = 1000 # 不进行输出的迭代次数
last = 200 # 最后画出结果的迭代次数
for i in tqdm(range(iters+last)):
x = mu * x * (1 - x)
if i >= iters:
plt.plot(mu, x, alpha=0.5) #
plt.ylim(0, 1)
plt.xlim(0, 4)
plt.title(r' $x_{n+1} = \mu x_{n} (1-x_{n}).$ n = '+ str(i+1) )
plt.ylabel('x-Random number')
plt.xlabel('r-Rate')
plt.show()
LogisticMap()
绘制结果如下所示:
选取范围为0-4,可以发现,当r=3时,出现第一次分叉,而后继续进行分叉,直至出现混沌现象。