用C语言绘制高效率抗锯齿直线
画直线,理论上是件很简单的事,使用API就可以绘制一条条优美的直线,但是在低端嵌入式设备中无法使用API,且运行速度受到很大限制。
我尝试用不同方法实现画直线的方法,此文作为记录这段时间的优化记录,本文的主题是提升绘制直线速度。本文的代码采用 C 语言、标准库及 极简的 PNG 编码函数 svpng() ,没有使用其他 API。
在写抗锯齿直线前,先分析绘制直线的基础算法,完整代码示例: line_demo.c
1. 数值微分法(DDA算法)
void lineDDA(int x0, int y0, int x1, int y1)
int dx = x1 - x0, dy = y1 - y0, steps, k;
float xIncrement, yIncrement, x = x0, y = y0;
if (fabs(dx) > fabs(dy)) //判断增长方向
steps = fabs(dx); //以X为单位间隔取样计算
steps = fabs(dy); //以Y为单位间隔取样计算
xIncrement = (float)(dx) / (float)(steps); //计算每个度量间隔的X方向增长量
yIncrement = (float)(dy) / (float)(steps); //计算每个度量间隔的Y方向增长量
while(steps--)
setPixel(round_(x), round_(y));
x += xIncrement;
y += yIncrement;
}DDA算法是最早的画直线算法,优点:只需要对x和y不断递增就可以得到下一点的函数值,这样避免了对每一个像素都使用直线方程来计算,消除了浮点数乘法运算。缺点:还是不算快,且存在浮点计算,而且大量浮点累加,可能存在误差。
2. Bresenham算法
void lineBres(int x0, int y0, int x1, int y1,int r)
int p, twoDy, twoDyMinusDx, s1, s2;
int dx = abs(x1 - x0), dy = abs(y1 - y0);
if (dy > dx) //斜率大于1
p = 2 * dx - dy;
twoDy = 2 * dx;
twoDyMinusDx = 2 * (dx - dy);
if (y0 > y1)//斜率为负时 反转斜率
swap_(x0, x1);swap_(y0, y1);
s1 = x1 > x0 ? 1 : -1;
setPixelHorWidth(x0, y0,r);
while (y0 < y1)
y0++;
if (p < 0){p += twoDy;}
else {x0 += s1;p += twoDyMinusDx;}
setPixelHorWidth(x0, y0, r);
p = 2 * dy - dx;
twoDy = 2 * dy;
twoDyMinusDx = 2 * (dy - dx);
if (x0 > x1)//斜率为负时 反转斜率
swap_(x0, x1);swap_(y0, y1);
s2 = y1 > y0 ? 1 : -1;
setPixeVerWidth(x0, y0, r);
while (x0 < x1)
x0++;
if (p <
0) {p += twoDy;}
else {y0 += s2;p += twoDyMinusDx;}
setPixeVerWidth(x0, y0, r);
}Bresenham直线算法是目前绘制直线最快的一种算法也是我使用最多的一种,我这里优化了一下,while中只需判断一次,代码量多了一点,但速度提升了。
这两个算法的原理都比较简单,DDA使用了微分的概念,Bresenham通过引入直线方程式消除浮点计算,我这里就不详细说了,不懂的百度也能找到相关资料。
为了测试不同角度,我用了个测试用例,代码来源于这个大神: 传送门
int main() {
memset(img, 0, sizeof(img));
float cx = W * 0.5f, cy = H * 0.5f;
for (int j = 0; j < 5; j++) {
float r1 = fminf(W, H) * (j + 0.5f) * 0.085f;
float r2 = fminf(W, H) * (j + 1.5f) * 0.085f;
float t = j * PI / 64.0f, r = (j + 1) * 1.0f;
for (int i = 1; i <= 64; i++, t += 2.0f * PI / 64.0f) {
float ct = cosf(t), st = sinf(t);
lineBres(cx + r1 * ct, cy - r1 * st, cx + r2 * ct, cy - r2 * st, r);
svpng(fopen("line_dda.png", "wb"), W, H, img, 0);
}渲染结果与局部放大:


3.吴小林抗锯齿直线
这个算是直线抗锯齿中我能找到最快速度的,效果也不错,吴小林算法,在计算的每个步骤中,都对最接近像素线的两个像素进行计算,并且根据距离对它们进行不同强度的着色,比如当前直线距离上侧像素为0.8,则上侧像素强度为0.2,下侧像素强度为0.8。
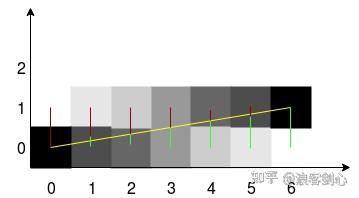
//由于像素值不能为浮点数,因此以下算法假设仅将整数坐标作为输入。因此去除了首尾点的特殊操作
#define ipart_(X) ((int)(X))
#define round_(X) ((int)(((float)(X))+0.5f))
#define fpart_(X) (((float)(X))-(float)ipart_(X))
#define rfpart_(X) (1.0-fpart_(X))
#define swap_(a,b) (a=(a)+(b),b=(a)-(b),a=(a)-(b))
void setPixelAlpha(int x, int y, float brightness)
alphablend(x, y, brightness, 255.0f, 255.0f, 255.0f);
void lineAnti_Wu(int x0, int y0, int x1, int y1)
int steep = abs(y1 - y0) > abs(x1 - x0);
// swap the co-ordinates if slope > 1 or we
// draw backwards
if (steep)
swap_(x0, y0);
swap_(x1, y1);
if (x0 > x1)
swap_(x0, x1);
swap_(y0, y1);
//compute the slope
float dx = x1 - x0;
float dy = y1 - y0;
float gradient = dy / dx;
if (dx == 0.0)
gradient = 1;
int xpxl1 = x0;
int xpxl2 = x1;
float intersectY = y0;
int x;
// main loop
if (steep)
for (x = xpxl1; x <= xpxl2; x++)
setPixelAlpha(ipart_(intersectY), x, rfpart_(intersectY));
setPixelAlpha(ipart_(intersectY) + 1, x,fpart_(intersectY));
intersectY += gradient;
for (x = xpxl1; x <= xpxl2; x++)
setPixelAlpha(x, ipart_(intersectY),rfpart_(intersectY));
setPixelAlpha(x, ipart_(intersectY)+1,fpart_(intersectY));
intersectY += gradient;
}

4.吴小林抗锯齿直线任意宽度
由于吴小林算法原本只能支持一个宽度的直线抗锯齿,虽然速度很快,但很难实用,冥思苦想后,想了个巧妙的办法,吴小林算法是计算直线两端的像素的距离差,那么直线向下平移N个单位,新的下个像素的色差还是和当前一样,即两侧像素为直线的抗锯齿像素。
假定直线宽度为N,N的上边界与N+1的距离为上侧像素的强度值,任意宽度即直线把像素分割为上下边线,上下边界处的抗锯齿强度对应与吴小林算法的上下像素,具体实现看代码

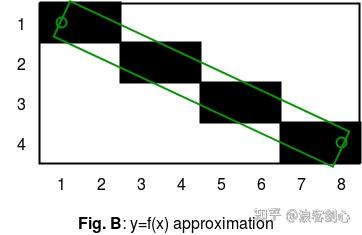
void lineAnti_WuMulti(int x0, int y0, int x1, int y1, int r)
int steep = abs(y1 - y0) > abs(x1 - x0);
// swap the co-ordinates if slope > 1 or we
// draw backwards
if (steep)
swap_(x0, y0);
swap_(x1, y1);
if (x0 > x1)
swap_(x0, x1);
swap_(y0, y1);
//compute the slope
float dx = x1 - x0;
float dy = y1 - y0;
float gradient = dy / dx;
if (dx == 0.0)
gradient = 1;
int xpxl1 = x0;
int xpxl2 = x1;
float intersectY = y0;
int i, x;
// main loop
if (steep)
for (x = xpxl1; x <= xpxl2; x++)
// pixel coverage is determined by fractional
// part of y co-ordinate
setPixelAlpha(ipart_(intersectY), x, rfpart_(intersectY));
for (i = 1; i < r; i++)
setPixel(ipart_(intersectY) + i, x);
setPixelAlpha(ipart_(intersectY) + r, x, fpart_(intersectY));
intersectY += gradient;
for (x = xpxl1; x <= xpxl2; x++)
setPixelAlpha(x, ipart_(intersectY), rfpart_(intersectY));
for (i = 1; i < r; i++)
setPixel(x, ipart_(intersectY) + i);
setPixelAlpha(x, ipart_(intersectY) + r, fpart_(intersectY));
intersectY += gradient;
}渲染效果和局部放大图:


5.区域加权抗锯齿直线任意宽度
非加权区域采样方法没有考虑,亮度不仅取决于所占的面积,还需要取决于这个物体里像素中心的远近。这里介绍加权区域采样方法。
理论参考网站: CSDN区域加权反走样 CSDN区域加权实现参考
算法原理 :将直线段看做是具有一定宽度的狭长矩形。当直线段与像素有相交时,根据相交区域与像素中心的距离来决定其对像素亮度的贡献(比重)。
计算方法 :设置相交区域面积与像素中心距离的权函数(高斯函数)反映相交面积对整个像素亮度的贡献大小,利用权函数积分求相交区域面积,用它乘以像素可设置最大亮度值,即可得到该像素实际显示的亮度值。
面积才较难算,一般采用离散化区域值进行计算
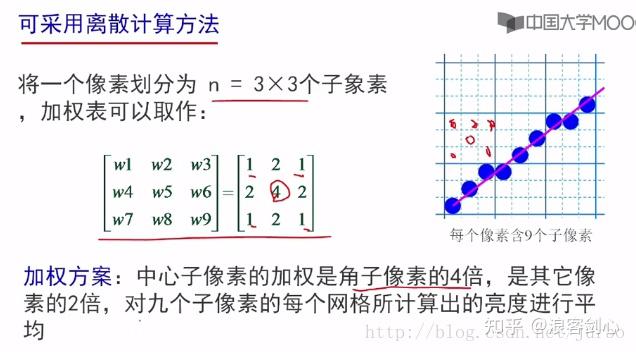
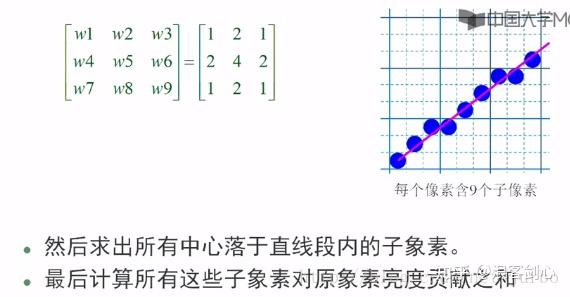
这里,我优化了非必要的抗锯齿计算,直线段为两条平行线,当0<K<1时,一根直线最多穿越两个像素,即当直线宽度为N时,也最多只需要计算4个像素的抗锯齿,极大优化了速度,如果需要边缘像素强度传递也是可以改的。
具体实现逻辑跟非加权反走样类似,只是距离计算更换为加权计算
void lineAnti_AreaWeight(int x0, int y0, int x1, int y1, int r)
//高斯核进行权重划分 边缘锐化效果
//int weight[5][5] = { { 1, 2, 4, 2, 1 }, { 2, 5,6,5, 2 }, { 4, 6, 8,6,4 },{2,5,6,5,2 },{1,2,4,2,1} };
//使用高斯累计核,优化速度
int weight_sum[5][6] = { {0, 1, 3, 7, 9, 10 }, {0, 2, 7,13,18, 20 }, {0, 4, 10, 18,24,28 },{0,2, 7,13,18, 20 },{0,1, 3, 7, 9, 10} };
int weight_1, weight_2, weight_3;
float weight_temp;
int steep = abs(y1 - y0) > abs(x1 - x0);
if (steep)
swap_(x0, y0);
swap_(x1, y1);
if (x0 > x1)
swap_(x0, x1);
swap_(y0, y1);
//compute the slope
float dx = x1 - x0;
float dy = y1 - y0;
float gradient = dy / dx;
if (dx == 0.0f)
gradient = 1;
int xpxl1 = x0;
int xpxl2 = x1;
float intersectY = y0;
int i, j, x;
float temp;
//上边界方程 y-y0 = k*(x -x0)
//下边界方程 y-y0 = k*(x -x0)-r
//因0<K<1 每条边界线只存在两种情况需要透明度计算
//1.穿过一个像素
//2.穿过两个像素
//由此可知R+2为最大像素宽度,不需要抗锯齿的像素位置为 (Y-R +1) < int(Y) < (Y + 1 -2)
//则边界线之间的距离小于3,则还会存在同时穿过一个像素
// main loop
if (steep)
for (x = xpxl1; x <= xpxl2; x++)
weight_1 = 0;weight_2 = 0;weight_3 = 0;
weight_temp = intersectY;
for (j = 0; j < 5; j++)
//上边界经过的像素点
weight_temp += gradient / 5;
temp = fabs(weight_temp - ipart_(intersectY)) * 5;
if (temp > 5.0f)
weight_2 += weight_sum[j][ipart_(temp - 5.0f)];
weight_1 += weight_sum[j][5]; //当穿越时,下面的像素应该是满强度的
//下边界经过的像素点 由直线的对称性得出
weight_3 += weight_sum[j][0];
weight_1 += weight_sum[j][ipart_(temp)];
//下边界经过的像素点 由直线的对称性得出
weight_3 += weight_sum[j][ipart_(5.0f - temp)];
// pixel coverage is determined by fractional
// part of y co-ordinate
if (temp > 5.0f)
setPixelAlpha(ipart_(intersectY) + 1, x, (88 - weight_2) / 88.0f);
setPixelAlpha(ipart_(intersectY), x, weight_3 / 88.0f);
setPixelAlpha(ipart_(intersectY) + r, x, weight_1 / 88.0f);
setPixelAlpha(ipart_(intersectY) + r + 1, x, weight_2 / 88.0f);
for (i = 1; i < r; i++)
setPixel(ipart_(intersectY) + i, x);
setPixelAlpha(ipart_(intersectY) + r, x, weight_1 / 88.0f);
setPixelAlpha((ipart_(intersectY)), x, weight_3 / 88.0f);
for (i = 1; i < r; i++)
setPixel(ipart_(intersectY) + i, x);
intersectY += gradient;
for (x = xpxl1; x <= xpxl2; x++)
weight_1 = 0;weight_2 = 0;weight_3 = 0;
weight_temp = intersectY;
for (j = 0; j < 5; j++)
//上边界经过的像素点
weight_temp += gradient / 5;
temp = fabs((weight_temp - ipart_(intersectY)) * 5);
if (temp > 5.0f)
weight_2 += weight_sum[j][ipart_(temp - 5.0f)];
weight_1 += weight_sum[j][5]; //当穿越时,下面的像素应该是满强度的
//下边界经过的像素点 由直线的对称性得出
weight_3 += weight_sum[j][0];
weight_1 += weight_sum[j][ipart_(temp)];
//下边界经过的像素点 由直线的对称性得出
weight_3 += weight_sum[j][ipart_(5.0f - temp)];
// pixel coverage is determined by fractional
// part of y co-ordinate
if (temp > 5.0f)
setPixelAlpha(x, ipart_(intersectY), weight_3 / 88.0f);
setPixelAlpha(x, ipart_(intersectY) + 1, (88 - weight_2) / 88.0f);
setPixelAlpha(x, ipart_(intersectY) + r, weight_1 / 88.0f);
setPixelAlpha(x, ipart_(intersectY) + r + 1, weight_2 / 88.0f);
for (i = 2; i < r; i++)
setPixel(x, ipart_(intersectY) + i);
setPixelAlpha(x, ipart_(intersectY), weight_3 / 88.0f);
setPixelAlpha(x, (ipart_(intersectY)) + r, weight_1 / 88.0f);
for (i = 1; i < r; i++)
setPixel(x, ipart_(intersectY) + i);
