实战内容：

**10*7有风格子寻路问题**

所需环境：pycharm

所需额外包：gym

一、实际效果：

如上图所示，在一个10*7的格子世界中，Agent将从S出发，前往目的地G，在寻找最优路径上，会遇到下方吹来的不同强度的风，下面的数字代表这风力的等级，比如2级风力，会将Agent向上吹2格。想象一下，若没有风，则和我们的迷宫探宝问题类似，加了风之后，Agent需要花更多的力气去寻找最优路径，难度上显然增加了。

状态空间：70个，为0-69

动作空间：上下左右

如上图所示，黑色实线是Agent移动的最优路径，共需要15步，最优策略是“右右右右右右右右右下下下下左左”。

上图是学习曲线，蓝色代表每个完整episode所需步数，红色代表每个完整episilon的总奖励。从图中可以看出，Agent的第一个完整epsilon的探索往往需要很多步，完成一次探险之后，Agent显然加深了对这个原本对他陌生的环境，之后所花的步数显然见笑了很多，为了看得仔细点，缩小刻度值：

可以看出，差不多50个episode之后，跑完完整一个序列素要200步以内，要知道第一次花了6000多步。在800个episode之后，Agent显然找到了最优路径，花了15步到达终点，有些许的“毛刺”是因为Q-learning所用的ε-greedy有很小的概率会执行随机策略，因此步伐会增多，说明此时ε并没有趋近于0，或者还没完全收敛，显然，继续加大episode，ε会趋近于0，那时候Q-learning才会完全收敛。

Note：一般来说，第一次找到终点所花时间是最久的，当一次找到终点后，理论和实践都表明，之后的时间会减少很多，因为TD算法是基于值迭代的算法，在达到终点次数变多以后，很多Q值在变大的同时会越来越趋于Q真值，由于我们的行为策略都含有贪心策略，因此Agent在选择正确路径上会变得更加有方向。

当ε取很小，但是不衰减，那会怎么样？

如上图所示，将ε=0.1，但是和上面不一样，并不去衰减这个值，理论上不符合GLIE条件，因此其无论执行多少episode，都不会收敛，一来，其对值函数的提升无法最大化，二来虽然ε很小，但其终究存在随机策略的成分，即不是确定性策略，因此其收敛的路径不是唯一确定的，可能大部分时候其能找到最优路径，但是有一定概率会多走几步才到终点（因为存在小概率会执行随机策略），稳定性很差。实际上，如上图所示，原本800个episode就可以收敛到最优策略，但是如今看来，其虽然也有出现最优策略，但是也会伴随着出现多走几步的情况，正如理论分析的那样，其虽存在收敛，但结果不稳定，也就是说会出现很多“ 毛刺 ”。

二、Q-learning算法：

环境E：用于对机器人做出的动作进行反馈，反馈当前奖励r（本设计中，规定拿到宝藏才有奖励，落入陷阱获得负奖励，其余无奖励）与下个状态state'。如实际效果中的横向轴与棋盘

动作空间A：一维中['left', 'right']；二维中[‘up’, 'down', 'left', 'right']

奖赏折扣 $\gamma$ ：Q-learning一般使用 $\gamma$ 折扣累计奖赏，利用动态规划，用状态-动作值函数Q做决策， $\gamma$ 是个对每一步奖赏进行衰减的一个0-1之间的常数，我设为0.9

更新步长 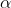$\alpha$ ：也可以说学习率，0-1之间的常数，我设为0.01

尝试概率 $\epsilon$ ：Q-learning会采用 $\epsilon$ -greedy策略去选取动作，0-1之间的值，我设为0.1，也就是10%的概率随机在动作空间A中随机选取动作，90%的概率选取当前最优动作，即aciton* = argmax Q(s,a)

1、初始化动作-状态值函数为pandas表格，index为各个状态，column为动作空间，内容为0；初始化状态s0；随机抽取动作

2、for t=1,2,3...do

3、 r,s' = 在E中执行动作a（a由 $\epsilon$ -greedy策略对当前状态s产生）后产生环境回馈的当前奖励和下个状态。

4、选择最优策略选出s'状态下的动作a'。

5、更新Q表：Q（s，a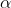） += $\alpha$ * （r + $\gamma$ * Q（s'，a'） - Q（s，a））

6、更新s = s'，输出策略a'' = argmax Q(x, a'')存于Q表中

7、end for

8、最后Q表中的值就是输出的策略policy，通过这个策略，机器人可以以最快速度找到宝藏

note：

1、一维中的状态为x轴点的值0-4，以及宝藏‘end’；二维中为22个点的坐标（x,y）以及陷阱的2个坐标和宝藏‘end’坐标

2、很多Q-learning算法中将4、5两步合并成Q（s，a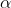） += $\alpha$ * （r + $\gamma$ * max Q（s'） - Q（s，a）），其实是一样的。

3、当s'=宝藏或者陷阱的时候，Q（s'，a'）= 0，因为值函数Q的含义是，在s'状态下，执行a'动作后获得的累积奖励，而找到宝藏和落入陷阱不会执行任何动作，所以没有值。

4、 $\epsilon$ -greedy策略在实际编程过程中，要用的argmax，这个函数在当存在多个值相同时，会选取索引最前面的那个动作，为了避免这个，我们需要在几个相同最大值的动作中进一步随机选取。

5、以一维寻宝为例，第一次尝试成功后，经过努力最终产生一个策略（即Q表），但这个策略并不好用，此时Q中只有拿到宝藏前那个状态_s才有值，而其余均为初始化的0。接下来的尝试中，机器人会向无头苍蝇一样到处乱走，花很久才收敛，第二次尝试成功后，走到 _s前的那个状态__s也会有一个合理的值，其实在__s状态下，由于_s的max特点，会诱导机器人走向_s，而不是往另一个方向走，从而走向宝藏，加快了收敛，这样就是为什么越是训练到后面，机器人寻宝速度越快的原因！因此，接下来的尝试中， Q表中的值会由最后一个状态_s出发，一个个计算出Q表中的其他值，加快收敛，最终形成policy。

6、实际中会发现，在找到最佳策略policy后，机器人偶尔也会“走下弯路”，就是说会比最佳策略还要收敛慢一点。那是因为机器人不完全是按使Q表最大下的最优动作执行的，这是因为 $\epsilon$ -greedy策略有10%会随机选取动作。

7、实际中，需要在状态更新后加点延迟，这样看起来才有效果，不然飞速的执行，人的眼球跟不上的。。。

8、关于第五行Q值的更新原理：Q-learning是基于值迭代算法的，因此r + $\gamma$ * Q（s'，a'）表示target Q，即目标Q值，因此Q-learning算法就需要让下时刻的Q（s,a）无线靠近它，因此采用了一种类似梯度下降的算法，让Q（s,a）每次一小步（步伐取决于学习率lr）不断靠近target Q，最后达到收敛。

三、学习率的影响：

学习率α是当前状态动作对的Q值以一定步伐靠近下个状态动作Q值与到达下个环境后所受的奖励R，即 Q（s，a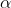） += $\alpha$ * （r + $\gamma$ * Q（s'，a'） - Q（s，a））。 r + $\gamma$ * Q（s'，a'）其实是Gt的替代品，实际也是个估计值，并不准确，因此r + $\gamma$ * Q（s'，a'）的样本均值是Q(s,a)d的有偏估计，但随着一个个episode出现后，r + $\gamma$ * Q（s'，a'）值逐渐接近Gt，最终将无限接近Gt，正在达到取代Gt的位置，那个时候r + $\gamma$ * Q（s'，a'）的样本均值才算是Q(s,a)的无偏差估计，而由于Q-learning这种TD算法的方差很小，因此Q(s,a)的实际值通过软更新的方式无限接近Q(s,a)的真值，最后逐渐稳定下来。这个时候的Q(s,a)对于Gt算得上有比较准确的估计了。

对于α，显然α较大的话，对于收敛速度的还是有提升的，因为Q(s,a)靠近r + $\gamma$ * Q（s'，a'）的步子迈大了。

我们来看看学习率α对有风格子寻路的影响：

α=0.9：

α=0.5：

α=0.1：

从上图可以看出，学习率主要影响到达最优策略的episode长短，学习率越高，到达最优策略越快，反之，则越慢。

但对于第一步的影响，发现学习率并没有那么重要，采样的3个学习率值对于第一步的范围都不太稳定。

四、不足之处&改进方向：

Q-learning对于状态数很多、且连续状态的RL任务显然不能胜任，一来状态搜寻耗费时间，二来多状态消耗存储空间。在本实验中，我分别采用Q字典和Q表来存储Q值，发现前者平均1000个episode需要1.5s完成，后者需要1min，可见Q字典的存储方式是存储有限状态Q值的最佳方式。

对于状态数很多或连续状态，可采用基于值函数近似的方式去估计Q值，常见的有线性近似和神经网络近似，比如DQN算法等，可以有效解决Q-learning的上述不足之处。

Q-l ear ning 也是采用Q表格的方式存储Q值（状态动作价值），决策部分与Sarsa是一样的，采用ε-greedy方式增加探索。 Q-l ear ning 跟Sarsa不一样的地方是更新Q表格的方式。 Sarsa是on-policy的更新方式，先做出动作再更新。 Q-l ear ning 是off-policy的更新方式，更新l ear n()时无需获取下一步实际做出的动作next_action，并假设下一步动作是取最大Q值的动作。 Q-l ear ning 的更新公式：如下图所示，实习的时候，接触到了使用 强化学习 去解决tsp的问题，开始先读了ATTENTION, L EAR N TO SOLVE ROUTING PROBLEMS! 这篇文章，文章里更改了Transformer Architecture，并搭载了 强化学习 中的greedy rollout baseline去解决tsp的问题。无奈背景知识太少，也没有接触过 强化学习 相关的知识，读起来很费劲。经过请教公司的前辈，制定了下... 下面仅对Q-L ear ning 算法对简单介绍Q学习是一种异策略（off-policy）算法。目标策略（target policy）和行为策略（behavior policy）。目标策略就是我们需要去学习的策略，相当于后方指挥的军师，它不需要直接与环境进行交互行为策略是探索环境的策略，负责与环境交互，然后将采集的轨迹数据送给目标策略进行学习，而且为送给目标策略的数据中不需要at+1a_{t+1}at+1，而Sarsa是要有at+1a_{t+1}at+1的。 强化学习 是 机器学习 中的一种重要类型，一个其中特工通过执行操作并查看查询查询结果来学习如何在环境中表现行为。 机器学习 算法可以分为3种：有监督学习（Supervised L ear ning ）、无监督学习（Unsupervised L ear ning ）和 强化学习 （Reinforcement L ear ning ），如下图所示：有监督学习、无监督学习、 强化学习 具有不同的特点：有监督学习是有一个label（标记）的，这个label告诉算法什么样的输入对应着什么样的输出，常见的算法是分类、回归等；相信大多数小伙伴应该和我一样，之前在学习 强化学习 的时候，一直用的是 Python ，但奈何只会用java写后端，对 Python 的一些后端框架还不太熟悉，（以后要集成到网站上就惨了），于是就想用Java实现一下 强化学习 中的Q-L ear ning 算法，来搜索求解人工智能领域较热门的问题—迷宫寻路问题。（避免以后要用的时候来不及写）。下面仅对Q-L ear ning 算法对简单介绍Q学习是一种异策略（off-policy）算法。目标策略（target policy）和行为策略（behavior policy）。那个客户转移到了Akamai，结果在第二天又被同一个DDoS攻击成功，而这间记录非常良好的公司就只有被DDoS攻击成功过一次，因为他们有非常好的分布式架构。此外，对于现行的基于边界网络的防护措施，如果想要利用云计算解决DDOS攻击，利用服务提供商的DDoS基础架构或部署在受害者基础架构上游的专用DDoS攻击防护措施，这些做法都还有很大的差距。现在，最主要的都是应用层的DDoS攻击，它可以不停地耗掉后端服务器，最终用完所有的云计算额度，结果受害者只能选择额外掏钱将云计算的配额加大，或者直接让整个服务关闭。.. Datawhale干货作者：知乎King James，伦敦国王大学知乎｜https://www.zhihu.com/people/xu-xiu-jian-33前言：上篇介绍了什么是... CSS网格布局引入了二维网格布局系统，可用于布局页面主要的区域布局或小型组件。本文介绍了CSS网格布局与CSS网格布局规范 Level 1 中的新术语。 CSS网格布局和弹性盒布局的主要区别在于弹性盒布局是为一维布局服务的（沿横向或纵向的），而网格布局是为二维布局服务的（同时沿着横向和纵向）。这两个规格有一些相同的特性。如果你已经掌握如何使用弹性盒布局的话，你可能会想知道这些相似之处怎样在能... MAZE_H = 4 # grid height 网格高度 MAZE_W = 4 # grid width 网格宽度 class Maze(tk.Tk, object): # 继承 def __init__(self): super(Maze, self).. 在基础阶段我们已经学习了，了解了的概念。Q-L ear ning 的思想就是根据值迭代得到的。但要前面的值迭代每次都对所有状态和动作的Q值更新一遍，这在现实中可行性并不高。Q-L ear ning 只使用进行操作。那么，怎么处理？Q L ear ning 提出了一种更新Q值（在某个时刻在状态s下采取动作a的长期回报。）的办法：上面的公式含义就是：现在的Q值=原来的Q值+学习率*（立即回报+Lambda*后继状态的最大Q值-）我们分析以上公式可知，为了得到最优策略Policy，。那么这种“”怎么实现呢？