一. 单选题（共3题，11.4分）

  R1：IF E1 THEN  （500, 0.01） H1
  R2：IF E2 THEN  （1, 100） H1
  R3：IF E3 THEN  （1000, 1） H2
  R4：IF H1 THEN  （20, 1） H2
且已知P(H1)=0.1，P(H2)=0.1，P(H3)=0.1 
初始证据的概率为P(E1|S1)=0.5，P(E2|S2)=0，P(E3|S3)=0.8。 
用主观贝叶斯的方法求H2的后验概率P(H2|S1,S2,S3)。 
正确答案：
 
解：由已知知识得到的推理网络如图所示： 
25. (简答题)
 
设有如下推理规则 r1: IF E1 THEN (2, 0.0001) H1 
              r2: IF  E1 AND  E2 THEN (100, 0.001) H1
              r3: IF  H1  THEN  (200, 0.01) H2
已知：P(E1)=P(E2)=0.6，P(H1)=0.091，P(H2)=0.01 
用户回答: P(E1|S1)=0.76, P(E2|S2)=0.68 
求：P(H2|S1, S2)的值。 
正确答案：
 
解：由已知知识得到的推理网络如图所示：
  
26. (简答题)
 
设有三个独立的结论H1、H2、H3及两个独立的证据E1、E2，它们的先验概率和条件概率分别为： 
P(H1)=0.4, P(H2)=0.3, P(H3)=0.3, 
P(E1|H1)=0.5, P(E1|H2)=0.3, P(E1|H3)=0.5, 
P(E2|H1)=0.7, P(E2|H2)=0.9, P(E2|H3)=0.1, 
试用概率方法分别求出： 
（1）当只有证据E1出现时的P(H1|E1)、P(H2|E1)、P(H3|E1)值，并说明E1的出现对结论H1、H2、H3的影响； 
（2）当证据E1、E2同时出现时的P(H1|E1,E2)、P(H2|E1,E2)、P(H3|E1,E2)值，并说明E1、E2同时出现对结论H1、H2、H3的影响。 
正确答案：
 
答案解析：（1）0.454；0.205；0.341；（2）0.59；0.34；0.06
				贝叶斯公式贝叶斯公式是机器学习中的基础公式，也是概率统计里的常用公式，贝叶斯公式常用于监督学习算法中的生成（式）模型（Generative Model），想要对机器学习算法建立体系化的知识结构，对生成模型的理解至关重要，本篇只简述贝叶斯公式。并对先验概率和后验概率的知识点进行整理，以便随时查阅。首先给出两个例子 
第一个例子。一所学校里面有 60% 的男生，40% 的女生。男生总是穿长裤，女生则一半
1、人类智能的特征包括（          ）。感知能力、记忆与思维能力、学习能、行为能力
2、人工智能中通常把（             ）作为衡量机器智能的准则。图灵测试
3、人工智能研究的基本内容包括（                 ）。 机器行为、机器感知、机器思维、机器学习
4、人工智能的目的是让机器能够（               ），以实现某些脑力劳动的机械化。模拟、延伸和扩展人的智能
5、李明的父亲是教师，用谓词逻辑可以表示为Teacher（father（Liming））.
				1，什么是朴素贝叶斯算法？
贝叶斯方法是以贝叶斯原理为基础，使用概率统计的知识对样本数据集进行分类。由于其有着坚实的数学基础，贝叶斯分类算法的误判率是很低的。贝叶斯方法的特点是结合先验概率和后验概率，即避免了只使用先验概率的主观偏见，也避免了单独使用样本信息的过拟合现象。贝叶斯分类算法在数据集较大的情况下表现出较高的准确率，同时算法本身也比较简单。
1 . 贝叶斯网络
根据图所给出的贝叶斯网络，其中：P(A)=0.5，P(B|A)=1， P(B|¬A)=0.5， P(C|A)=1， P(C|¬A)=0.5，P(D|BC)=1，P(D|B, ¬C)=0.5，P(D|¬B,C)=0.5，P(D|¬B, ¬C)=0。试计算下列概率P(A|D)。
Answer：
2.概率推理
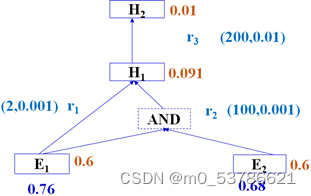
设有如下推理规则
   r1: IF E1 THEN (2, 0.00001) H1
   r2: IF E2 THEN (100, 0.0001).
　　以前在许学习贝叶斯方法的时候一直不得要领,什么先验概率,什么后验概率,完全是跟想象脱节的东西,今天在听喜马拉雅的音频的时候突然领悟到,贝叶斯老人家当时想到这么一种理论前提可能也是基于一种人的直觉.
先验概率:是指根据以往经验和分析得到的概率.[1]
　　意思是说我们人有一个常识,比如骰子,我们都知道概率是1/6,而且无数次重复实验也表明是这个数,这是一种我们人的常识,也是我...
				文章目录一. 基本概念二. 必背公式1. 证据不确定性的组合算法2. 结论不确定性的传递算法3. 结论不确定性的合成算法三. 典型例题例题1例题2四. 通用解法
一. 基本概念
要掌握C-F模型首先需要了解可信度的概念，可信度是根据经验对一个事物或现象为真的相信程度，说白了就是有多大把握相信一个事情。由于可信度不可避免地带有较大主观性和经验性，难以把握准确性。C-F模型便是基于可信度表示的不确定性推理的基本方法。
不确定性推理主要有两种不确定性，即关于知识的不确定性和关于证据的不确定性。
C-F模型中关于知