0 🌲写在前面

Python 机器学习实战专题旨在基于Py thon实现机器学习的经典算法，例如线性回归LR、决策树DT、神经网络、支持向量机SVM等，所有源代码获取方式见文末，如有需要自行下载，🔥欢迎关注作者！

Reference: 周志华老师的《机器学习》西瓜书📖

1 🌲什么是决策树？

决策树(decision tree, DT)模拟人类在面临决策问题时的系列判断处理机制，基于树结构对属性分而治之(divide-and-conquer)学习。

一般地，决策树包含若干分支节点和叶节点，最顶层的分支节点称为根节点。分支节点进行属性划分，叶节点给出分类预测结果。决策树算法的基本形式如表所示。

解释算法中的几个关键点：

决策树算法中递归返回情形(2)用后验分布作为当前叶节点的分布规律；情形(3)则用父节点的先验分布作为当前叶节点的分布规律。

根据 a ∗ = g e t B e s t ( A ) a_*=getBest\left( \boldsymbol{A} \right) a

∗

=getBest(A)策略的构造分为不同子算法。必须指出，若当前节点划分属性为连续属性，则该属性仍可作为子节点划分属性。

暂时看不明白也没关系，下面代码实战的时候会指出每步的过程。

2 🌲常见决策树算法

注： 下面所有算法的公式与西瓜书一致以避免参考不同资料造成的歧义性和不变性。

2.1 👉 ID3算法

ID3决策树算法核心原理是基于信息增益(information gain)筛选最优划分属性：

a ∗ = a r g max ⁡ a ∈ A G a i n ( X , a ) {a_*=\underset{a\in A}{\mathrm{arg}\max}\,\,Gain\left( \boldsymbol{X}, a \right) }

∗

a∈A

argmax

Gain(X,a)

信息增益定义为用属性 a a a对训练集 X X X进行划分后信息熵的减量，或称 X X X样本类别集合纯度的增量：

G a i n ( X , a ) = E n t ( X ) − ∑ v = 1 V ∣ X v ∣ ∣ X ∣ E n t ( X v ) Gain\left( \boldsymbol{X}, a \right) =Ent\left( \boldsymbol{X} \right) -\sum_{v=1}^V{\frac{\left| \boldsymbol{X}^v \right|}{\left| \boldsymbol{X} \right|}Ent\left( \boldsymbol{X}^v \right)}

Gain(X,a)=Ent(X)−

v=1

∑

∣X∣

∣X

∣

Ent(X

)

其中信息熵度量样本集合的类别纯度：

E n t ( X ) = − ∑ k = 1 ∣ Y ∣ p k log ⁡ 2 p k Ent\left( \boldsymbol{X} \right) =-\sum_{k=1}^{\left| \mathcal{Y} \right|}{p_k\log _2p_k}

Ent(X)=−

k=1

∑

∣Y∣

log

接下来的算法实战就是基于ID3算法

2.2 👉 C4.5算法

C4.5决策树算法的核心原理是基于增益率(gain ratio)筛选最优划分属性，相当于对信息增益进行关于属性 a a a粒度——即可取值数目的启发式加权，以避免信息增益偏好可能带来的不利影响：

a ∗ = a r g max ⁡ a ∈ A G a i n _ r a t i o ( X , a ) {a_*=\underset{a\in A}{\mathrm{arg}\max}\,\,Gain\_ratio\left( \boldsymbol{X}, a \right) }

∗

a∈A

argmax

Gain_ratio(X,a)

信息增益率定义为：

G a i n _ r a t i o ( X , a ) = G a i n ( X , a ) I V ( a ) Gain\_ratio\left( \boldsymbol{X}, a \right) =\frac{Gain\left( \boldsymbol{X}, a \right)}{IV\left( a \right)}

Gain_ratio(X,a)=

IV(a)

Gain(X,a)

其中属性固有值(intrinsic value)

I V ( a ) = − ∑ v = 1 V ∣ X v ∣ ∣ X ∣ log ⁡ 2 ∣ X v ∣ ∣ X ∣ IV\left( a \right) =-\sum_{v=1}^V{\frac{\left| \boldsymbol{X}^v \right|}{\left| \boldsymbol{X} \right|}\log _2\frac{\left| \boldsymbol{X}^v \right|}{\left| \boldsymbol{X} \right|}}

IV(a)=−

v=1

∑

∣X∣

∣X

∣

log

∣X∣

∣X

∣

2.3 👉 CART算法

CART决策树算法的核心原理是基于基尼系数(Gini index)筛选最优划分属性

a ∗ = a r g max ⁡ a ∈ A G i n i _ i n d e x ( X , a ) {a_*=\underset{a\in A}{\mathrm{arg}\max}\,\,Gini\_index\left( \boldsymbol{X}, a \right) }

∗

a∈A

argmax

Gini_index(X,a)

基尼系数定义为

G i n i _ i n d e x ( X , a ) = ∑ v = 1 V ∣ X v ∣ ∣ X ∣ G i n i ( X v ) Gini\_index\left( \boldsymbol{X}, a \right) =\sum_{v=1}^V{\frac{\left| \boldsymbol{X}^v \right|}{\left| \boldsymbol{X} \right|}Gini\left( \boldsymbol{X}^v \right)}

Gini_index(X,a)=

v=1

∑

∣X∣

∣X

∣

Gini(X

)

其中基尼值

G i n i ( X v ) = ∑ k = 1 ∣ Y ∣ ∑ k ′ ≠ k p k p k ′ = 1 − ∑ k = 1 ∣ Y ∣ p k 2 Gini\left( \boldsymbol{X}^v \right) =\sum_{k=1}^{\left| \mathcal{Y} \right|}{\sum_{k'\ne k}{p_kp_{k'}}}=1-\sum_{k=1}^{\left| \mathcal{Y} \right|}{p_{k}^{2}}

Gini(X

k=1

∑

∣Y∣

′



∑

′

=1−

k=1

∑

∣Y∣

3 🌲Python实现ID3决策树算法

3.1 🍉 架构设计

主要分为两个模块：决策树生成模块和决策树绘制模块，便于将机器学习算法逻辑和绘制分离，便于维护。

为实现决策树生成模块，可以预定义一般树模块并设计接口，决策树由一般树派生，实现面向接口编程。

树中的节点再定义一个类来封装。

# 树节点
class TreeNode:...
class Tree(ABC):...
# 绘制树
class PlotTree(ABC):...
# 决策树节点
class DTreeNode(TreeNode):...
# 决策树
class DT(Tree):...
# 绘制决策树
class PlotDT(PlotTree):...

3.2 🍉信息熵与信息增益计算

计算信息熵

'''
* @breif: 获得样本集的信息熵 
* @param[in]: data -> 样本集, required: 最后一列为标签列
* @retval: 信息熵
def __getEntory(self, data: DataFrame) -> float:
    ent, label = 0, data.iloc[:, -1]
    for i in list(label.value_counts().index):
        pk = label.value_counts()[i] / label.index.size
        ent = ent - pk * np.log2(pk)
    return ent

计算信息增益

'''
* @breif: ID3决策树划分准则——信息增益
* @param[in]: data -> 样本集, required: 最后一列为标签列
* @param[in]: A -> 样本属性与可取属性值字典
* @retval: 最优划分属性, 连续属性最佳离散分位点(如果该属性是连续属性)
def getAttrByInfoGain(self, data: DataFrame, A: dict):
# 信息增益, 最优划分属性, 连续属性最佳离散分位点
gainInfo, bestA, bestIndex = -9999, None, None
for attr, attrValDict in A.items():
    tempGainInfo = self.__getEntory(data)
    # 若是离散属性
    if not attrValDict['isContinuous']:
        for attrVal in attrValDict['val']:
            subSet = self.__getSubsetByAttr(attr, attrVal, data)
            tempGainInfo = tempGainInfo - self.__getEntory(
                subSet) * subSet.index.size / data.index.size
    # 若是连续属性
    else:...
    if tempGainInfo > gainInfo:
        gainInfo = tempGainInfo
        bestA = attr
        bestIndex = tempBestIndex if attrValDict[
            'isContinuous'] else None
return bestA, bestIndex

为便于展示代码逻辑，未贴出连续属性的情况。

3.3 🍉生成决策树

样本数据集：

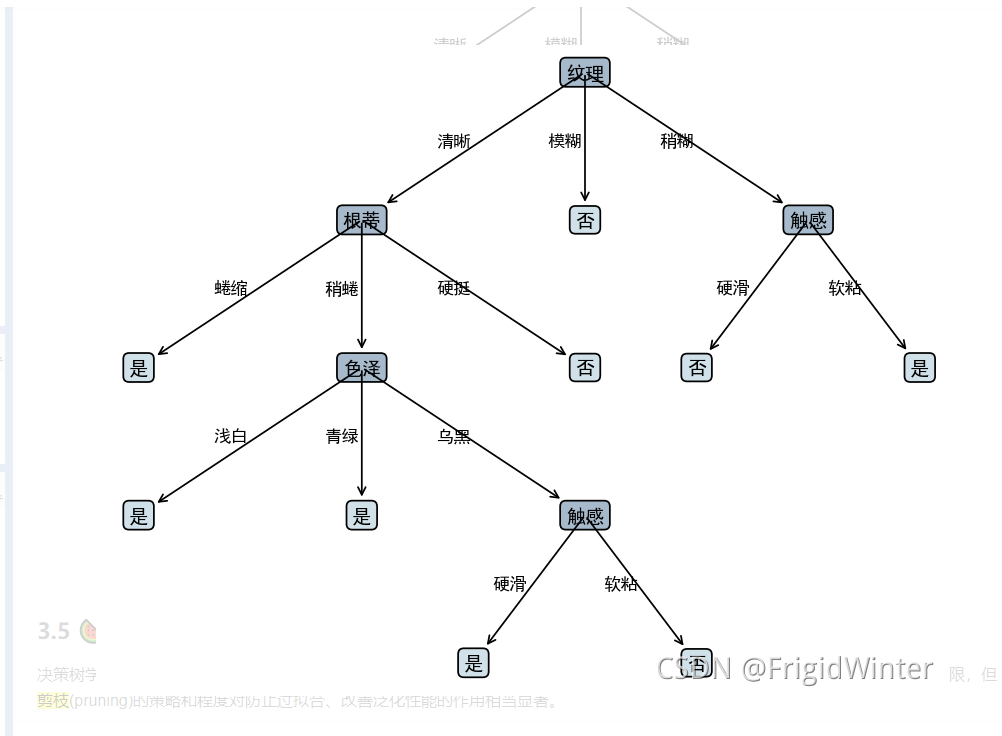
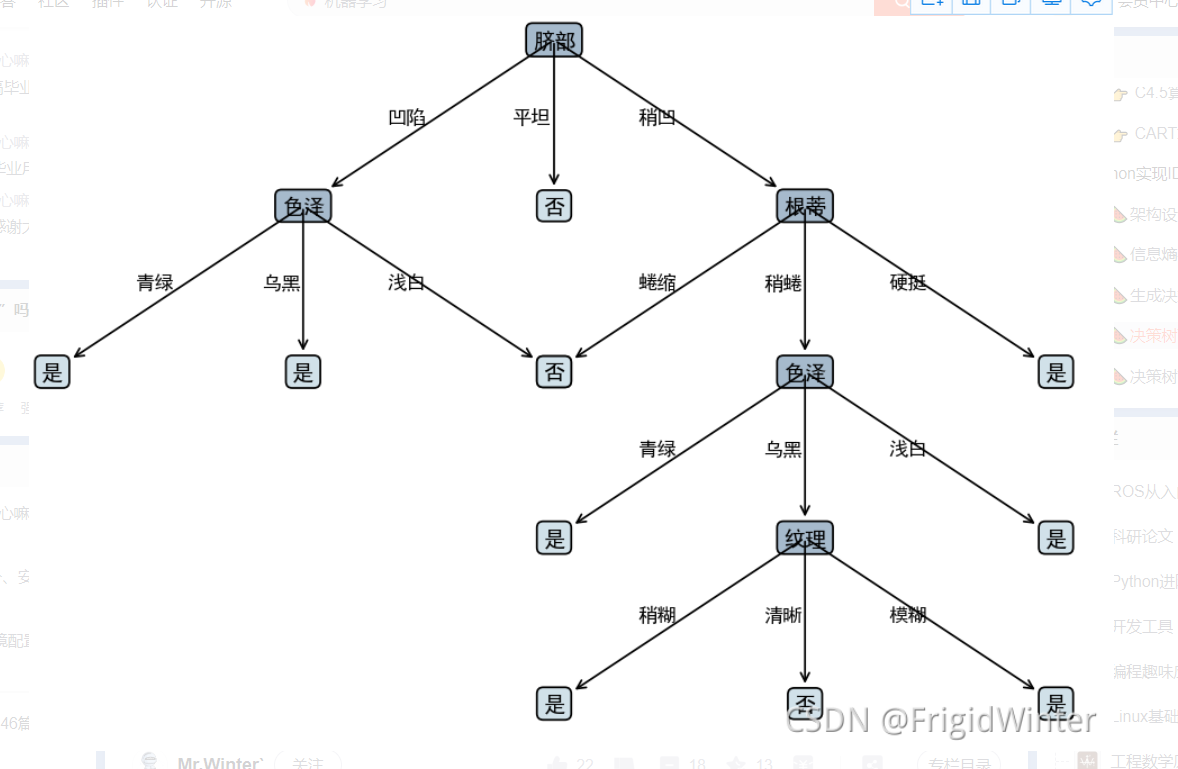
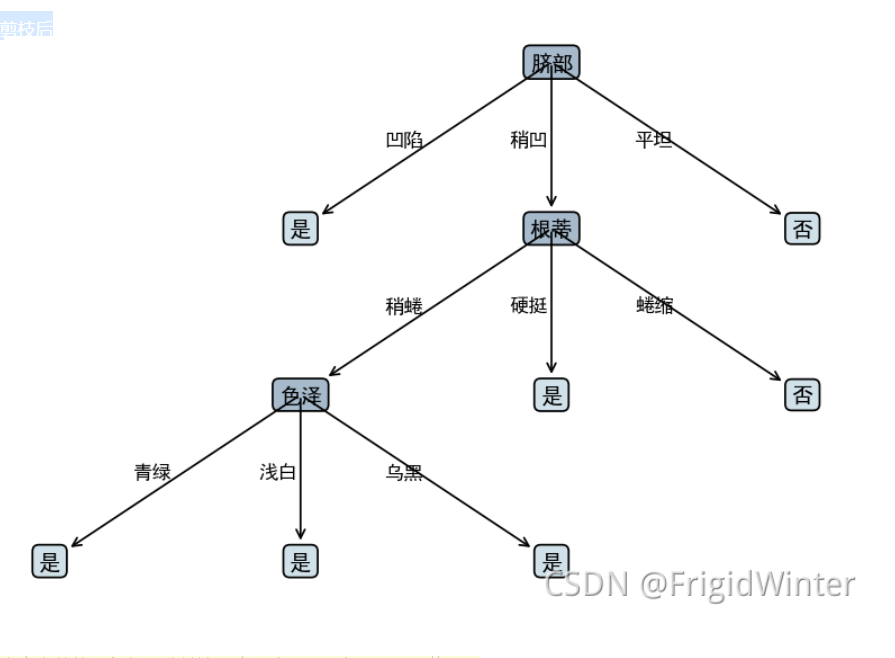
编号,色泽,根蒂,敲声,纹理,脐部,触感,密度,含糖率,好瓜
1,青绿,蜷缩,浊响,清晰,凹陷,硬滑,0.697,0.46,是 
2,乌黑,蜷缩,沉闷,清晰,凹陷,硬滑,0.774,0.376,是 
3,乌黑,蜷缩,浊响,清晰,凹陷,硬滑,0.634,0.264,是 
4,青绿,蜷缩,沉闷,清晰,凹陷,硬滑,0.608,0.318,是 
5,浅白,蜷缩,浊响,清晰,凹陷,硬滑,0.556,0.215,是 
6,青绿,稍蜷,浊响,清晰,稍凹,软粘,0.403,0.237,是 
7,乌黑,稍蜷,浊响,稍糊,稍凹,软粘,0.481,0.149,是 
8,乌黑,稍蜷,浊响,清晰,稍凹,硬滑,0.437,0.211,是 
9,乌黑,稍蜷,沉闷,稍糊,稍凹,硬滑,0.666,0.091,否 
10,青绿,硬挺,清脆,清晰,平坦,软粘,0.243,0.267,否 
11,浅白,硬挺,清脆,模糊,平坦,硬滑,0.245,0.057,否 
12,浅白,蜷缩,浊响,模糊,平坦,软粘,0.343,0.099,否 
13,青绿,稍蜷,浊响,稍糊,凹陷,硬滑,0.639,0.161,否 
14,浅白,稍蜷,沉闷,稍糊,凹陷,硬滑,0.657,0.198,否 
15,乌黑,稍蜷,浊响,清晰,稍凹,软粘,0.36,0.37,否 
16,浅白,蜷缩,浊响,模糊,平坦,硬滑,0.593,0.042,否 
17,青绿,蜷缩,沉闷,稍糊,稍凹,硬滑,0.719,0.103,否

规定样本数据集用dataFrame格式存取，给出生成决策树的接口：

'''
    * @breif: 生成决策树
    * @param[in]: data -> 样本数据集矩阵, required: 最后一列为标签列
    * @param[in]: A -> 样本属性与可取属性值字典
    * @param[in]: depth -> 生成节点的深度
    * @param[in]: func -> 最优属性划分函数
    * @param[in]: parent -> 父节点对象
    * @retval: 完整决策树
    def generateTree(self, data: DataFrame, A: dict, 
    depth: int, func, parent=None):

这里func是函数指针，到时传入信息增益计算函数即可。

按照第一节的算法流程一步步实现：

生成节点：

 # 生成节点
 root = DTreeNode()
 root.parent = parent
 root.depth = depth

递归返回情形

 # 样本全属于同一类别C，则将当前节点标记为C类叶节点
if data.iloc[:, -1].nunique() == 1:
    return root
# A = ∅，则将当前节点标记为样本数最多的类叶节点
if len(A) == 0:
    return root

获得最优划分属性并递归生成

# 获得最优划分属性
root.a, root.isContinuous = func(data, A)
# 遍历最优划分属性的可取属性值
if not root.isContinuous:
    for a in A[root.a]['val']:
        # 获得取值为a的样本子集
        subData = self.__getSubsetByAttr(root.a, a, data)
        if subData.empty:
            child = self.__setChildLeafNode(root, root.label, a)
        else:
            _A = A.copy()
            _A.pop(root.a)  # 移除该属性
            child = self.generateTree(subData, _A, root.depth + 1, func, parent=root)
                    child.aVal = a
                    root.child.append(child)

这里为了不至于混淆，仍没把连续属性的处理粘贴出来，但实际上需要分开处理。

3.4 🍉决策树可视化

决策树可视化的逻辑很简单，这里不赘述，直接看代码，都给出了注释。

class PlotDT(PlotTree):
    def __init__(self, hide=False, graphSize=10) -> None:
        super().__init__(hide=hide, graphSize=graphSize)
    * @breif: 绘制决策树
    * @param[in]: tree -> 决策树根节点
    * @retval: None
    def plotTree(self, tree):
        tree.pos = (0, self.graphSize - 1)  # 指定根节点位置
        self.creatPlot(tree)
        plt.show()
    * @breif: 创建决策树视图
    * @param[in]: tree -> 决策树根节点
    * @retval: None
    def creatPlot(self, tree):
        deltaX, deltaY = 3, 4  # 绘图时节点的X, Y偏置量
        if tree.child:
            num = len(tree.child)
            # 指定子节点起始位置
            startPos = (tree.pos[0] - num // 2 * deltaX,
                        tree.pos[1] - deltaY) if num % 2 == 1 else (
                            tree.pos[0] - (num // 2 - 0.5) * deltaX,
                            tree.pos[1] - deltaY)
            self.__poltNode(tree, tree.a, self.branchNodeStyle)
            for i in range(num):
                tree.child[i].pos = (startPos[0] + i * deltaX, startPos[1])
                self.creatPlot(tree.child[i])
        else:
            self.__poltNode(tree, tree.label, self.leafNodeStyle)
    * @breif: 绘制决策树节点
    * @param[in]: node -> 节点对象
    * @param[in]: nodeText -> 节点文本
    * @param[in]: nodeType -> 节点类型
    * @retval: None
    def __poltNode(self, node, nodeText, nodeType) -> None:
        if node.parent:
            self.plotNode(nodeText, node.pos, node.parent.pos, nodeType)
            midPos = ((node.parent.pos[0] + node.pos[0]) / 2 - 0.5,
                      (node.parent.pos[1] + node.pos[1]) / 2)
            self.plotText(midPos, node.aVal)
        else:
            self.plotNode(nodeText, node.pos, node.pos, nodeType)

3.5 🍉决策树剪枝

决策树学习算法很容易产生过拟合现象，表现为树的尺寸过大且分支过多。不同最优属性划分准则对决策树泛化性能的影响十分有限，但剪枝(pruning)的策略和程度对防止过拟合、改善泛化性能的作用相当显著。

决策树剪枝算法主要分为预剪枝(prepruning)和后剪枝(postpruning)。前者是在决策树生成过程中，划分每个结点前先估计当前结点的划分能否提升泛化性能，若不能则停止划分并将当前结点标记为叶结点；后者是先从训练集生成一棵完整的决策树，然后自底向上遍历分支节点，判决能否提升泛化性能，若不能则将该分支节点标记为叶节点。

在算法实现上主要分为两步：分支节点排序和判断剪枝性能。分支节点按深度排序，从浅到深即为预剪枝，反之为后剪枝。判断剪枝性能即是在验证集上判断精度，剪枝后精度提升就保留剪枝结果，否则不剪。

'''
* @breif: 决策树剪枝
* @param[in]: validData -> 验证集, required: 最后一列为标签列
* @param[in]: ptype -> 剪枝类型 post:后剪枝 pre:预剪枝
* @retval: None
def pruning(self, validData: DataFrame, ptype="post") -> None:
    assert ptype in ('post', 'pre')
    _tree = copy.deepcopy(self.tree)
    branchNodeDict = {i: i.depth for i in self.getBranchNode(_tree)}
    if ptype == "post":
        branchNodeDict = sorted(branchNodeDict.items(), key=lambda x: x[1], reverse=True)
    elif ptype == "pre":
        branchNodeDict = sorted(branchNodeDict.items(), key=lambda x: x[1], reverse=False)
    for _node, depth in branchNodeDict:
        # 剪枝前的预测准确率
        acc = self.calPredictAcc(validData, self.tree)
        # 缓存节点的子代并剪枝
        temp = _node.child
        _node.child = []
        # 剪枝后的预测准确率
        postacc = self.calPredictAcc(validData, _tree)
        if postacc > acc:
            del self.tree
            self.tree = copy.deepcopy(_tree)
        else:
            _node.child = temp

剪枝前

剪枝后

本文完整的工程代码请关注下方公众号，回复“ML002”获取。

🔥 更多精彩专栏 ：

目录

0 🌲写在前面

1 🌲什么是决策树？

2 🌲常见决策树算法

2.1 👉 ID3算法

2.2 👉 C4.5算法

2.3 👉 CART算法

3 🌲Python实现ID3决策树算法

3.1 🍉 架构 设计

3.2 🍉信息熵与信息增益计算

3.3 🍉生成决策树

3.4 🍉决策 树 可视化

3.5 🍉决策树剪枝

3.1 🍉 架构设计

3.4 🍉决策树可视化