R 语言为线性代数的研究提供了矩阵类型,这种数据结构很类似于其它语言中的二维数组,但 R 提供了语言级的矩阵运算支持。
矩阵里的元素可以是数字、符号或数学式。
一个
M x N
的矩阵是一个由
M(row) 行
和
N 列(column)
元素排列成的矩形阵列。
以下是一个由 6 个数字元素构成的 2 行 3 列的矩阵:
R 语言的矩阵可以使用 matrix() 函数来创建,语法格式如下:
matrix(data = NA, nrow = 1, ncol = 1, byrow = FALSE,dimnames = NULL)
参数说明:
data
向量,矩阵的数据
nrow
行数
ncol
列数
byrow
逻辑值,为 FALSE 按列排列,为 TRUE 按行排列
dimname
设置行和列的名称
# Ebyrow 为 FALSE 元素按列排列
N
<-
matrix
(
c
(
3
:
14
)
,
nrow
=
4
, byrow
=
FALSE
)
print
(
N
)
# 定义行和列的名称
rownames
=
c
(
"row1"
,
"row2"
,
"row3"
,
"row4"
)
colnames
=
c
(
"col1"
,
"col2"
,
"col3"
)
P
<-
matrix
(
c
(
3
:
14
)
,
nrow
=
4
, byrow
=
TRUE,
dimnames
=
list
(
rownames
,
colnames
)
)
print
(
P
)
执行以上代码输出结果为:
[,1] [,2] [,3]
[1,] 3 4 5
[2,] 6 7 8
[3,] 9 10 11
[4,] 12 13 14
[,1] [,2] [,3]
[1,] 3 7 11
[2,] 4 8 12
[3,] 5 9 13
[4,] 6 10 14
col1 col2 col3
row1 3 4 5
row2 6 7 8
row3 9 10 11
row4 12 13 14
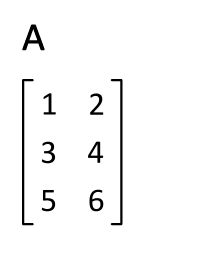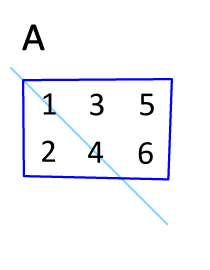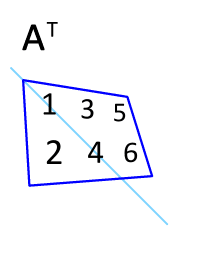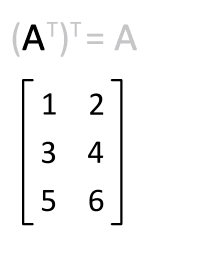
R 语言矩阵提供了
t()
函数,可以实现矩阵的行列互换。
例如有个 m 行 n 列的矩阵,使用 t() 函数就能转换为 n 行 m 列的矩阵。
# 创建一个 2 行 3 列的矩阵
M
=
matrix
(
c
(
2
,
6
,
5
,
1
,
10
,
4
)
,
nrow
=
2
,
ncol
=
3
,byrow
=
TRUE
)
print
(
M
)
[
,
1
]
[
,
2
]
[
,
3
]
[
1
,
]
2
6
5
[
2
,
]
1
10
4
# 转换为 3 行 2 列的矩阵
print
(
t
(
M
)
)
执行以上代码输出结果为:
[,1] [,2] [,3]
[1,] 2 6 5
[2,] 1 10 4
[1] "-----转换-----"
[,1] [,2]
[1,] 2 1
[2,] 6 10
[3,] 5 4
访问矩阵元素
如果想获取矩阵元素,可以通过使用元素的列索引和行索引,类似坐标形式。
# 定义行和列的名称
rownames
=
c
(
"row1"
,
"row2"
,
"row3"
,
"row4"
)
colnames
=
c
(
"col1"
,
"col2"
,
"col3"
)
# 创建矩阵
P
<-
matrix
(
c
(
3
:
14
)
,
nrow
=
4
, byrow
=
TRUE,
dimnames
=
list
(
rownames
,
colnames
)
)
print
(
P
)
# 获取第一行第三列的元素
print
(
P
[
1
,
3
]
)
# 获取第四行第二列的元素
print
(
P
[
4
,
2
]
)
# 获取第二行
print
(
P
[
2
,
]
)
# 获取第三列
print
(
P
[
,
3
]
)
执行以上代码输出结果为:
col1 col2 col3
row1 3 4 5
row2 6 7 8
row3 9 10 11
row4 12 13 14
[1] 5
[1] 13
col1 col2 col3
6 7 8
row1 row2 row3 row4
5 8 11 14
大小相同(行数列数都相同)的矩阵之间可以相互加减,具体是对每个位置上的元素做加减法。矩阵的乘法则较为复杂。两个矩阵可以相乘,当且仅当第一个矩阵的列数等于第二个矩阵的行数。
矩阵加减法
# 创建 2 行 3 列的矩阵
matrix1
<-
matrix
(
c
(
7
,
9
,
-
1
,
4
,
2
,
3
)
,
nrow
=
2
)
print
(
matrix1
)
matrix2
<-
matrix
(
c
(
6
,
1
,
0
,
9
,
3
,
2
)
,
nrow
=
2
)
print
(
matrix2
)
# 两个矩阵相加
result
<-
matrix1
+
matrix2
cat
(
"相加结果:"
,
"
\n
"
)
print
(
result
)
# 两个矩阵相减
result
<-
matrix1
-
matrix2
cat
(
"相减结果:"
,
"
\n
"
)
print
(
result
)
执行以上代码输出结果为:
[,1] [,2] [,3]
[1,] 7 -1 2
[2,] 9 4 3
[,1] [,2] [,3]
[1,] 6 0 3
[2,] 1 9 2
相加结果:
[,1] [,2] [,3]
[1,] 13 -1 5
[2,] 10 13 5
相减结果:
[,1] [,2] [,3]
[1,] 1 -1 -1
[2,] 8 -5 1
矩阵乘除法
# 创建 2 行 3 列的矩阵
matrix1
<-
matrix
(
c
(
7
,
9
,
-
1
,
4
,
2
,
3
)
,
nrow
=
2
)
print
(
matrix1
)
matrix2
<-
matrix
(
c
(
6
,
1
,
0
,
9
,
3
,
2
)
,
nrow
=
2
)
print
(
matrix2
)
# 两个矩阵相乘
result
<-
matrix1
*
matrix2
cat
(
"相乘结果:"
,
"
\n
"
)
print
(
result
)
# 两个矩阵相除
result
<-
matrix1
/
matrix2
cat
(
"相除结果:"
,
"
\n
"
)
print
(
result
)
执行以上代码输出结果为:
[,1] [,2] [,3]
[1,] 7 -1 2
[2,] 9 4 3
[,1] [,2] [,3]
[1,] 6 0 3
[2,] 1 9 2
相乘结果:
[,1] [,2] [,3]
[1,] 42 0 6
[2,] 9 36 6
相除结果:
[,1] [,2] [,3]
[1,] 1.166667 -Inf 0.6666667
[2,] 9.000000 0.4444444 1.5000000
