相关文章推荐
|
|
豁达的熊猫 · 一篇认真的正则入门文章:正则表达式数字和数字 ...· 9 月前 · |
|
|
稳重的刺猬 · [Python技巧]如何加快循环操作和Num ...· 11 月前 · |
|
|
宽容的莲藕 · jquery ...· 1 年前 · |
|
|
小胡子的石榴 · 如何使用Antd的Tabs组件进行样式的设置 ...· 1 年前 · |
|
|
从未表白的遥控器 · c++ - "unknown ca" ...· 1 年前 · |
准备计算机保研面试题
- 大家都是 第一次 ~~~ 没有保研经验,所以担心会被问专业课知识相关的东西。但是结合博主自己的经历,本人双非保到某985,过程中问的最多的是 项目相关问题 ,并不会设计太多专业课问题,问的话也是很简单的 基础知识点 。所以大家专业课准备基础的问题就可以!! 一定要多看项目相关的问题和细节!!!
-
本文涉及学科有操作系统,计算机网络,数据结构,计算机组成,线性代数,高数,概率论与数理统计,机器学习,离散数学…因为懒得加链接,所以dalao们直接
ctrl + f搜索关键字跳转吧~ - 文章很多问题整理于其他博主,因为时间久忘记出处,如果有侵犯请原博主联系我修正更改。希望大家都能去到自己理想的学校~ 本文仅供参考
- 附个人面试真题
-
(1) 什么是曼哈顿距离,什么是欧氏距离,这两者有什么区别?
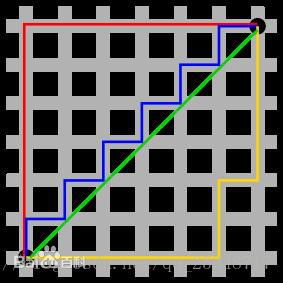
红色的为 曼哈顿距离, 绿色的 为欧氏距离,蓝色和黄色为等价的曼哈顿距离- 马氏距离的目的就是把方差归一化,使得特征之间的关系更加符合实际情况
-
(1)你的大创项目的算法是否和其他算法有所比较,性能如何
(2)讲一下深度学习领域目前的热点和难点
(3)讲讲什么是卷积,什么是卷积神经网络
-
机器学习和深度学习的差别联系
-
梯度下降法和牛顿迭代法的算法过程
- 在编译,链接过程中两者用到的库不一样,在运行过程中两者的运行时系统不一样。而后面问题的答案是使用sudo命令去获取,安装,检测,更新模拟器软件
-
有的编程语言要求必须提前将所有源代码 一次性 转换成二进制指令,也就是生成一个可执行程序(Windows 下的 .exe)称为 编译型语言
-
有的编程语言可以 一边执行一边转换 ,需要哪些源代码就转换哪些源代码,不会生成可执行程序称为 解释性语言
编译型语言:
- 优点:编译器一般会有预编译的过程对代码进行优化。因为编译只做一次,运行时不需要编译,所以编译型语言的程序执行效率高。可以脱离语言环境独立运行。
- 缺点:编译之后如果需要修改就需要整个模块重新编译。编译的时候根据对应的运行环境生成机器码,不同的操作系统之间移植就会有问题,需要根据运行的操作系统环境编译不同的可执行文件。
解释型语言
- 优点:有良好的平台兼容性,在任何环境中都可以运行,前提是安装了解释器(虚拟机)。灵活,修改代码的时候直接修改就可以,可以快速部署,不用停机维护。
- 缺点:每次运行的时候都要解释一遍,性能上不如编译型语言。
1、 路由选择协议
-
内部网关协议
-
路由信息协议(RIP)
- 仅和相邻的路由器交换信息
- 一条路径最多只能包含15个路由器
-
开放最短路径优先协议(OSPF)
- 洪泛法向本自治系统中的所有路由器发送信息
-
路由信息协议(RIP)
-
外部网关协议
- 边界网关协议(BGP)
2、运输层是干嘛的
- 传输层向高层用户屏蔽了底层网络核心的细节如(网络拓扑、路由协议),为运行在不同主机上的进程之间提供了逻辑通信
3、能不能直接在应用层把数据交给网络层
4、在浏览器输入URL后的过程
- ① 域名解析把域名解析成IP地址 DNS域名解析系统
- ② 把IP发送到网络供应端,去找相对应的主机服务器
- ③ TCP的三次握手 建立连接 (TCP的三次握手和四次挥手,后续会上传)
- ④ 开始发送请求 取回入口文件
- ⑤ 开始解析入口文件,并取回需要的资源
- ⑥ 进行后续操作
-

5、说下TCP和UDP区别
- 无连接的非可靠传输层协议
- 向上提供一条不可靠的逻辑信道
- 面向报文流
-
TCP
- 面向连接的传输控制协议
- 向上提供一条全双工的可靠逻辑信道
- 面向字节流
-
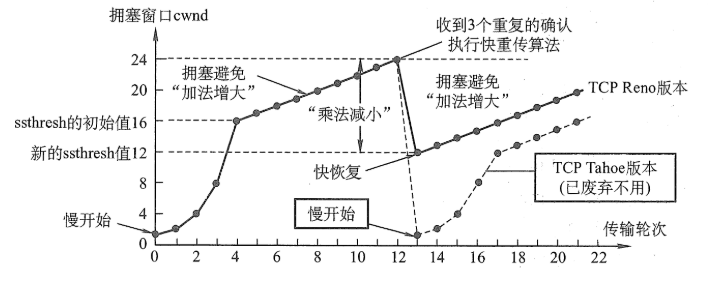
拥塞避免
- 慢开始、拥塞避免、快重传、快恢复
-
6、说下网络中的主机通信流程
- 主机A和主机B在同一个二层网络中,直接走二层交换
- 主机A和主机B不在同一个网络中,走三层路由
7、一个主机将两个端口接到网络上是否会提升吞吐量?为什么?
8、Socket
套 接 字 = ( 主 机 I P 地 址 , 端 口 号 )
- Socket是一组编程接口(API)。介于传输层和应用层,向应用层提供统一的编程接口。应用层不必了解TCP/IP协议细节。直接通过对Socket接口函数的调用完成数据在IP网络的传输。
9、HTTP和HTTPS
- HTTP最初的目的是 为了提供一种发布和接收HTML页面的方法
- HTTPS是HTTP协议的安全版本,HTTP协议的数据传输是明文的,是不安全的,HTTPS使用了SSL/TLS协议进行了加密处理。
- http和https使用连接方式不同,默认端口也不一样,http是80,https是443。
10、三次握手、四次挥手
A C K = 1 , s e q = u + 1 , a c k = w + 1
- 多点接入 , 载波监听 , 碰撞检测
- 记端到端的传播时延为 τ,最先发送的站点最多经过 2τ 就可以知道是否发生了碰撞,称 2τ 为 争用期
12、扩展局域网*
① 在物理层进行扩展
- 使用集线器进行扩展。
② 在链路层进行扩展
- 交换机的问世很快就淘汰了网桥,它实质上是一个多接口网桥,而网桥是两接口。
③ 虚拟局域网
13、地址解析协议(ARP)
- 实现由 IP 地址得到 MAC 地址
- 每个主机都有一个 ARP 高速缓存,里面有本局域网上的各主机和路由器的 IP 地址到硬件地址的映射表。
14、私有地址
- A类:10.0.0.0 - 10.255.255.255
- B类:172.16.0.0 - 172.31.255.255
- C类:192.168.0.0 - 192.168.255.255
1、 快速排序算法,归并排序算法的复杂度
11、CSMA/CD 协议*
推荐文章
