索伯（Sobel）算子原理讲解和实现_中心差分算子和sobel一维算子

1. 简述Sobel算子

索伯算子主要用于边界检测，该算法相对其他的边界检测算法而言是比较的容易。但是对于噪声的鲁棒性要低于其他的边界检测技术。比如canny。
索伯算子是一种多用于边缘检测的离散性差分算子。索伯算子有两组不同的卷积因子，可以为一张图片做横向以及纵向的平面卷积。详细的讲就是，假设要对一张图中的（x，y）这个像素使用索伯算子。首先用两个卷积因子分别对该点做卷积，从而可得出该点在这两个方向上的亮度差分近似值。将xy两个方向的亮度近似值进行结合之后，即可得到该点亮度。得到的是一个数，如果这个值大于了阈值，那么这个点就可以被考虑成边缘点。

2. ndimage.Sobel

首先看看ndimage提供的索伯算子是什么样的效果。要注意的是 python中提供的sobel API，有的只能支出2维的输入，如果不降图片变成灰度图片，直接使用API会出现报错。

ValueError: The parameter `image` must be a 2-dimensional array
sobel算子的实现主要分以下几步来完成。 
 首先需要将需要边缘检测的图像进行黑白处理。因为色彩对于边缘检测的影响很小。
 
 分别计算灰度图片横向和纵向的梯度。
 
 计算两个方向梯度的幅值。
 
 规范化梯度
  
下面以一张彩色的加菲猫照片，来展示简单边缘检测的基本流程个效果。
 代码分成两个板块：边缘检测和图像展示
 边缘检测的代码展示如下： 
def edges_detection(img):
    #img must be grayscaled
    img_gray = sc.rgb2gray(img) 
    #partial derivative of x_axis
    dx = ndimage.sobel(img_gray,1)
    dy = ndimage.sobel(img_gray,0)
    #magnitude
    mag = np.hypot(dx,dy)
    #shown as image. must be 8 bit integer
    # mag = 255.0/ np.amax(mag)
    # mag = mag.astype(np.int8)
    return mag
原图以及图像结果的展示的代码如下所示： 
def plot_res(img,mag):
    figure = plt.figure()
    figure.add_subplot(121)
    plt.imshow(img)
        # plt.show()
    figure.add_subplot(122)
    plt.imshow(mag)
    plt.show()
结果展示如图所示：
  
3. Sobel 算子自实现
 
以下内容为sobel算子python自实现的一些细节。下图是sobel算子实现需要的一些函数
  
convolution函数的是用于对某一个像素点(x,y)进行横向或者纵向的平面卷积。他需要3个参数，x，y，以及x_convolution。x和y顾名思义就是，当前像素的坐标，x_convolution是一个布尔值，如果为正将使用水平方向的卷积因子，反之，则使用纵向的卷积因子。
 convolution 完整代码如下： 
  def convoltiion(self,x,y,x_convolution = True): #calculate single pixel.
        note that all operations must be done within the range.
        Therefore, pay attention on those pixels on the margin.
        operation does not start at(0,0) but (1,1), ends at(x-1,y-1).
        :param x:
        :param y:
        :return:
        y_coordinate = [y-1,y,y+1]
        x_coordinate = [x-1,x,x+1]
        res = 0
        if x_convolution:
            kernel = self.x_kernel
            conv_res = self.x_conv_res
        else:
             kernel = self.y_kernel
             conv_res = self.y_conv_res
        for x_k_cor_ ,x_y in zip(range(kernel.shape[1]),y_coordinate): # y = 0 ,1 2
            for x_k_cor, x_x in zip(range(kernel.shape[0]),x_coordinate): # x = 0,1,2
                res = res + self.gray_img[x_x,x_y] * kernel[x_k_cor,x_k_cor_]
                conv_res[x,y]  = res
        return   conv_res
上述代码的为题在于，循环图中的每一个像素，势必不能保证算法的时间复杂度。因为图片越大，复杂度越大。 
接下来需要将图片中所有的点都用上述的方法，从水平和纵向进分别进行平面卷积，
 两个方向的卷积，原理上没有很大的变化，只是卷积因子发生了改变。 
 def conv(self,Y_):
        for y_coordinate in range(1,img_gray.shape[1]-1):
            for x_coordinate in range(1,img_gray.shape[0]-1):
               res_ =  self.convoltiion(x_coordinate,y_coordinate,x_convolution=Y_)
        return res_
当求得了水平方向和纵向的卷积结果之后，将两个方向的结果结合起来便可以得到赋值。 
    def magnitude(self,x_conv,y_conv):
        return np.sqrt(np.square(x_conv)+np.square(y_conv))
之后显示一下效果： 
 def my_plot(self,x_conv_res,y_conv_res,mag):
        figure_ = plt.figure()
        ax1 = figure_.add_subplot(141)
        ax1.set_title('original img')
        plt.imshow(img_array)
        ax2= figure_.add_subplot(142)
        ax2.set_title('x_convolution')
        plt.imshow(x_conv_res,cmap='gray')
        ax3 = figure_.add_subplot(143)
        ax3.set_title('y_convolution')
        plt.imshow(y_conv_res,cmap='gray')
        ax4 = figure_.add_subplot(144)
        ax4.set_title('magnitude')
        plt.imshow(mag,cmap='gray')
        plt.show()

 实现的效果与ndimage的效果类似。颜色的不同是因为在画图的时候，更改了cmap。 
4. Sobel算子的一些缺陷和替代方案
 
从图中可以看到的是用sobel的边缘检测，检测出来的边界是比较粗的，意味着这样的检测方式在一些情况下是不够精确的，因为我们最理想的状态是边缘的宽度是一很窄的线（单像素），而不是一个区域。在实际的生产中，我们通常会使用canny的边缘检测算法。它的效果相符于前者的效果更好。简单而言，canny对噪音的鲁棒性要比sobel要好。 canny的API在skimage.feature中提供。代码与三者比较如下所示： 
    canny_ = canny(img_gray, sigma=5)
                    文章目录边缘检测边缘检测边缘检测是常用的数字图像处理方法之一。具体的边缘检测方法可以使用sobel(索伯)来做。索伯算子是一种多用于边缘检测的离散性差分算子。索伯算子有两组不同的卷积因子，可以多一张图片做横向以及纵向的平面卷积。详细的讲就是，假设要对一张图中的（x，y）这个点使用索伯算子。首先用两个卷积因子分别对该点做卷积，从而可得出该点在这两个方向上的亮度差分近似值。将xy两个方向的亮度近似值进行结合之后，即可得到该点亮度。 得到的是一个数，如果这个值大于了阈值，那么这个点就可以被考虑成边缘点。
Soble边缘检测算法比较简，实际应用中效率比canny边缘检测效率要高，但是边缘不如Canny检测的准确，但是很多实际应用的场合，sobel边缘却是首选，尤其是对效率要求较高，而对细纹理不太关心的时候。Soble边缘检测通常带有方向性，可以只检测竖直边缘或垂直边缘或都检测。
    算子使用两个3*3的矩阵（图1）算子使用两个3*3的矩阵（图1）去和原始图片作...
				1.拉普拉斯(Laplacian)算子
1.1基础介绍
最简单的各向同性导数算子是拉普赖斯算子，其具有旋转不变性，对于两个变量的函数f(x,y)f(x,y)f(x,y),其定义为
▽2f=∂2f∂x2+∂2f∂y2\triangledown^2f=\frac{\partial ^2f}{\partial x ^2} + \frac{\partial ^2f}{\partial y ^2}▽2f=∂x2∂2f+∂y2∂2f,以离散形式表示上述公式为：
<br/>x方向有：$\frac{\par




    

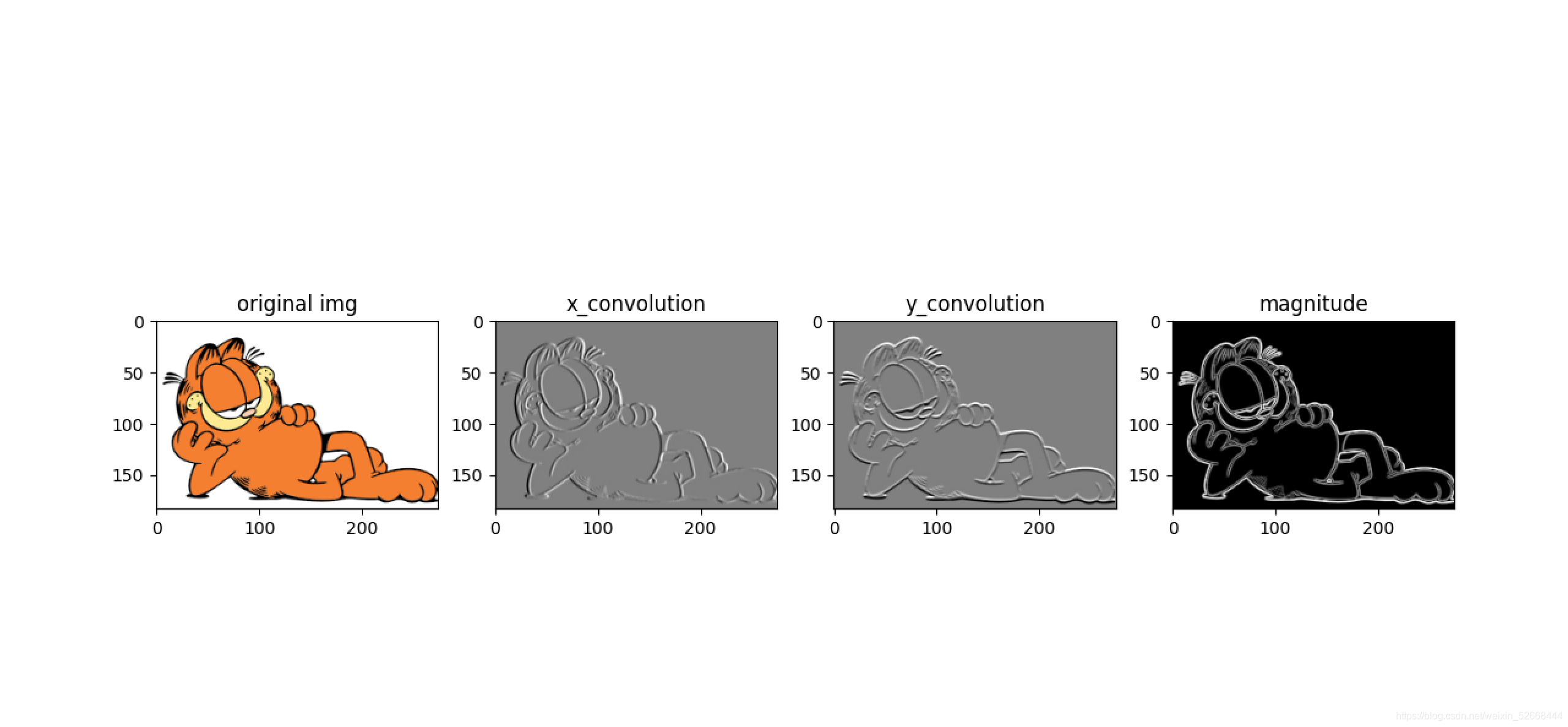
				边缘检测类似微分运算，本质是检测图像的亮度变化。因此，噪声必然会对图像检测结果带来影响。为了避免噪声对检测算子的影响，在构造边缘检测算子的时候不仅需要考虑差分处理，害的考虑平滑处理，这样既能滤除噪声又能检测边缘。类似一阶差分模板，Roberts交叉算子只是考虑了差分因素，而Prewitt他算子通过对一阶差分模板扩展成3*3的尺寸从而引入了均值运算。Sobel算子被认为是较好的检测模板，它考虑差分因素还兼顾了类似高斯平滑的平滑处理。
				索贝尔算子（Sobeloperator）主要用于获得数字图像的一阶梯度，是一种离散性差分算子。它是prewitt算子的改进形式，改进之处在于sobel算子认为，邻域的像素对当前像素产生的影响不是等价的，所以距离不同的像素具有不同的权值，对算子结果产生的影响也不同。一般来说，距离越远，产生的影响越小。
图像处理中认为，灰度值变化剧烈的地方就是边缘。那么如何判断灰度值变化？如何度量“剧烈”？sobel算子就对这些问题做了自己的规范，而且命名为sobel算子，就是对一副图像的输入到输出边缘信息的整...
				索贝尔算子（Sobeloperator）主要用作边缘检测，在技术上，它是一离散性差分算子，用来运算图像亮度函数的灰度之近似值。在图像的任何一点使用此算子，将会产生对应的灰度矢量或是其法矢量
Sobel卷积因子为：
该算子包含两组3x3的矩阵，分别为横向及纵向，将之与图像作平面卷积，即可分别得出横向及纵向的亮度差分近似值。如果以A代表原始图像，Gx及Gy分别代表经横向及纵向边缘检测的图像灰度
				拉普拉斯算子和索伯算子都是图像处理中常用的边缘检测算子，用于检测图像中的边缘和轮廓。
拉普拉斯算子是一种二阶微分算子，它可以通过计算图像中像素点周围像素值的二阶差分来检测边缘。拉普拉斯算子有不同的离散形式，其中最常用的是3x3的离散拉普拉斯算子，其模板如下：
| 0  1  0 |
| 1 -4  1 |
| 0  1  0 |
索伯算子是一种一阶微分算子，它可以通过计算图像中像素点周围像素值的一阶差分来检测边缘。索伯算子有水平和垂直两个方向，其中水平方向的索伯算子模板如下：
| -1  0  1 |
| -2  0  2 |
| -1  0  1 |
垂直方向的索伯算子模板如下：
| -1 -2 -1 |
|  0  0  0 |
|  1  2  1 |
在实际应用中，可以将水平和垂直方向的索伯算子组合起来，形成一个2x2的算子：
| -1  0 |
|  0  1 |
这个算子可以通过卷积运算来应用到图像上，以检测图像中的边缘。