人工智能能不能通过机器学习,预测未来股票走势?
11 个回答
可行,并且, BigQuant 已成功将此项目落地,现已为15000+ 量化投资者和数10家券商/基金/高校等机构提供服务。其中Top5券商中BigQuant已服务3家。
早在10年前,小编的老大,当时还在微软带领团队利用大规模机器学习研发bing搜索引擎的BigQuantCEO梁举,就意识到人工智能今后在投资领域一定会有很大的发展空间,在这10年之中,经过不断的探索实践,最终成功研发出 BigQuant——人工智能量化投资平台 。
小编下面来简单的为大家阐述下人工智能可以给投资带来什么好处,以及为什么这个事情是可行的。对于一位优秀的投资者来说,他获取正收益的关键在于他过去多年积累的丰富投资经验,通过对经验的复用,进而可以对新的未来情形做出有效的决策,而这些“经验”对于机器来说,可以理解为一条条“数据”;人的精力有限,在这个大数据时代下,机器所能获取储备的数据远远要比人多得多,这也就意味着,机器的“经验”要比人丰富的多,普通投资者需要五年甚至十年才能积累到的经验对于机器来说只需短短的几分钟,在短时间内机器可以利用相关算法从历史海量数据中找出潜在规律,产生预测模型,指导投资者进行投资;另一方面,情绪是投资的一大天敌,机器可以很大程度剔除情绪的干扰,客观理性的通过数据进行分析。从过去的经验告诉我们,在大数据时代下,人工智能可以比人做的更好,它可以帮助普通投资者短时间内赶超经验丰富的投资者。
AI应用于金融领域在过去一段时间内确存在一定的争议,主要原因在于相比于楼主提到的围棋Alphago,金融交易是一个更杂乱的环境,外部干扰因素噪音更多,更加依靠于海量的数据集和更强大的计算能力,这些在过去是难以达到的,导致AI与金融迟迟没有交集,即使相结合表现出的效果也差强人意。与过去不同的是,现在新数据集以及足够强大计算机的出现弥补了这一尴尬的问题,金融市场海量标准化数据天然适合人工智能的发展,这也使得人工智能在金融领域终于可以有一片用武之地。
BigQuant 是一家人工智能量化投资平台,也是国内首个将人工智能应用于量化投资领域的平台级产品。为确保AI实现预测股票涨跌结果真实可靠,避免“Garbage In Garbage Out”,平台拥有A股、美股、港股、期货、期权等多市场海量标准化数据,以及有别于传统量化平台的新闻、社交等海量若特征数据,全面支持主流AI框架。平台自主研发出专门应用于股票市场的StockRanker算法,对未来一段时间内的股票进行打分排序,推选出最优投资组合。
BigQuant平台目前90%以上的策略均是人工智能驱动的AI投资策略,用户既可以在平台免费使用人工智能技术开发AI选股策略,也可以选取他人较为成熟的AI策略作为投资参考,大家如果感兴趣可以进一步了解。
01 引言
关于金融时间序列分析,公众号已经发布了系列推文,其中《
【手把手教你】时间序列之日期处理
》展示了如何使用Python处理时间序列日期转换和统计分析;《
【Python量化基础】时间序列的自相关性与平稳性
》介绍了自相关性、偏自相关性、白噪声和平稳性等基础概念和检验过程;《
【手把手教你】使用Python玩转金融时间序列模型
》分享了使用Python构建AR、MA、ARMA和ARIMA等经典时间序列模型。《
Python玩转金融时间序列之ARCH与GARCH模型
》着重介绍了ARCH和GARCH模型的基本原理和分析实例。本文在此基础上,对金融资产收益率进行全方位的可视化分析,为大家更好的理解平稳性概念,揭示为何资产收益率不满足平稳性条件,以及为何机器学习或深度学习在金融资产(如股票)上的预测往往效果不佳提供一个分析视角。
02 数据获取
使用tushare获取股票指数收盘价数据,计算日对数收益率。
#先引入后面可能用到的包(package)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
%matplotlib inline
#正常显示画图时出现的中文和负号
from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False
import tushare as ts
def get_price(code,start,end):
df=ts.get_k_data(code,start,end)
df.index=pd.to_datetime(df.date)
return df.close
codes=['sh','sz','cyb','zxb','hs300']
names=['上证综指','深证综指','创业板指','中小板指','沪深300']
end_day = pd.to_datetime('2020-10-30')
start_day = end_day - 10 * 252 * pd.tseries.offsets.BDay()
start=start_day.strftime('%Y-%m-%d')
end=end_day.strftime('%Y-%m-%d')
#指数收盘价数据
df = pd.DataFrame({name:get_price(code, start, end) for name,code in zip(names,codes)})
(
df/df.iloc[0]-1).plot(figsize=(12,7))
plt.title('指数累计收益率\n2011-2020',size=15)
plt.show()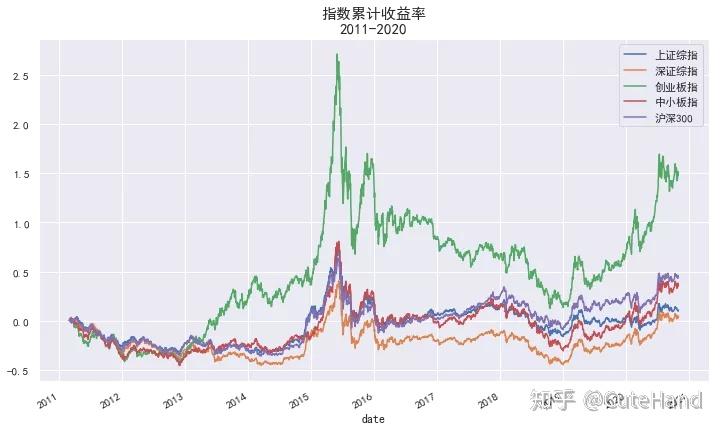
计算股票指数的日对数收益率。实际上在经济金融上,采用对数收益率已经是约定俗成了,当然这样处理主要是基于对数处理的统计特性比较适合建模,如为了使数据更加平滑,克服数据本身的异方差等。
rs=(np.log(df/df.shift(1))).dropna()
rs.plot(figsize=(12,5))
plt.title('指数日对数收益率',size=15)
plt.show()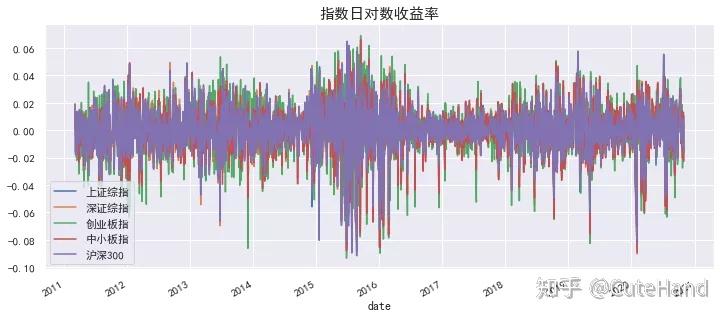
03 收益率平稳性可视化分析
所谓的时间序列平稳性,简单的理解是,序列的均值和方差不应该随着时间的推移而改变。时间序列中收益之间的协方差也不应是时间的函数。
下面将演示和分析在预测时间序列时当数据不满足模型假设条件的挑战。在开始之前,我们要知道,证券收益率序列往往不满足平稳性的要求。
import scipy.stats as stats
def add_mean_std_text(x, **kwargs):
mean, std = x.mean(), x.std()
mean_tx = f"均值: {mean:.4%}\n标准差: {std:.4%}"
txkw = dict(size=14, fontweight='demi', color='red', rotation=0)
ymin, ymax = plt.gca().get_ylim()
plt.text(mean+0.025, 0.8*ymax, mean_tx, **txkw)
return
def plot_dist(rs, ex):
plt.rcParams['font.size'] = 14
g = (rs
.pipe(sns.FacetGrid, height=5,aspect=1.5)
.map(sns.distplot, ex, kde=False, fit=stats.norm,
fit_kws={ 'lw':2.5, 'color':'red','label':'正态分布'})
.map(sns.distplot, ex, kde=False, fit=stats.laplace,
fit_kws={'linestyle':'--','color':'blue', 'lw':2.5, 'label':'拉普拉斯分布'})
.map(sns.distplot, ex, kde=False, fit=stats.johnsonsu,
fit_kws={'linestyle':'-','color':'green','lw':2.5, 'label':'约翰逊分布'})
.map(add_mean_std_text, ex))
g.add_legend()
sns.despine(offset=1)
plt.title(f'{ex}收益率',size=15)
return
plot_dist(rs, '上证综指')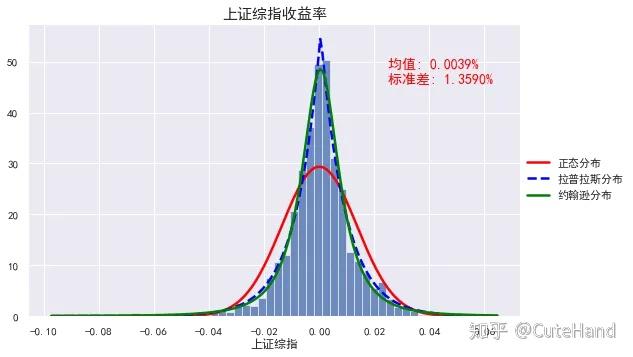
从上图我们可以看出正态分布对数据集的拟合程度是很差,而拉普拉斯分布和约翰逊分布在拟合收益率方面相对较好。统计分布图表明,在样本时间段内,股票指数收益率不是正态分布。
下面进一步用分位数图来比较参数的分位数分布,考察与正态分布的偏离情况。
plt.rcParams['figure.figsize'] = 10,7
def quantile_plot(x, **kwargs):
res = stats.probplot(x, fit=True, plot=plt)
_slope, _int, _r = res[-1]
ax = plt.gca()
ax.get_lines()[0].set_marker('s')
ax.get_lines()[0].set_markerfacecolor('r')
ax.get_lines()[0].set_markersize(13.0)
ax.get_children()[-2].set_fontsize(22.)
txkw = dict(size=14, fontweight='demi', color='r')
r2_tx = "r^2 = {:.2%}\nslope = {:.4f}".format(_r, _slope)
ymin, ymax = ax.get_ylim()
xmin, xmax = ax.get_xlim()
ax.text(0.5*xmax, .8*ymin, r2_tx, **txkw)
return
quantile_plot(rs['上证综指'])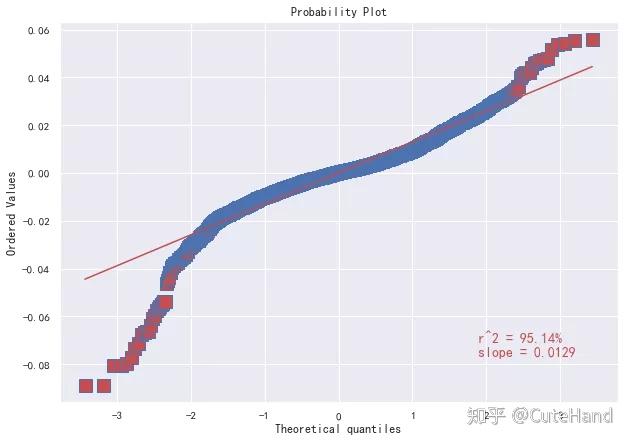
分位数图清晰地显示出,上证综指收益率表现出“肥尾”的现象(概率分布图也可以看出是“尖峰后尾”)。这意味着,极端回报(无论是正回报还是负回报)出现的频率,远远高于正态分布预测的频率。
但是,我们还没有真正进入讨论时间序列平稳性的问题。
检验收益率是否平稳的一种方法是考察每年收益率的均值和标准差的变动情况。如果这两个变量不是时间的函数,那么它们每年的均值应该是非常相似的。
def plot_facet_hist(rs, ex):
plt.rcParams['font.size'] = 12
df = rs.assign(year=lambda df: df.index.year)
g = (sns.FacetGrid(df, col='year',col_wrap=2, height=4, aspect=1.2)
.map(sns.distplot, ex, kde=False, fit=stats.norm,
fit_kws={ 'lw':2.5,'color':'red', 'label':'正态分布'})
.map(sns.distplot, ex, kde=False, fit=stats.laplace,
fit_kws={'linestyle':'--','color':'blue', 'lw':2.5, 'label':'拉普拉斯分布'})
.map(sns.distplot, ex, kde=False, fit=stats.johnsonsu,
fit_kws={'linestyle':'-', 'color':'green','lw':2.5, 'label':'约翰逊分布'})
.map(add_mean_std_text, ex))
g.add_legend()
g.fig.subplots_adjust(hspace=.20)
sns.despine(offset=1)
return
plot_facet_hist(rs, '上证综指')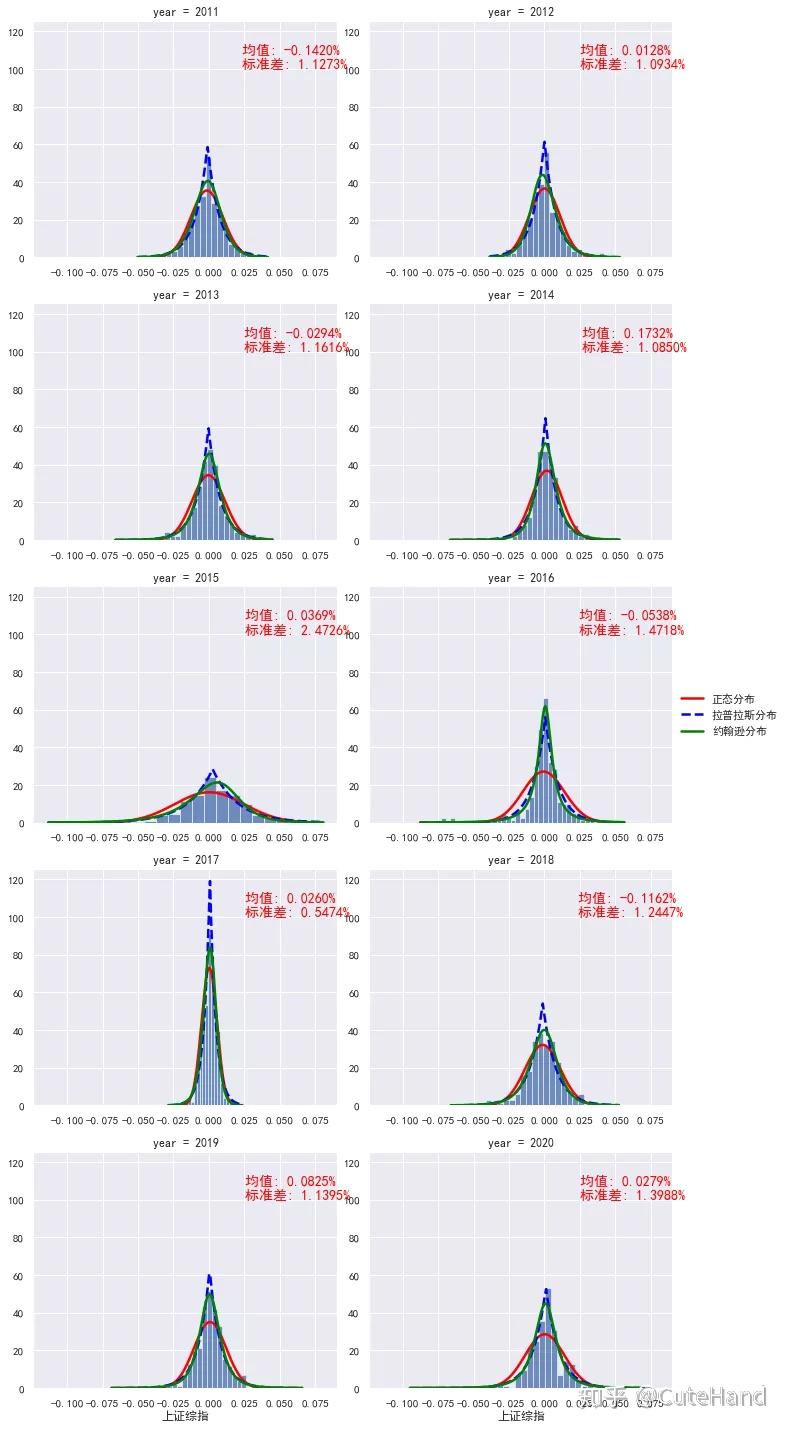
(rs.groupby(rs.index.year)['上证综指']
.agg(['mean', 'std'])
.plot(marker='o', subplots=True))
plt.show()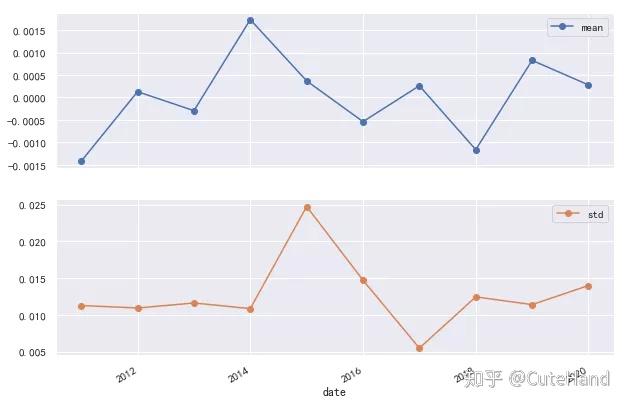
显然,直方图中拟合的正态密度图在每一年中差异很大,某些年份近似服从正态分布,而某些年份表现出较强的“尖峰后尾”。这是否意味着我们之前关于收益率不是正态分布的结论只是一个时间尺度的问题?下面通过分位数图进一步考察这个问题。
def plot_facet_qq(rs, ex):
df = rs.assign(year=lambda df: df.index.year)
g = (df
.pipe(sns.FacetGrid, col='year',col_wrap=2,
height=7,aspect=1.3)
.map(quantile_plot, ex)
.fig.subplots_adjust(hspace=0.2))
sns.despine(offset=1, trim=True)
return
plot_facet_qq(rs, '上证综指')
历年的收益率QQ图也显示出,在某些年份收益率分布近似满足正态分布;而在其他年份,则不满足正态分布。所以可以认为,通过视觉观察,收益率序列的均值和方差是时间的函数,即收益率序列的均值和方差会随着时间的变动而变化。
模拟正态分布样本和累积分布。
norm = stats.norm
RANDOM_STATE=888
def generate_norm_rvs(ser, N=None):
if not N: N = ser.shape[0]
return norm.rvs(ser.mean(), ser.std(), size=N, random_state=RANDOM_STATE)
def generate_norm_pdf(ser, N=None):
if not N: N = ser.shape[0]
_min, _max = ser.min(), ser.max()
x = np.linspace(_min, _max, N)
y = norm.pdf(x, ser.mean(), ser.std())
return x, y
def generate_norm_cdf(ser, N=None):
if not N: N = ser.shape[0]
_min, _max = ser.min(), ser.max()
x = np.linspace(_min, _max, N)
y = norm.cdf(x, ser.mean(), ser.std())
return x, y最后,基于Kolmogorov-Smirnov对收益率分布进行统计检验。
使用收益率的累积分布(CDF),并使用kolmogorov-smirnov的二样本检验(scipy.stats.kstest)与拟合CDF或经验CDF进行比较。该检验可以验证两个样本的CDF是否来自相同的分布,例如正态分布。kstest输出ks统计量和一个p值。p值小于0.05意味着我们可以拒绝两个系列来自同一分布的原假设。p值越小,我们就越确信它们来自不同的分布。
首先,我们将分析整个收益率序列,然后比较各个年份的检验结果。
def plot_cdf(ser, **kwds):
g = sns.kdeplot(ser, cumulative=True, lw=3, color='blue')
x, y = generate_norm_cdf(ser) # 生成正态分布CDF
g.plot(x, y, color='red', lw=3, label='fitted normal CDF')
ks, p = stats.kstest(ser, 'norm', args=(ser.mean(), ser.std()))
xmin,xmax=plt.gca().get_xlim()
ymin,ymax=plt.gca().get_ylim()
txkw = dict(size=14, fontweight='demi', color='red', rotation=0)
tx_N = ser.shape[0]
tx_args = (ks, p, tx_N, ser.shape[0])
tx = 'ks 2 sample test\nks: {:.4f}, p: {:.4f}\nrvs sample N: {:.0f}\nreturn sample N: {:.0f}'.format(*tx_args)
plt.text(xmax*0.2, 0.2*ymax, tx, **txkw)
sns.despine(offset=1)
(plt.legend(frameon=True, prop={'weight':'demi', 'size':12})
.get_frame())
return
plot_cdf(rs['上证综指']) 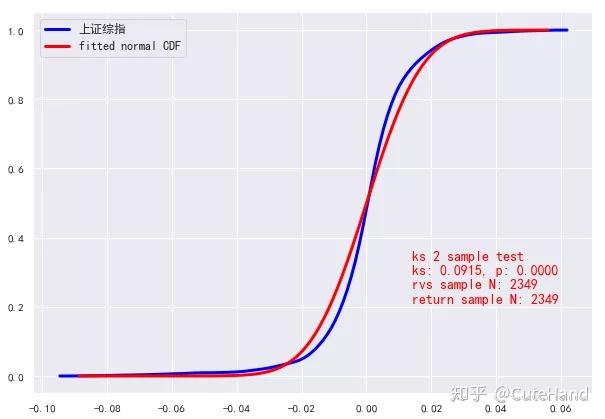
def plot_facet_cdf(rs, ex, **kwds):
df=rs.assign(year=lambda df:df.index.year)
g = (df
.pipe(sns.FacetGrid,
col='year',
col_wrap=2,
height=5,
aspect=1.3)
.map(plot_cdf, ex, **kwds))
g.add_legend()
g.fig.subplots_adjust(hspace=.20)
sns.despine(offset=1)
return
plot_facet_cdf(rs, '上证综指')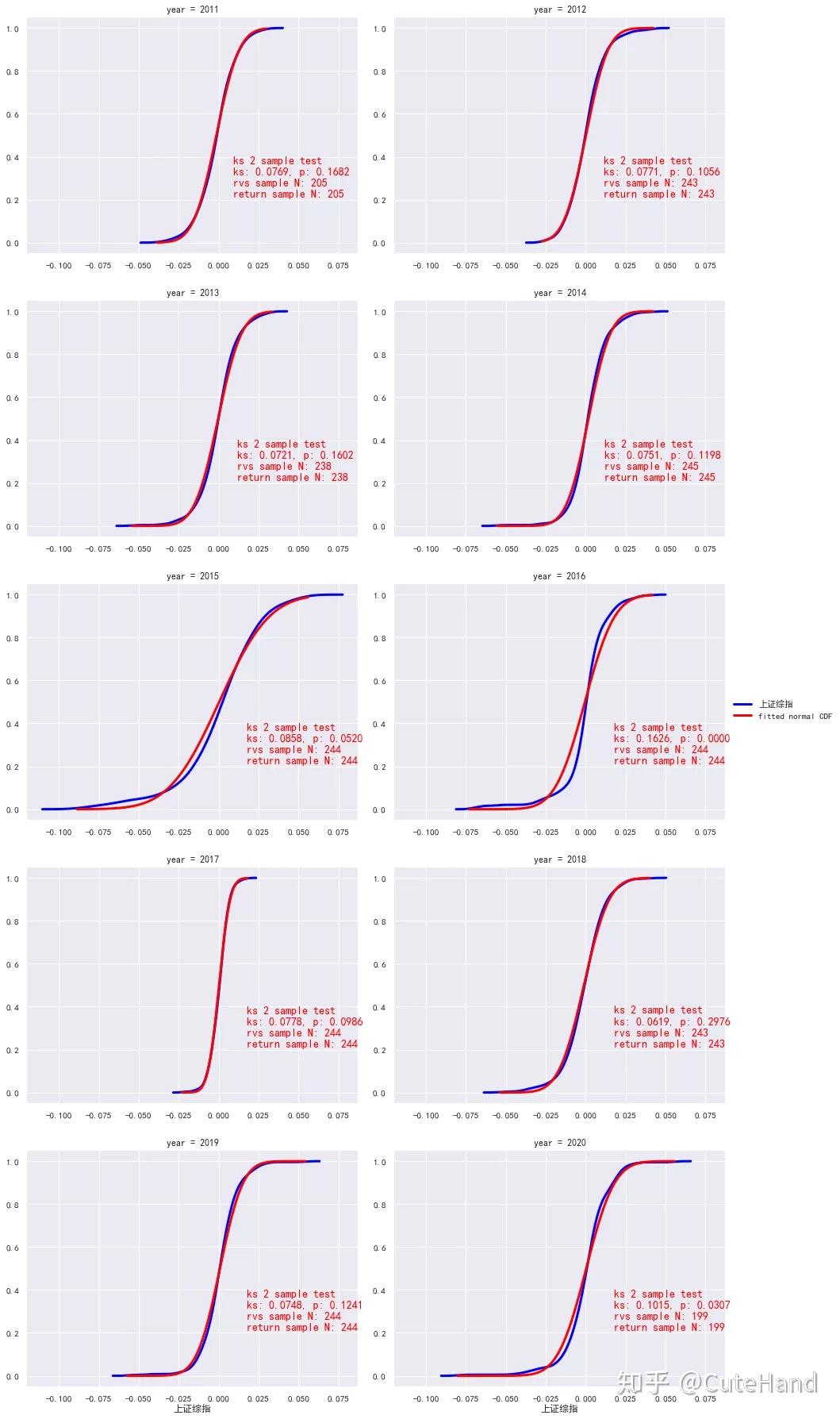
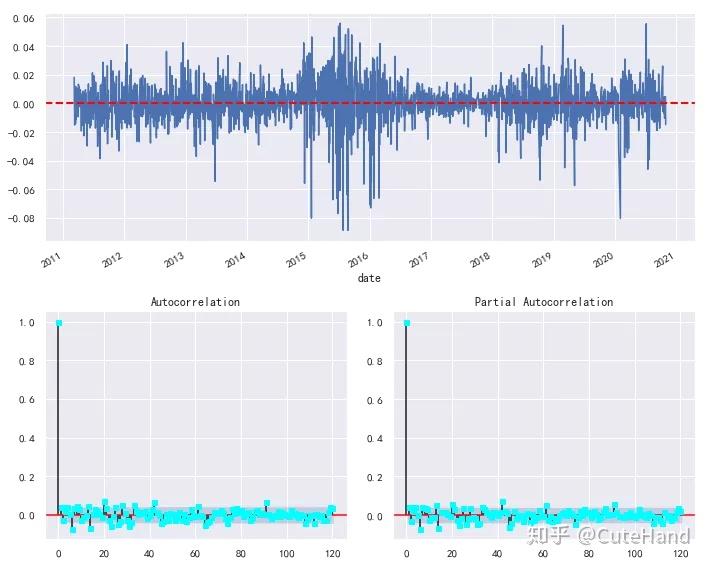
总体收益率的自相关系数和偏相关系数图
关于时间序列的自\偏相关系数图代码可参见《 【Python量化基础】时间序列的自相关性与平稳性 》。
历年日收益率的自相关系数和偏相关系数图
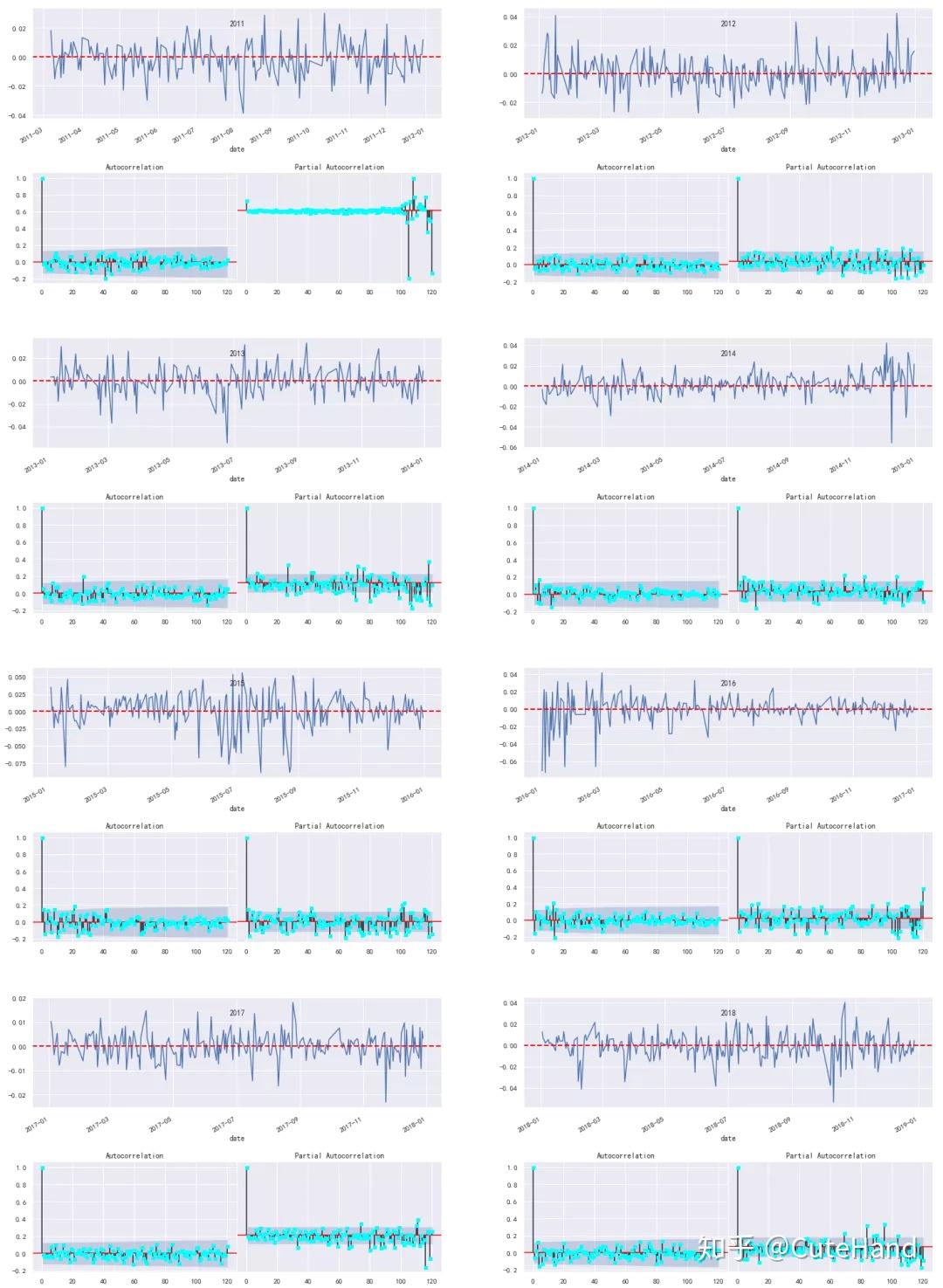
上述图形清晰表明,上证综指收益率在均值和方差上是非平稳的,并且显示了变量自相关的时间段。此外,我们看到上证综指收益率的总体分布非正态分布,但在各种不同的时间期间,如每年,有一段时期是近似正态分布的。那么,当我们试图使用过去的收益率近似于正态分布的统计指标(均值、方差)来预测未来的收益分布时,会出现什么问题呢?
为了探究这个问题,下面使用机器学习包sklearn的 TimeSeriesSplit方法考察样本的分布情况,该方法提供了交叉验证的前向walf-forward形式,使用先前的数据点来序列地预测下一个周期,从而保留了与时间相关的信息。
from sklearn.model_selection import TimeSeriesSplit
xx = rs['上证综指'].copy()
_base = 252 # 1年测试样本
_max_train_sizes = [_base*1, _base*2, _base*3, _base*5]
_n_split=5
gs = gridspec.GridSpec(_n_split, len(_max_train_sizes), wspace=0.0)
fig = plt.figure(figsize=(20,25))
rows = []
for j, max_size in enumerate(_max_train_sizes):
tscv = TimeSeriesSplit(n_splits=_n_split, max_train_size=max_size)
for i, (train, test) in enumerate(tscv.split(xx)):
tmp_train = xx.iloc[train]
tmp_test = xx.iloc[test]
min_train_dt, max_train_dt = tmp_train.index.min(), tmp_train.index.max()
min_test_dt, max_test_dt = tmp_test.index.min(), tmp_test.index.max()
ks, p = stats.ks_2samp(tmp_train, tmp_test) # 获得ks检验统计指标
df_row = (max_size, ks, p,
min_train_dt.date(), max_train_dt.date(),
min_test_dt.date(), max_test_dt.date())
rows.append(df_row)
tmp_ax = plt.subplot(gs[i, j])
if i in [0,1,2,3,4] and j != 0: tmp_ax.set_yticks([])
sns.kdeplot(tmp_train, cumulative=True, lw=3, color='blue', ax=tmp_ax, label='train')
sns.kdeplot(tmp_test, cumulative=True, lw=3, color='red', ax=tmp_ax, label='test')
plt.title('max train size: {}, ks: {:.4f}, p: {:.4f}\ntrain dates: {}_{}\ntest dates: {}_{}'
.format(max_size, ks, p,
min_train_dt.date(), max_train_dt.date(),
min_test_dt.date(), max_test_dt.date()),
fontsize=11.)
plt.subplots_adjust(top=1.03)
plt.tight_layout()

从图中不难看出,在不同的回溯期间,训练样本和测试样本CDF的变化程度,包括它们准确同步的时间。为了量化我们的观察结果,可以创建一个dataframe,其中包含ks测试的输出以及回溯期和数据拆分(即训练集和测试集)的信息。
# create data table with ks test results and tss information
cols = ['max_size', 'ks', 'p', 'min_train_dt', 'max_train_dt', 'min_test_dt', 'max_test_dt']
tss_ks_df = pd.DataFrame(rows, columns=cols)
obj_cols = tss_ks_df.select_dtypes(include=['object']).columns


