决策树总结（三）剪枝

什么是剪枝？

顾名思义，剪枝就是指将决策树的某些内部节点下面的节点都删掉，留下来的内部决策节点作为叶子节点。

为什么需要剪枝？

决策树是充分考虑了所有的数据点而生成的复杂树，它在学习的过程中为了尽可能的正确的分类训练样本，不停地对结点进行划分，因此这会导致整棵树的分支过多，造成决策树很庞大。决策树过于庞大，有可能出现过拟合的情况，决策树越复杂，过拟合的程度会越高。

所以，为了避免过拟合，咱们需要对决策树进行剪枝。

一般情况下，有两种剪枝策略，分别是 预剪枝 和 后剪枝 。

下面还是通过西瓜这个例子来讲解。(还是西瓜书中的数据集)

与上面数据集不同的是，把原来的17个样本进行整理，10个样本(编号为1，2，3，6，7，10，14，15，16，17)作为训练集，7个样本(编号为4，5，8，9，11，12，13)作为测试集。( 这种留出一部分数据集作为测试集的方法作为“留出法”，西瓜书中用的就是“留出法” )

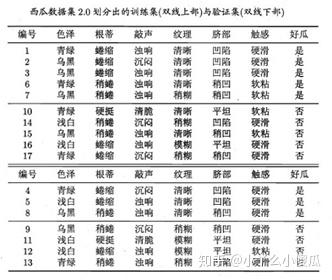
首先，先按照信息增益对这10个训练样本构造决策树，方法还是和上面的ID3算法提到的一样。

先计算最开始的训练样本的熵。好瓜有5个，坏瓜有5个，则信息熵为

Ent(D)=-(\frac{5}{10}\log_2\frac{5}{10}+\frac{5}{10}\log_2\frac{5}{10})=1\\ 再计算按照各个属性划分后的信息熵：

Ent(D_{色泽})=\frac{4}{10}\times(-\frac{2}{4}\log_2\frac{2}{4}-\frac{2}{4}\log_2\frac{2}{4})+\frac{4}{10}\times(-\frac{3}{4}\log_2\frac{3}{4}-\frac{3}{4}\log_2\frac{3}{4})\\+\frac{2}{10}\times(-1\log_21)=0.725\\

Gain(D,色泽)=1-0.725=0.275\\ 同理可得，

Gain(D,根蒂)=0.115\\Gain(D,敲声)=0.174\\Gain(D,纹理)=0.174\\Gain(D,脐部)=0.276\\Gain(D,触感)=0\\ 所以，选择脐部作为根节点。按照同样的思路，可以得到一颗为未剪枝前的决策树。

预剪枝（pre-pruning）：

预剪枝就是在构造决策树的过程中，先对每个结点在划分前进行估计，如果当前结点的划分不能带来决策树模型泛化性能的提升，则不对当前结点进行划分并且将当前结点标记为叶结点。

总结：边构造边剪枝。

如下图所示，在构造的时候就考虑到剪枝操作。

1） 首先，是否要按照“脐部”划分。在划分前，只有一个根节点，也是叶子节点，标记为“好瓜”。通过测试集验证，只有｛4，5，8｝3个样本可以正确分类，精度为 \frac{3}{7}\times100\%=42.9\% 。当按照脐部划分后，再进行验证，发现｛4，5，8，11，12｝被正确分类，精度为 \frac{5}{7}\times100\%=71.5\% 。精度提高，所以按照“脐部”进行划分。

2） 当按照脐部进行划分后，会对结点 (2) 进行划分，再次使用信息增益挑选出值最大的那个特征，信息增益值最大的那个特征是“色泽”，则使用“色泽”划分后决策树为。但是，使用“色泽”划分后，编号为｛5｝的样本会从“好瓜”被分类为“坏瓜”，只有｛4，8，11，12｝被正确分类，精确度为 \frac{4}{7}\times100\%=57.1\% 。所以，预剪枝操作会不再被这个节点进行划分。

3） 对于节点(3)，最优属性为“根蒂”。但是，这么划分后精确度仍然是 71.4\% ，所以也不会对这个节点进行操作。

预剪枝得到的决策树如下图所示。

后剪枝（post-pruning）：

后剪枝就是先把整颗决策树构造完毕，然后自底向上的对非叶结点进行考察，若将该结点对应的子树换为叶结点能够带来泛化性能的提升，则把该子树替换为叶结点。

总结：构造完再剪枝。

后剪枝算法首先考察上图中的结点 (6)，若将以其为根节点的子树删除，即相当于把结点 (6) 替换为叶结点，替换后的叶结点包括编号为{7,15}的训练样本，因此把该叶结点标记为“好瓜”（因为这里正负样本数量相等，所以随便标记一个类别），因此此时的决策树在验证集上的精度为 57.1\% （未剪枝的决策树为 42.9\% ），所以后剪枝策略决定剪枝，剪枝后的决策树如下图所示：

接着考察结点 5，同样的操作，把以其为根节点的子树替换为叶结点，替换后的叶结点包含编号为{6,7,15}的训练样本，根据“多数原则”把该叶结点标记为“好瓜”，测试的决策树精度认仍为 57.1\% ，所以不进行剪枝。

考察结点 2 ，和上述操作一样，不多说了，叶结点包含编号为{1,2,3,14}的训练样本，标记为“好瓜”，此时决策树在验证集上的精度为 71.4\% ，因此，后剪枝策略决定剪枝。剪枝后的决策树为：

接着考察结点 3 ，同样的操作，剪枝后的决策树在验证集上的精度为 71.4\% ，没有提升，因此不剪枝；对于结点 1 ，剪枝后的决策树的精度为 42.9\% ，精度下降，因此也不剪枝。

因此，基于后剪枝策略生成的最终的决策树如上图所示，其在验证集上的精度为 71.4\% 。

总结：对比预剪枝和后剪枝，能够发现，后剪枝决策树通常比预剪枝决策树保留了更多的分支，一般情形下，后剪枝决策树的欠拟合风险小，泛华性能往往也要优于预剪枝决策树。但后剪枝过程是在构建完全决策树之后进行的，并且要自底向上的对树中的所有非叶结点进行逐一考察，因此其训练时间开销要比未剪枝决策树和预剪枝决策树都大得多。

扩展：

西瓜书中的剪枝操作用的是“留出法”。总结一下剪枝的方法，内容着实很多，具体地就不展开说了。

预剪枝：

预剪枝说白了通过提前停止树的构建而对树剪枝，一旦停止，该节点就作为叶子节点了。

停止决策树生长最简单的方法有：

• 定义一个高度，当决策树达到该高度时就停止决策树的生长
• 达到某个节点的实例具有相同的特征向量，及时这些实例不属于同一类，也可以停止决策树的生长。这个方法对于处理数据的数据冲突问题比较有效。
• 定义一个阈值，当达到某个节点的实例个数小于阈值时就可以停止决策树的生长
• 定义一个阈值，通过计算每次扩张对系统性能的增益，并比较增益值与该阈值大小来决定是否停止决策树的生长。

后剪枝：

• Reduced-Error Pruning(REP,错误率降低剪枝)
• Pesimistic-Error Pruning(PEP,悲观错误剪枝)
• Cost-Complexity Pruning(CCP，代价复杂度剪枝)